李航《统计学习方法》——第八章Boosting提升方法【补充集成学习】+习题答案

Boosting与AdaBoost可视化解析

一、集成学习

  提升方法是一种常用的统计学习方法，是集成学习实现的一种方式，《统计学习方法》只介绍了提升方法的相关知识，本文从集成学习方法开始回顾，形成这部分内容的一个学习框架。
  集成学习通过构建并结合多个学习器来完成学习任务，有时也被称为多分类系统，基于委员会的学习等。

  如图所示，集成学习的一般结构是，先产生一组“个体学习器”，然后利用某种策略将他们结合起来。个体学习器通常由现有的学习算法从训练数据产生，例如C4.5决策树，BP神经网络等。图示个体学习器只包含同种类型的学习算法，这样的集成成为同质集成，此时，个体学习器成为基学习器，相应的学习算法称为基学习算法。如果集成学习包含不同的个体学习器，也就是用不同的学习算法构成个体学习器，这时称为异质集成，不再有基学习算法，个体学习器称为组件学习器。
  一般情况下将多个学习器进行结合可以获得比单一学习器更显著优越的泛化性能。但是集成效果也可能更差，因为个体分类器本身性能问题，因此为了获得好的集成，个体分类器应该“好而不同”，也就是个体学习器要有一定的准确性，并且要有多样性，保证学习器之间有差异。
  这时，集成学习涉及几个问题全部出现:

1. 如何生成个体分类器，根据其生成方式，大致可以分为两大类，即个体学习器间存在强依赖关系，必须串行生成的序列化方法(代表Boosting)，以及个体学习器间不存在强依赖关系，可同时生成的并行化方法(代表Bagging和随机森林)
2. 如何衡量个体学习器的多样性，以及如何增强多样性
3. 不同个体学习器之间如何结合，结合策略是什么
   根据西瓜书集成学习章节总结如下，具体内容参考西瓜书：
   

二、Bagging与随机森林

  欲得到泛化性能强的集成，集成中的个体学习器应尽可能相互独立，“独立“在实任务中无法做到，但是可以设法使基学习器尽可能有较大的差异—>对给定的训练数据集进行取样，产生若干个不同的子集，分别训练基学习器，集成效果较好，但是同时需要保证个体学习器的性能不能太差，如果采样的每个子集都完全不同，则每个基学习器只用到了一小部分训练数据，甚至不足以进行有效学习，因此最终使用有交叠的采样子集。
  根据样本抽取方法不同，Bagging可分为：

• 如果抽取的数据集的随机子集是样例的随机子集，我们叫做 Pasting 。
• 如果样例抽取是有放回的，我们称为 Bagging 。
• 如果抽取的数据集的随机子集是特征的随机子集，我们叫做随机子空间 (Random Subspaces)。
• 最后，如果基估计器构建在对于样本和特征抽取的子集之上时，我们叫做随机补丁 (Random Patches) 。

  最终的预测结果，在结合策略中提到了，对于分类任务使用简单投票法,即每个分类器一票进行投票(也可以进行概率平均)；对于回归任务,则采用简单平均获取最终结果,即取所有分类器的平均值。
  在多数情况下，bagging 方法提供了一种非常简单的方式来对单一模型进行改进，而无需修改背后的算法。 因为 bagging 方法可以减小过拟合，所以通常在强分类器和复杂模型上使用时表现的很好（例如，完全决策树，fully developed decision trees），相比之下 boosting 方法则在弱模型上表现更好（例如，浅层决策树，shallow decision trees）。

  随机森林，是Bagging的一个变体，在一决策树为基学习器构建Bagging集成的基础上，进一步在决策树的训练过程中引入随机属性选择。具体来说，对基决策树的每个节点，（假设有$d$个属性），先从该节点的属性集合中随机选择一个包含k个属性的子集，然后再从这个子集中选择一个最优属性用于划分，k控制了随机性的引入程度，一般情况下推荐$k=lo{g}_{2}d$。
  随机森林不仅引入了样本扰动，还引入了属性扰动，因此最终的泛化性能可以通过个体学习器之间的差异度的增加进一步提升。实现简单，计算开销小，性能强大。

三、Boosting 提升方法

3.1 提升方法的思路和提升方法AdaBoost

  在PCA框架下，一个概念是强可学习的充要条件是这个概念是弱可学习的。在学习中，找到弱可学习方法比强可学习方法容易得多，所以问题转换为如何将弱可学习方法提升为强可学习方法。大部分提升方法都是改变训练数据的概率分布（训练数据的权值分布），然后针对不同的训练数据分布调用弱学习算法学习一系列弱分类器。
  此时有两个问题：

• 在每一轮如何改变训练数据的权值或概率分布。
  【AdaBoost提高那些前一轮被弱分类器错误分类的样本的权值，降低被正确分类的样本的权值。】
• 如何将弱分类器组合成一个强分类器
  【 分类问题：加权多数表决】

AdaBoost算法：
模型：损失函数为指数函数的加法模型
学习策略：极小化加法模型的指数损失
学习算法：前向分步加法算法
输入：训练数据集$T=\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}$;弱学习算法
输出：最终分类器$G(x)$

1. 首先假设训练数据集具有均匀的权值分布$D_1=(w_{11},\cdots ,w_{1i}\cdots ,w_{1N})$,$w_{1i}=\frac{1}{N}$，即每个训练样本在基本分类器的学习中作用相同，保证第一步在原始数据上能够学习基本分类器$G_1(x)$
2. 反复学习基本分类器，假设学习$M$个基本分类器，对$m=1,2,\cdots ,M$
   (a).使用当前分布$D_m$ 加权训练数据集，学习基分类器$G_m(x)$
   (b)计算基分类器$G_m(x)$在加权训练数据集上的分类误差率：$$e_m=\sum _{i=1}^{N}P(G_m(x_i)̸=y_i)=\sum _{i=1}^N{w}_{mi}I(G_m(x_i)̸=y_i)=\sum _{G_m(x_i)̸=y_i}{w}_{mi}$$$w_{mi}$表示第$m$轮中第$i$个实例的权值，${\sum }_{i=1}^N{w}_{mi}=1$,这表明，$G_m(x)$在加权的训练数据集上的分类误差率是被$G_m(x)$误分类样本的权值之和。
   （c）计算$G_m(x)$的系数${\alpha }_m$,表示$G_m(x)$在最终分类器中的重要性。$${\alpha }_m=\frac{1}{2}ln\frac{1-e_m}{e_m}$$当$e_m\le \frac{1}{2}$时，${\alpha }_m\ge 0$,并且${\alpha }_m$随着$e_m$的减小而增大，所以分类误差率越小的基分类器在最终分类器中的作用越大。
   (d)更新训练数据集的权值分布$$\begin{gathered} D_m=(w_{m+1,1},\cdots ,w_{m+1,i},\cdots ,w_{m+1,N}) \\ {w}_{m+1,i}=\frac{w_{mi}}{Z_m}exp(-{\alpha }_m{y}_i{G}_m(x_i))=\{\begin{array}{r}\frac{w_{mi}}{Z_m}{e}^{-{\alpha }_m}{G}_m(x_i)=y_i\\ \frac{w_{mi}}{Z_m}{e}^{{\alpha }_m}{G}_m(x_i)̸=y_i\end{array} \end{gathered}$$当$e_m\le \frac{1}{2}$时，${\alpha }_m\ge 0$,所以正确分类时，样本权值被缩小，错误分类时，样本权值被增大。$Z_m$是规范因子$$Z_m=\sum _{i=1}^N{w}_{mi}exp(-{\alpha }_m{y}_i{G}_m(x_i))$$
3. 构建基本分类器的线性组合$$f(x)=\sum _{m=1}^M{\alpha }_m{G}_m(x)$$得到最终分类器为$$G(x)=sign(f(x))$$

3.2 前向分步加法模型与AdaBoost

  AdaBoost的另一种解释为：模型为加法模型，损失函数为指数函数，学习算法为前向分布算法的二分类学习算法。
  前向分布算法的目标是训练一个加法模型$f(x)={\sum }_{m=1}^M{\beta }_{m}b(x;{\gamma }_m)$,给定训练数据和损失函数，学习加法模型就变成损失函数最小化问题，通常整体优化比较复杂，所以从前向后，每一步只学习一个基函数及其系数。经过推导，AdaBoost是模型为加法模型，损失函数为指数函数，学习算法为前向分布算法的二分类学习算法。

3.3 提升树【提升树和AdaBoost的关系】

  前向分布算法+决策树（分类树or回归树）=提升树
  提升树是以分类树或者回归树为基本分类器的提升方法。分类问题用二叉分类树，回归问题用二叉回归树，最简单的回归树可看做是一个根节点连接的左右子树的二叉树，即所谓的决策树桩。提升树的模型可表示为： $$f_M(x)=\sum _{m=1}^{M}T(x;{\Theta }_m)$$$T(x;{\Theta }_m)$表示决策树，${\Theta }_m$表示决策树的参数；$M$表示树的个数。
  提升树算法采用前向分布算法，首先确定初始提升树$f_0(x)=0$，第$m$步的模型是$$f_m(x)=f_{m-1}(x)+T(x;{\Theta }_m)$$其中$f_{m-1}(x)$为当前模型，通过经验风险极小化确定下一棵决策树的参数${\Theta }_m$$${\Theta }_m=argmi{n}_{{\Theta }_m}\sum _{i=1}^{N}L(y_i,f_{m-1}(x_i)+T(x_i;{\Theta }_m))$$  针对不同的问题，提升树有不同的形式，主要区别在于损失函数不同，回归问题：平方误差损失函数；分类问题：指数损失函数；一般决策问题：一般损失函数。分类问题的提升树改变权重，回归问题的提升树拟合残差。损失函数是平方损失函数的时候，残差易求，如果不是平方损失函数也不是指数损失函数，残差就不可求，这时，就要用损失函数关于当前模型$f_{m-1}(x)$的负梯度来近似代替残差。梯度提升算法就是用梯度下降法来讲弱分类器提升为强分类器的算法。
提升树和AdaBoost之间是什么关系？
  AdaBoost是提升思想的算法模型,经典的AdaBoost一般用于分类问题，并没有指定基函数，或者说是基分类器，它可以从改变样本的权值的角度和前向分布算法的角度来解释。当确定基函数是回归或分类树时，结合前向分布算法就得出提升树算法。
  使用梯度提升进行分类的算法叫做GBDT，进行回归时则叫做GBRT。一般的提升树是用残差来确定树的叶节点的切分，并根据残差来确定该切分下的输出值，而GBDT首先是根据负梯度来确定切分，确定切分后根据线性搜索估计叶节点区域的值，使损失函数极小化。这就好比是寻找一个全局极小值，负梯度只给定一个方向，通过线性搜索确定在该方向下走几步。所以可以认为伪残差是只给出方向的残差。

3.3.1 回归提升树

  对于分类问题，只需要将上述的AdaBoost的基学习器限定为二分类树，其余的和上述的AdaBoost内容无差。对于回归问题，可看做是对输入空间$\chi$划分为J个不相交的区域，在每个区域上输出的常量为$c_j$，那么树可以表示为： $$T(x;\theta )=\sum _{j=1}^J{c}_{j}I(x\in R_j)$$其中$\theta =\{(R_1,c_1),(R_2,c_2),...,(R_J,c_J)\}$表示树的区域和区域上的常数，J表示区域的个数,是回归树的复杂度即叶结点的个数。
  对于回归树的前向分步式算法有：$$\begin{gathered} f_0(x)=0 \\ {f}_m(x)=f_{m-1}(x)+T(x;\Theta ),m=1,2,...,M \\ {f}_M(x)=\sum _{m=1}^{M}T(x;{\Theta }_m) \end{gathered}$$在前向分步式算法的第m步，给定$m-1$步的情况，需要求解：$${\theta }_m^{\ast }=arg\underset{{\Theta }_m}{\min }\sum _{i=1}^{N}L(y_i,f_{m-1}(x_i)+T(x_i;{\theta }_m)$$得到第$m$颗树的参数。
  这里我们采用平方误差拟合回归问题，则：$$L(y,f(x)=(y-f(x){)}^2$$其损失变为：$$\begin{gathered} L(y,f_{m-1}(x)+T(x;{\Theta }_m))=[y-f_{m-1}(x)-T(x:{\Theta }_m){]}^2 \\ =[r-T(x;{\Theta }_m){]}^2 \end{gathered}$$其中$r=y-f_{m-1}(x)$是当前拟合的残差，而目前我们的学习任务也仅仅是拟合这个残差,整个算法的步骤：
(1). 初始化$f_0(x)=0$
(2). 对$m=1,2\cdots ,M$
\quad\quad a. 计算残差$r=y-f_{m-1}(x)$
\quad\quad b. 拟合残差，学习一个回归树，得到$T(x;\Theta )$
\quad\quad c. 更新$f_m(x)=f_{m-1}(x)+T(x;\Theta )$
(3). 得到回归提升树$$f_M(x)=\sum _{m=1}^{M}T(x;{\Theta }_m)$$

3.3.2 梯度提升树

  前面用到的损失函数都有比较好的性质，如平方误差、指数函数等，但对于一般的函数来说，问题可能会变得复杂些，针对这一问题Freidman提出了梯度提升（Gradient Boosting），这是利用最速下降的近似方法，其关键是利用损失函数的负梯度在当前模型的值$-[\frac{\partial L(y,f(x_i))}{\partial f(x_i)}{]}_{f(x)=f_{m-1}(x)}$作为近似残差，拟合一个回归树。
算法步骤：
(1). 初始化$$f_0(x)=arg\underset{c}{\min }\sum _{i=1}^{N}L(y_i,c)$$估计使损失函数极小化的常数值，是只有一个根节点的树。
(2). 对$m=1,2\cdots ,M:$
\quad\quad a . 对于$i=1,2,...,N$, 计算$$r_{mi}=-[\frac{\partial L(y,f(x_i))}{\partial f(x_i)}{]}_{f(x)=f_{m-1}(x)}$$损失函数的负梯度在当前模型的值，将其作为残差的估计。当损失函数是平方损失函数的时候，负梯度为$2(y-f(x))|f_{m-1}(x)=2(y-f_{m-1}(x))$,文章说也就是通常所说的残差，这个2倍关系是我计算错了吗？
\quad\quad b . 拟合$r_{mi}$，学习一个回归树的叶节点区域$R_{mj},j=1,2,...,J$
\quad\quad c.对$j=1,2,...,J$计算$$c_{mj}=arg\underset{c}{\min }\sum _{x_i\in R_{mj}}L(y_i,f_{m-1}(x_i)+c)$$利用线性搜索估计叶结点区域的值，使损失函数极小化。
\quad\quad d.更新$$f_m(x)=f_{m-1}(x)+\sum _{j=1}^J{c}_{mj}I(x\in R_{mj})$$(3). 得到回归树：$$f(x{)}^{\ast }=f_M(x)=\sum _{m=1}^M\sum _{j=1}^J{c}_{mj}I(x\in R_{mj})$$

四 习题

8.1 某公司招聘支援考查身体、业务能力、发展潜力这三项。身体分为合格1、不合格0两级，业务能力和发展潜力分为上1，中2，下3三级。分类为合格1，不合格-1两类。已知10个人的数据，如下表所示，假设弱分类器为决策树桩，试用AdaBoost算法学习一个强分类器。

应聘人员情况数据表
	1	2	3	4	5	6	7	8	9	10
身体	0	0	1	1	1	0	1	1	1	0
业务	1	3	2	1	2	1	1	1	3	2
潜力	3	1	2	3	3	2	2	1	1	1
分类	-1	-1	-1	-1	-1	-1	1	1	-1	-1

from numpy import *
# adaBoost算法
# 决策树桩仅分裂一次，也就是说只选择一次特征
# 决策树桩由三部分组成，特征，特征值，不等号的方向
                               
# 读入数据
def loadData():
    dataMat = matrix([[0. , 1. , 3.],
                     [0. , 3. , 1.],
                     [1. , 2. , 2.],
                     [1. , 1. , 3.],
                     [1. , 2. , 3.],
                     [0. , 1. , 2.],
                     [1. , 1. , 2.],
                     [1. , 1. , 1.],
                     [1. , 3. , 1.],
                     [0. , 2. , 1.]])
    classLabels = matrix([-1.0, -1.0,-1.0, -1.0, -1.0, -1.0,1.0, 1.0, -1.0 , -1.0]).T
    return dataMat, classLabels


# 根据当前树桩对数据进行分类
def stumpClassify(dataMatrix, dimen, threshVal, threshIneq):
    retArray = ones((shape(dataMatrix)[0], 1))#预测矩阵
    #左叶子 ，整个矩阵的样本进行比较赋值
    if threshIneq == 'lt':
        retArray[dataMatrix[:, dimen] <= threshVal] = -1.0
    else:
        retArray[dataMatrix[:, dimen] > threshVal] = -1.0
    return retArray

'''
# 根据数据，标签和权值分布构造弱分类器，即决策树桩 stump 树桩
# D为数据权重向量
# numStep是步数，据此可算出步长， bestClassEst是最优情况下的分类情况
构造树桩要做的是： 选择合适的特征，选择合适的阈值
bestStump['dim'] 合适的特征所在维度
bestStump['thresh']  合适特征的阈值
bestStump['ineq'] 
'''
def buildStump(dataMatrix, classLabels, D):
    m, n = shape(dataMatrix)
    numStep = 10.0
    bestStump = {}  #字典
    minError = inf
    bestClasEst = mat(ones((m, 1)))
    #n是特征的种类数 
    for i in range(n):
        rangeMin = dataMatrix[:, i].min() #求每一种特征的最大最小值
        rangeMax = dataMatrix[:, i].max()
        stepSize = (rangeMax-rangeMin)/numStep
        for j in range(-1, int(numStep)+1):
            threshVal = rangeMin + j*stepSize
            #不知左树-1准确率高还是右树，因此有这样一个计算
            for inequal in ['lt', 'rt']:
                predictVals = stumpClassify(dataMatrix, i, threshVal, inequal)
                errArr = mat(ones((m, 1)))
                errArr[predictVals == classLabels] = 0
                weightedError = D.T*errArr
                if weightedError < minError:
                    minError = weightedError
                    bestClassEst = predictVals
                    bestStump['dim'] = i
                    bestStump['thresh'] = threshVal
                    bestStump['ineq'] = inequal
    return bestStump, minError, bestClassEst


# adaBoost训练过程
def adaBoostTrain(dataMatrix, classLabels, numIter=40):
    weakClassArr = []  #弱分类器
    m = shape(dataMatrix)[0]  #样本个数
    D = mat(ones((m, 1))/m)  #一开始是均值权重分布
    aggClassEst = mat(zeros((m, 1)))
    for i in range(numIter):  #numIter 弱分类器的个数
        bestStump, error, classEst = buildStump(dataMatrix, classLabels, D)
        # 防止除以零溢出
        alpha = float(0.5*log((1-error)/max(error, 1e-16)))
        bestStump['alpha'] = alpha
        weakClassArr.append(bestStump)
        expon = multiply(-1*alpha*classLabels, classEst)
        D = multiply(D, exp(expon))
        D /= D.sum()
        aggClassEst += alpha*classEst  #弱分类器结果的求和
        # 比较两个矩阵的值得出预测正误情况
        aggError = sign(aggClassEst) != classLabels
        errorRate = aggError.sum()/m
        print(errorRate)
        if errorRate == 0.0:
            break
    return weakClassArr

def adaClassify(dataMatrix, classifierArr):
    m = shape(dataMatrix)[0]
    aggClassEst = mat(zeros((m, 1)))
    for i in range(len(classifierArr)):
        stump = classifierArr[i]
        classEst = stumpClassify(dataMatrix, stump['dim'], stump['thresh'], stump['ineq'])
        aggClassEst += stump['alpha']*classEst
    return sign(aggClassEst)

dataMat, classLabels = loadData()
classifiers = adaBoostTrain(dataMat, classLabels, 9)
labels = adaClassify(mat([1,2,3]), classifiers)
print(labels)
print('dim\tthresh\tinep\talpha')
for i in range(6):
    print(str(classifiers[i]['dim'])+'\t'+str(classifiers[i]['thresh'])
          +'\t'+str(classifiers[i]['ineq'])+'\t'+str(classifiers[i]['alpha']))

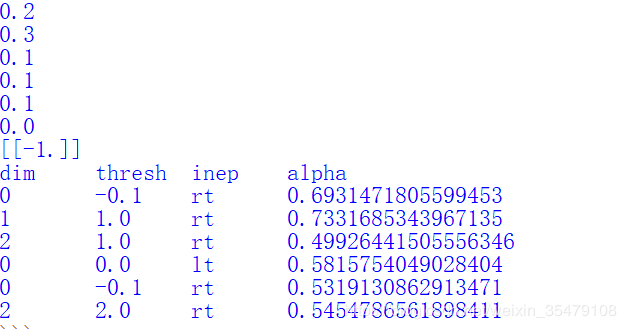
前面6行是误差率，[-1]是对第5个样本的预测，dim表示特征维度，thresh表示划分阈值，inep左树还是右树准确率高。
8.2 比较支持向量机，AdaBoost，逻辑斯蒂回归模型的学习策略与算法。

	策略	算法
支持向量机	极小化正则化合页损失，软间隔最大化	序列最小最优化（SMO）
逻辑斯蒂回归模型	极大对数似然函数，正则化的极大似然估计	改进的迭代尺度算法，梯度下降，拟牛顿
AdaBoost	极小化加法模型的指数损失	前向分步加法算法