非极大值抑制(Non-Maximum Suppression,NMS)算法与c和python代码详解

背景：非极大值抑制算法（Non-maximum suppression, NMS）的本质是搜索局部极大值，抑制非极大值元素。在目标检测之中用到非常多。

目的：搞懂此算法原理且看懂代码。

目录

一、算法解析

1.1 算法概览

1.2 算法过程

二、c代码解析

2.1 输入参量

2.2 按置信概率排序

sort函数

2.3 IOU的确定

string.compare函数

vector.at函数

2.4 概率最大框保留，重叠抑制

vector::inerator

2.5 最终保留的框

三、python代码解析

np.empty

s_sort

3.1 按照置信概率排序

numpy.argsort函数

numpy.zeros_like函数

3.2  IOU的计算

---

一、算法解析

1.1 算法概览

非极大值抑制（Non-Maximum Suppression，NMS），顾名思义就是抑制不是极大值的元素，可以理解为局部最大搜索。这个局部代表的是一个邻域，邻域有两个参数可变，一是邻域的维数，二是邻域的大小。这里不讨论通用的NMS算法(参考论文《Efficient Non-Maximum Suppression》对1维和2维数据的NMS实现)，而是用于目标检测中提取分数最高的窗口的。例如在行人检测中，滑动窗口经提取特征，经分类器分类识别后，每个窗口都会得到一个分数。但是滑动窗口会导致很多窗口与其他窗口存在包含或者大部分交叉的情况。这时就需要用到NMS来选取那些邻域里分数最高（是行人的概率最大），并且抑制那些分数低的窗口。
NMS在计算机视觉领域有着非常重要的应用，如视频目标跟踪、数据挖掘、3D重建、目标识别以及纹理分析等。

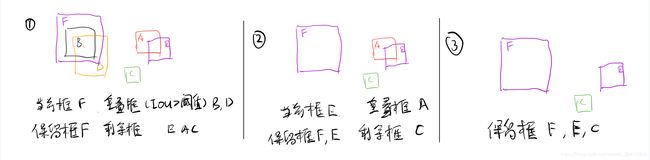
1.2 算法过程

Step1：按置信概率排列相应的备选框

Step2：取最大的框作为保留框，与其IOU大于阈值的框删除掉

Step3：剩下的框执行Step2

很容易理解

根据候选框的类别分类概率做排序：A

A

1. 先标记最大概率矩形框F是我们要保留下来的；
2. 从最大概率矩形框F开始，分别判断A~E与F的重叠度IOU（两框的交并比）是否大于某个设定的阈值，假设B、D与F的重叠度超过阈值，那么就扔掉B、D；
3. 从剩下的矩形框A、C、E中，选择概率最大的E，标记为要保留下来的，然后判读E与A、C的重叠度，扔掉重叠度超过设定阈值的矩形框

就这样一直重复下去，直到剩下的矩形框没有了，标记完所有要保留下来的矩形框

二、c代码解析

void nms(vector &boundingBox_, vector &bboxScore_, const float overlap_threshold, string modelname){
	if(boundingBox_.empty()){
        return;
    }
    std::vector heros;
    //sort the score
    sort(bboxScore_.begin(), bboxScore_.end(), cmpScore);

    int order = 0;
    float IOU = 0;
    float maxX = 0;
    float maxY = 0;
    float minX = 0;
    float minY = 0;
    while(bboxScore_.size()>0){
        order = bboxScore_.back().oriOrder;
        bboxScore_.pop_back();
        if(order<0)continue;
        heros.push_back(order);
        boundingBox_.at(order).exist = false;//delete it

        for(int num=0;numboundingBox_.at(order).x1)?boundingBox_.at(num).x1:boundingBox_.at(order).x1;
                maxY = (boundingBox_.at(num).y1>boundingBox_.at(order).y1)?boundingBox_.at(num).y1:boundingBox_.at(order).y1;
                minX = (boundingBox_.at(num).x20)?(minX-maxX+1):0;
                maxY = ((minY-maxY+1)>0)?(minY-maxY+1):0;
                //IOU reuse for the area of two bbox
                IOU = maxX * maxY;
                if(!modelname.compare("Union"))
                    IOU = IOU/(boundingBox_.at(num).area + boundingBox_.at(order).area - IOU);
                else if(!modelname.compare("Min")){
                    IOU = IOU/((boundingBox_.at(num).areaoverlap_threshold){
                    boundingBox_.at(num).exist=false;
                    for(vector::iterator it=bboxScore_.begin(); it!=bboxScore_.end();it++){
                        if((*it).oriOrder == num) {
                            (*it).oriOrder = -1;
                            break;
                        }
                    }
                }
            }
        }
    }
    for(int i=0;i

2.1 输入参量

vector &boundingBox_, 输入的备选框，Bbox类型的向量，名称为boundingBox_

struct Bbox
{
    float score;
    int x1;
    int y1;
    int x2;
    int y2;
    float area;
    bool exist;
    mydataFmt regreCoord[4];
};

其中包括四个点的坐标，置信概率，区域大小，是否存在的概率。

vector &bboxScore_, 表示框的置信概率和初始的顺序。

struct orderScore
{
    mydataFmt score;
    int oriOrder;
};

const float overlap_threshold, string modelname

分别为抑制框的IOU阈值与相应的nms的方法分为Union与Min

2.2 按置信概率排序

程序开始时，需要将相应的备选框排序

    //sort the score
    sort(bboxScore_.begin(), bboxScore_.end(), cmpScore);

与之对应的cmpScore函数为：

bool cmpScore(struct orderScore lsh, struct orderScore rsh){
    if(lsh.score

sort函数

头文件

http://www.cplusplus.com/reference/algorithm/sort/

程序意思即对备选框按照置信概率升序排列（注意这里是置信概率，置信概率之中包含了原始的备选框的位置）。

2.3 IOU的确定

maxX = (boundingBox_.at(num).x1>boundingBox_.at(order).x1)?boundingBox_.at(num).x1:boundingBox_.at(order).x1;
maxY = (boundingBox_.at(num).y1>boundingBox_.at(order).y1)?boundingBox_.at(num).y1:boundingBox_.at(order).y1;
minX = (boundingBox_.at(num).x20)?(minX-maxX+1):0;
maxY = ((minY-maxY+1)>0)?(minY-maxY+1):0;
//IOU reuse for the area of two bbox
IOU = maxX * maxY;
if(!modelname.compare("Union"))
	IOU = IOU/(boundingBox_.at(num).area + boundingBox_.at(order).area - IOU);
else if(!modelname.compare("Min")){
	IOU = IOU/((boundingBox_.at(num).area

 这部分函数相当于确定num位置和order位置的bBox之间的IOU。

string.compare函数

http://www.cplusplus.com/reference/string/string/compare/

string在c与python之中都有出现且常用，所以应当仔细研读，熟练运用。

返回值为0表示相等。modelname.compare("Union")表示modelname为 "Union"时候则返回0.

vector.at函数

http://www.cplusplus.com/reference/vector/vector/at/

  std::vector myvector (10);   // 10 zero-initialized ints

  // assign some values:
  for (unsigned i=0; i

2.4 概率最大框保留，重叠抑制

    while(bboxScore_.size()>0){
        order = bboxScore_.back().oriOrder;
        bboxScore_.pop_back();
        if(order<0)continue;
        heros.push_back(order);
        boundingBox_.at(order).exist = false;//delete it

概率最大的框的在Bbox向量组中的序列存于order之中，存于向量hero之中，然后当前boundingBox删掉，其exist设为false

if(IOU>overlap_threshold){
	boundingBox_.at(num).exist=false;
	for(vector::iterator it=bboxScore_.begin(); it!=bboxScore_.end();it++){
		if((*it).oriOrder == num) {
			(*it).oriOrder = -1;
			break;
		}
	}
}

与最大概率框IOU大于阈值的框也删掉。首先是boundingBox的exist设为false，然后bboxScore的oriOrder设为-1

vector::inerator

http://www.cplusplus.com/reference/vector/vector/

2.5 最终保留的框

    for(int i=0;i

只是将最终保留的框的exist设为true，删掉的框exist设为false，但是其内存空间还是占用的。

三、python代码解析

def nms(boxes, threshold, method):
    if boxes.size == 0:
        return np.empty((0, 3))
    x1 = boxes[:, 0]
    y1 = boxes[:, 1]
    x2 = boxes[:, 2]
    y2 = boxes[:, 3]
    s = boxes[:, 4]
    area = (x2 - x1 + 1) * (y2 - y1 + 1)
    s_sort = np.argsort(s)
    pick = np.zeros_like(s, dtype=np.int16)
    counter = 0
    while s_sort.size > 0:
        i = s_sort[-1]
        pick[counter] = i
        counter += 1
        idx = s_sort[0:-1]
        xx1 = np.maximum(x1[i], x1[idx])
        yy1 = np.maximum(y1[i], y1[idx])
        xx2 = np.minimum(x2[i], x2[idx])
        yy2 = np.minimum(y2[i], y2[idx])
        w = np.maximum(0.0, xx2 - xx1 + 1)
        h = np.maximum(0.0, yy2 - yy1 + 1)
        inter = w * h
        if method is 'Min':
            o = inter / np.minimum(area[i], area[idx])
        else:
            o = inter / (area[i] + area[idx] - inter)
        s_sort = s_sort[np.where(o <= threshold)]
    pick = pick[0:counter]
    return pick

np.empty

https://docs.scipy.org/doc/numpy/reference/generated/numpy.empty.html

https://blog.csdn.net/HHTNAN/article/details/78590780

    if boxes.size == 0:
        return np.empty((0, 3))

这个表示若是没有输入相应的框则返回空数组，数组中带0则数组不存在，输出为空 []

s_sort

https://blog.csdn.net/HARDBIRD123/article/details/82261651

3.1 按照置信概率排序

def nms(boxes, threshold, method):
    if boxes.size == 0:
        return np.empty((0, 3))
    x1 = boxes[:, 0]
    y1 = boxes[:, 1]
    x2 = boxes[:, 2]
    y2 = boxes[:, 3]
    s = boxes[:, 4]
    area = (x2 - x1 + 1) * (y2 - y1 + 1)
    s_sort = np.argsort(s)
    pick = np.zeros_like(s, dtype=np.int16)
    counter = 0

这部分代码计算了相应的区域的面积，然后运用numpy.argsort函数对置信概率进行排序。

numpy.argsort函数

https://docs.scipy.org/doc/numpy/reference/generated/numpy.argsort.html

针对s排序的顺序存在s_sort数组之中。

numpy.zeros_like函数

https://docs.scipy.org/doc/numpy/reference/generated/numpy.zeros_like.html

返回一个与初始置信概率数组相同结构的数组 s=boxes[:,4]，(这里数据类型为int16)。pick为最终选用的置信概率。

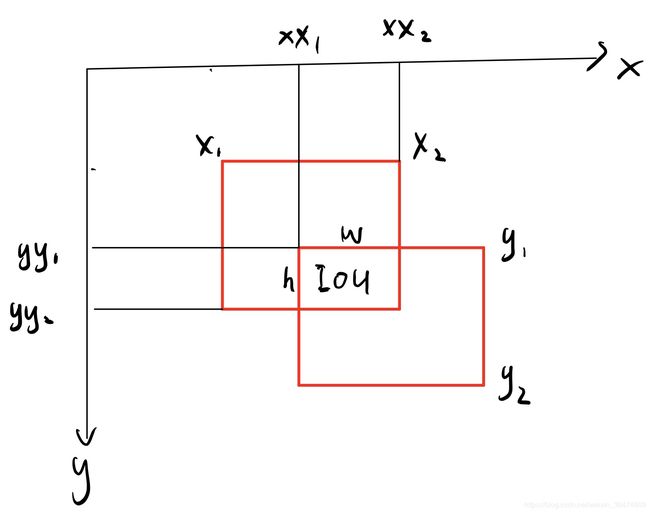
3.2  IOU的计算

    while s_sort.size > 0:
        i = s_sort[-1]
        pick[counter] = i
        counter += 1
        idx = s_sort[0:-1]
        xx1 = np.maximum(x1[i], x1[idx])
        yy1 = np.maximum(y1[i], y1[idx])
        xx2 = np.minimum(x2[i], x2[idx])
        yy2 = np.minimum(y2[i], y2[idx])
        w = np.maximum(0.0, xx2 - xx1 + 1)
        h = np.maximum(0.0, yy2 - yy1 + 1)
        inter = w * h
        if method is 'Min':
            o = inter / np.minimum(area[i], area[idx])
        else:
            o = inter / (area[i] + area[idx] - inter)
        s_sort = s_sort[np.where(o <= threshold)]