cs224笔记: Lecture 4 Backpropagation and Computation Graph

Backpropagation and Computation Graph

1. Derivative w.r.t. a weight matrix

还是之前的那个例子，应用chain rule求解梯度，前向计算式子如下:
$$\begin{gathered} s={\mathbf{u}}^T\mathbf{h} \\ \mathbf{h}=f(\mathbf{z}) \\ \mathbf{z}=\mathbf{W}\mathbf{x}+\mathbf{b} \end{gathered}$$
其中$\mathbf{W}$是$n\times m$，$s$是一个标量。
$$\frac{\partial s}{\partial \mathbf{W}}=\frac{\partial s}{\partial \mathbf{h}}\frac{\partial \mathbf{h}}{\partial \mathbf{z}}\frac{\partial \mathbf{z}}{\partial \mathbf{W}}$$
反向传播，用到之前求过的导数，令$\delta =\frac{\partial s}{\partial \mathbf{z}}=\frac{\partial s}{\partial \mathbf{h}}\frac{\partial \mathbf{h}}{\partial \mathbf{z}}$，$\delta (n,1)$展开如下：
$$\delta =[\frac{\partial s}{\partial z_1},...,\frac{\partial s}{\partial z_n}]$$
则应用chain rule：
$$\frac{\partial s}{\partial \mathbf{W}}=\delta \frac{\partial \mathbf{z}}{\partial \mathbf{W}}=\delta \frac{\partial }{\partial \mathbf{W}}(\mathbf{W}\mathbf{x}+\mathbf{b})$$
考虑$\mathbf{z}$对$\mathbf{W}$的偏导求解：
$$\begin{array}{rl}\frac{\partial z_i}{\partial W_{ij}}& =\frac{\partial }{\partial W_{ij}}(W_{i}x+b_i)\\ & =\frac{\partial }{\partial W_{ij}}\sum _{k=1}^d{W}_{ik}{x}_k\\ & =x_j\end{array}$$
代入原式有(${\delta }_i$对应$z_i$，$z_i$对应$x_j$):
$$\frac{\partial s}{\partial W_{ij}}={\delta }_i{x}_j$$
所以总的结果是一个外积(outer product):
$$\begin{gathered} \frac{\partial s}{\partial \mathbf{W}}={\delta }^T{\mathbf{x}}^T \\ (n,m)=(n,1)\times (1,m) \end{gathered}$$

Pitfall问题

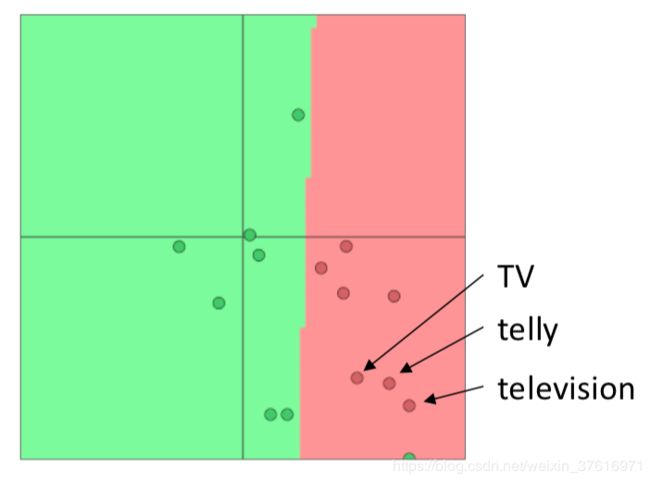
假设我们使用预训练好的词向量做训练，有三个同义单词：TV，telly，television，但是前两个在训练集中，第三个在测试集中，这样本身预训练好的三个词向量在相近的区间，但是在我们的训练集一顿操作后，前两个词向量位置改变了，变得与第三个远了，这样就给后来的任务带来了麻烦，例如分类任务，同义的三个词有可能会被分成两类。上图：

(训练前，拿到别人训练好的词向量)

(跑完我们的训练后)

解决方法：
If you only have a small training data set, don’t train the word vectors；
If you have have a large dataset, it probably will work better to “train = update = fine-tune” word vectors to the task；

大意就是如果你的训练集比较小，就直接拿别人训练好的词向量用就完事了，不要再用你的数据集训练了，很容易出现上述的pitfall问题；但是你如果有一个很大的训练集，那可以再对训练后的词向量做fine-tuning，而不太可能出现pitfall的问题

2. Computation Graphs and Backpropagation

引入计算图(Computation Graphs)，便于我们对神经网络前向传播后向传播的理解和计算。

还是上个例子：
$$\begin{gathered} s={\mathbf{u}}^T\mathbf{h} \\ \mathbf{h}=f(\mathbf{z}) \\ \mathbf{z}=\mathbf{W}\mathbf{x}+\mathbf{b} \\ \mathbf{x}(inputs) \end{gathered}$$
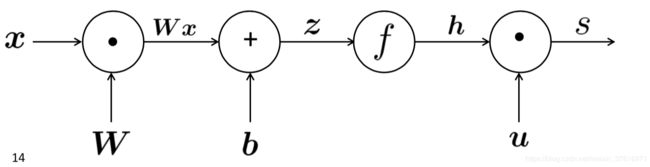
前向传播(forward progagation) 的计算图如下：

源点为输入，中间结点是操作(operations)，边(edges)传递操作的结果。

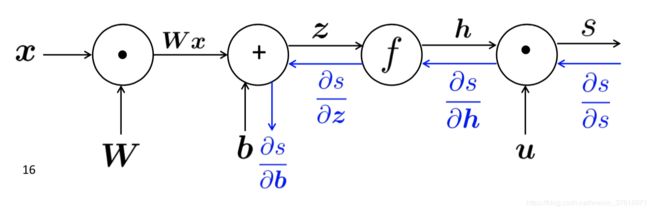
反向传播(backpropagation) 计算图如下，边(edges)传递梯度：

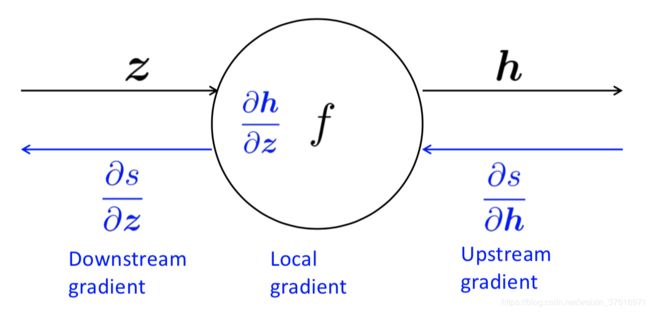
对于每一个结点都会存储一个局部梯度(local gradient)，便于反向传播梯度的计算：

有了local gradient，应用chain rule计算梯度如下：
$$\frac{\partial s}{\partial \mathbf{z}}=\frac{\partial s}{\partial \mathbf{h}}\frac{\partial \mathbf{h}}{\partial \mathbf{z}}$$

$$[DownstreamGradient]=[UpstreamGradient]\times [LocalGradient]$$

举个例子，函数及输入如下：
$$\begin{gathered} f(x,y,z)=(x+y)max(y,z) \\ x=1,y=2,z=0 \end{gathered}$$
前向传播步骤如下:
$$\begin{gathered} a=x+y \\ b=max(y,z) \\ f=ab \end{gathered}$$

计算local gradients并存储在各结点：
$$\begin{gathered} \frac{\partial a}{\partial x}=1 \\ \frac{\partial a}{\partial y}=1 \\ \frac{\partial b}{\partial y}=1 \\ \frac{\partial b}{\partial z}=0 \\ \frac{\partial y}{\partial a}=b=2 \\ \frac{\partial y}{\partial b}=a=3 \end{gathered}$$
反向传播计算梯度，downstream=upstream*local：
$$\begin{gathered} \frac{\partial f}{\partial f}=1 \\ \frac{\partial f}{\partial a}=\frac{\partial f}{\partial f}\frac{\partial f}{\partial a}=1\ast 2=2 \\ \frac{\partial f}{\partial b}=\frac{\partial f}{\partial f}\frac{\partial f}{\partial b}=1\ast 3=2 \\ \frac{\partial f}{\partial x}=\frac{\partial f}{\partial a}\frac{\partial a}{\partial x}=2\ast 1=2 \\ \frac{\partial f}{\partial y}=\frac{\partial f}{\partial a}\frac{\partial a}{\partial y}+\frac{\partial f}{\partial b}\frac{\partial b}{\partial y}=2\ast 1+3\ast 1=5 \\ \frac{\partial f}{\partial z}=\frac{\partial f}{\partial b}\frac{\partial b}{\partial z}=2\ast 0=0 \end{gathered}$$

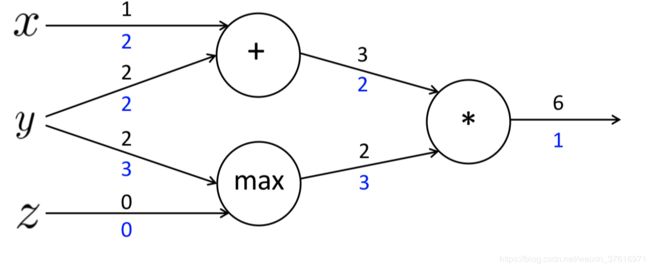
这里注意$y$的upstream来自两部分$a$和$b$，在计算$y$的梯度时需要将它们加起来。计算图如下，蓝色数字字代表反向传播的梯度

In General

1 前向传播：

-按照拓扑结构的顺序(topological sort order)访问结点

-在给定前驱结点值的基础上计算结点的值

2 反向传播

-初始化输出的梯度为1

-以拓扑逆序访问每个结点，使用后继结点的梯度应用chain rule计算当前结点的梯度

（这里计算图肯定是无环图(acyclic graph)，所以拓扑顺序很好确定）

通过数值计算梯度可以用于检验梯度

例如定义一个较小的$h=1e-4$，导数可以通过$f^{\prime }(x)=\frac{f(x+h)-f(x-h)}{2h}$得到一个近似值

这个方法易于实现，但是计算比较耗时。

3. Regularizations/Vectorization/Non-linearities/Parameters Initialization/Optimizers/Learning Rate

Regularization(正则化)

奥卡姆剃刀原则，我们希望训练出的模型越简单越好，所以在损失函数里对参数增加了一个惩罚项，可以解决过拟合(overfitting)问题

例如对所有参数增加一个L2 Regularization：
$$J(\theta )=\frac{1}{N}-\log (\frac{exp(f_{y_i})}{{\sum }_{c=1}^{C}exp(f_{y_c})})+\lambda \sum _k{\theta }_k^2$$

Vectorization

使用向量(矩阵)表示数据，进行计算可以大大加快算法的速度。

Non-linearities

logistic(“sigmoid”)
$$f(z)=\frac{1}{1+exp(-z)}$$
tanh，其实可以由logistic转换得到，$tanh(z)=2logistic(2z)-1$
$$f(z)=\frac{exp(z)-exp(-z)}{exp(z)+exp(-z)}$$
hard tanh:
$$HardTanh(z)=\{\begin{array}{ll}-1& \text{if x<-1}\\ x& \text{if -1<=x<=1}\\ 1& \text{if x>1}\end{array}$$
上述的logistic和tanh如今只有一些特殊的情况下使用，深度网络不在用到它们。

ReLU(rectified linear unit)
$$rect(z)=max(z,0)$$
Leaky ReLU
$$leakyReLU(z)=\{\begin{array}{ll}0.01x& \text{if x<0}\\ x& \text{if x>=0}\end{array}$$
ReLU会经常用于构造feed-forward深度网络，训练快性能好。

Parameters Initialization

参数通常是用一个随机的小的数字初始化，为了避免相同防止其阻碍训练(To avoid symmetries that prevent learning/specialization)

Optimizers

通常SGD就可以，其他的如: Adagrad, RMSprop, Adam, SparseAdam

Learning Rates

可以使用一个常量作为学习率，但是它的大小必须小心定义，过大会导致模型不能收敛，过小会导致模型收敛时间过长。

也可以通过学习时间到增长不断得减少学习率，可以手动的凭经验去调整，也可以通过一些公式自动调整，例如
$$lr=l{r}_0{e}^{-kt},\text{for epoch t}$$