ADMM
背景知识
对偶上升
等式约束优化问题:
![]()
f f f是凸函数,2.1的拉格朗日项为:
![]()
其对偶函数为:
![]()
inf代表下确界,之所以用下确界而不是用min,可能是因为有些函数没有极值(定义域取不到),但有一个下确界。
y是拉格朗日乘子项的对偶变量
则原问题的对偶问题变为:
![]()
在强凸性质下,原问题和对偶问题的最优解是一样的。
我们可以从对偶的最优点 y ∗ y^* y∗恢复出原优化问题的最优点 x ∗ x^* x∗:
![]()
利用梯度上升法:
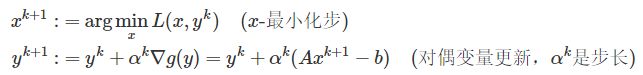
上述条件很严苛,
- f ( x ) f(x) f(x)要求严格凸,并且 α \alpha α选择要比较合适,一般应用中都不会满足。因此对偶上升不会直接应用。
对偶分解:
尽管对偶上升的条件很严苛,但是它有时写成并行算法,当目标函数 f f f是可分离的时候:

x = ( x 1 , x 2 , . . . . , x N ) x=(x_1,x_2,....,x_N) x=(x1,x2,....,xN)并且矩阵A可以分解为 A = [ A 1 , . . . A N ] A=[A_1,...A_N] A=[A1,...AN] ,
A x = ∑ i = 1 N A i x i Ax=\sum_{i=1}^{N}A_ix_i Ax=∑i=1NAixi
故拉格朗日项可以写成:

因此迭代优化的时候, m i n x min_x minx可以拆成多个问题的并行优化,对偶变量更新不变这对于参数特别多的特别有用。

增广拉格朗日和乘子法
增广拉格朗日方法 是在罚函数的基础上增加了拉格朗日乘子项,故称为增广拉格朗日函数。
其放松了 f ( x ) f(x) f(x)严格凸的假设和一些其它条件,同时使得算法更加稳健。2.1的问题变为:
![]()
等价于
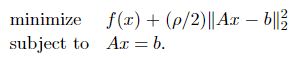
惩罚项的好处是使得对偶函数
![]()
在更一般的条件下可导:
增广拉格朗日相比于对偶上升多了一个平方项,但这个平方项无法分离,使得不能利用对偶上升的分块思想并行优化。所以针对此的改进,ADMM算法诞生了。
ADMM
为了整合对偶上升的可分解性和增广拉格朗日法(也叫乘子罚函数法)优秀的收敛性质,ADMM(Alternating Direction of Method of Multipliers)结合了两者的优点,
最开始(2.1)的优化问题可以写为:
![]()
于是:![]()
对偶分解的时候 x = ( x 1 , x 2 , . . . . , x N ) x=(x_1,x_2,....,x_N) x=(x1,x2,....,xN),在二次项里面不能被写成分块的形式,但在这里x被分成了x和z,天生分块,并且z作为一个独立变量不需要融合进x,保证了过程的可分解性。
于是:
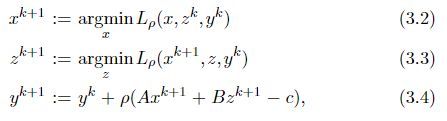
ADMM算法包括了除x以外的 ( z k + 1 , y k + 1 ) (z^{k+1},y^{k+1}) (zk+1,yk+1),它是 ( z k , y k ) (z^{k},y^{k}) (zk,yk)的函数,x并不在其中。
scaled Form—简化ADMM
令残差 r = A x + B z − c , u = ( 1 / ρ ) ∗ y r=Ax+Bz-c,u=(1/\rho) *y r=Ax+Bz−c,u=(1/ρ)∗y,增广拉格朗日项的线性项和二次项可以写成:
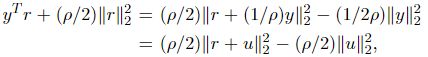
于是简化后的ADMM:常数项可以忽略
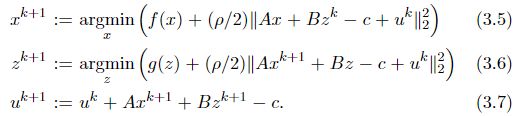
每次迭代时残差 r k = A x k + B z k − c r^{k}=Ax^{k}+Bz^{k}-c rk=Axk+Bzk−c,故
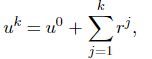
ADMM的具体应用
约束凸优化问题
一般受约束的凸优化问题可以写成如下形式:
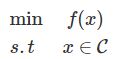
f f f为凸函数, C C C为凸集
增加分离变量,写成ADMM形式:
![]()
g g g是z的指示函数,即在 x ∈ C x\in C x∈C时有值;
其增广拉格朗日为:
![]()
ADMM的缩放形式:
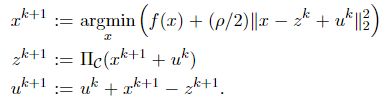
这里的z的形式可以通过求导取极值点得到。
一般的l1损失函数
更为一般的优化模型:
![]()
l l l为凸损失函数
写成ADMM可以使用的形式:
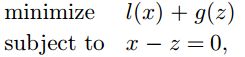
其中, g ( z ) = λ ∣ ∣ z ∣ ∣ 1 g(z)=\lambda ||z||_1 g(z)=λ∣∣z∣∣1
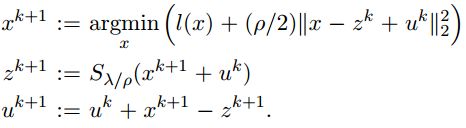
x − u p d a t e x-update x−update是proximal operator evaluation,如果 l l l是平滑的,则可以用牛顿法、拟牛顿法(quasi Newton method)、共轭梯度法来解决,如果 l l l是二次项,x-min 能够直接解线性方程组。
Lasso
L1正则线性回归也叫Lasso, l ( x ) = ( 1 / 2 ) ∣ ∣ A x − b ∣ ∣ 2 2 l(x)=(1/2)||Ax-b||_2^2 l(x)=(1/2)∣∣Ax−b∣∣22,
这里的l就是二次项,我们尝试着解解方程
![]()
ADMM形式:
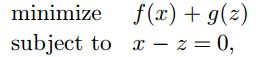
f ( x ) = ( 1 / 2 ) ∣ ∣ A x − b ∣ ∣ 2 2 f(x)=(1/2)||Ax-b||_2^2 f(x)=(1/2)∣∣Ax−b∣∣22, g ( z ) = λ ∣ ∣ z ∣ ∣ 1 g(z)=\lambda ||z||_1 g(z)=λ∣∣z∣∣1
根据上面的scaled-form形式,可以推出:
x k + 1 = a r g m i n x ( 1 / 2 ) ∣ ∣ A x − b ∣ ∣ 2 2 + ρ 2 ∣ ∣ x − z ( k ) + u ( k ) ∣ ∣ 2 2 z ( k + 1 ) = a r g m i n z λ ∣ ∣ z ∣ ∣ 1 + ρ 2 ∣ ∣ x k − z + u ( k ) ∣ ∣ 2 2 u ( k = 1 ) = u ( k ) + x k − z ( k ) x^{k+1}=argmin_x (1/2)||Ax-b||_2^2+\frac{\rho}{2}||x-z^{(k)}+u^{(k)}||_2^2 \\ z^{(k+1)}=argmin_z\lambda ||z||_1+\frac{\rho}{2}||x^{k}-z+u^{(k)}||_2^2\\ u^{(k=1)}=u^{(k)}+x^{k}-z^{(k)} xk+1=argminx(1/2)∣∣Ax−b∣∣22+2ρ∣∣x−z(k)+u(k)∣∣22z(k+1)=argminzλ∣∣z∣∣1+2ρ∣∣xk−z+u(k)∣∣22u(k=1)=u(k)+xk−z(k)
对x的更新求导取零:
A T ( A x − b ) + ρ ( x − z k + u k ) = 0 ( A T A + ρ I ) x − ( A T b + ρ ( z k − u k ) ) = 0 x k + 1 = ( A T A + ρ I ) − 1 ( A T b + ρ ( z k − u k ) ) A^T(Ax-b)+\rho (x-z^{k}+u^{k})=0 \\ (A^TA+\rho I)x-(A^Tb+\rho (z^{k}-u^{k}))=0\\ x^{k+1} =(A^TA+\rho I)^-1(A^Tb+\rho (z^{k}-u^{k})) AT(Ax−b)+ρ(x−zk+uk)=0(ATA+ρI)x−(ATb+ρ(zk−uk))=0xk+1=(ATA+ρI)−1(ATb+ρ(zk−uk))
z z z的更新用上面的subgradient引入的soft thresholding:
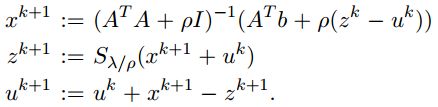
注意 A T A + ρ I A^TA+\rho I ATA+ρI总是可逆的,since ρ > 0 \rho >0 ρ>0.
这里的矩阵可以可以作一些分解使得迭代收敛更快,详情见[4]。
x-update exploit
在x变量更新时,里面的 f , g , A , B f,g,A,B f,g,A,B涉及到矩阵的运算,涉及到大量的数据时,迭代的速度会变得缓慢,因此,对x-update的开发求解很重要。
简化x-update的分析:
![]()
尽管z是一个变量,但在x迭代中是一个常量,因此 v = − B z + c − u v= -Bz+c-u v=−Bz+c−u当作一个常量即可。
Proximity Operator 近端(临近)算子
再次简化 A = I A=I A=I,
![]()
作为 v v v的函数,右边的项也被定义为 p r o x f , ρ ( v ) prox_{f,\rho}(v) proxf,ρ(v),被称为带惩罚项 ρ \rho ρ的f的近端算子。
在变分分析中,以f的Moreau envelope or Moreau-Yosida regularization的而出名。并且与the proximal point algorithm有关系

近端算子里的x-min也被称为近端优化。
尽管这不会对我们的ADMM加快效率,但是当f足够简单时,我们可以更方便的分析x-update,比如f是一个闭合非空凸集C的指示函数:
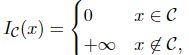
f的近端算子就退化为一个C上的欧几里得距离:
![]()
因此,近端运算符可以被视为广义投影。f的近端算子也可以被解释为f的一种梯度。
(就像上面的约束凸优化问题一样)
![]()
从这个式子可以理解,式在寻找一个距离v点不要太远的x点,然后使得 f ( x ) f(x) f(x)最小。
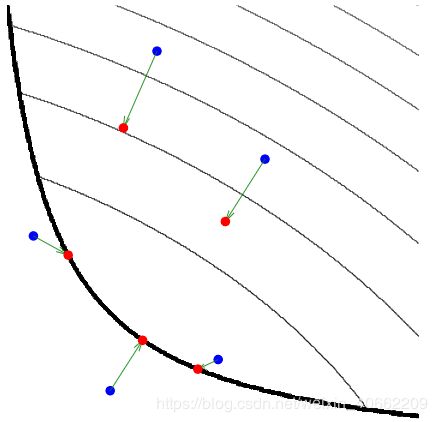
为什么要使用近端算子
如果目标函数式处处可微的,那么直接用梯度下降法即可,但更多的情况时f不可微的,通常这种情况下使用次梯度来优化,但是次梯度的缺点时求解慢和通常不会产生稀疏解。
近端算子则是在 f ( x ) f(x) f(x)分解为一个可微分的凸函数和不可微分的凸函数的条件下:
f ( x ) = g ( x ) + h ( x ) f(x) = g(x)+h(x) f(x)=g(x)+h(x)
Proximal Algorithm 自然肩负了要解决这两个问题的使命。
其中函数f可能是非光滑(即不可微)的。临近算子是对梯度的延伸,当函数f为光滑函数时,该临近算子就是梯度。
soft thresholding
soft thresholding就是1范数的近端算子;
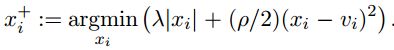
![]()
S就是所谓的软阈值算子:就是上
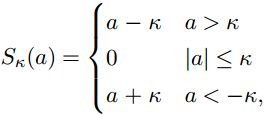
特别感谢:
- 高涛—分布式计算、统计学习与ADMM算法
- Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Stephen Boyd. 2011
- 吴良超–最优化计算课程总结
- Fast Image Recovery Using Variable Splitting and Constrained Optimization. Manya V. Afonso. 2010
- Proximal Algorithm 入门 https://blog.csdn.net/luoleicn/article/details/52676378
- 近端梯度法(Proximal Gradient Method, PG) https://blog.csdn.net/qq547276542/article/details/78251779
- 近端梯度法(Proximal Gradient Descent https://blog.csdn.net/zbwgycm/article/details/83060251