_leon1999
_leon1999

对抗搜索（极大极小值搜索）

http://web.cs.ucla.edu/~rosen/161/notes/alphabeta.html

http://web.cs.ucla.edu/~rosen/161/notes/minimax.html

读完上边的文章之后应该就差不多了。

附上学长给的图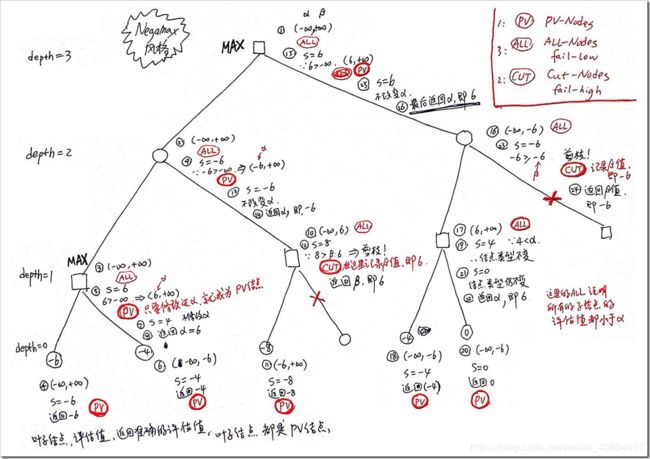对抗搜索（极大极小值搜索）_第1张图片

对抗搜索（极大极小值搜索）_第2张图片

这两张就是伪代码和搜索的过程。

在这里记录一下我的理解：这个搜索过程是在一颗决策树上进行的，两方我们分别记为max 和min 。

当轮到max进行操作时我们希望我们子情况的值尽可能大，当到min操作时我们希望子情况的值尽可能小。

这就是极大极小原理，但是这样的话时间复杂度依旧很高，我们就需要加上α-β剪枝优化

剪枝的原理也很简单，

例如：如果父节点是max操作  其中已经求出来的一个值是4 现在轮到min进行操作，如果我们找到min的一个子情况的值是3

我们就不再需要去找当前min的其他子节点了。 以为当前是求一个最小的 3 已经足够说明此节点（min）对上一步的max

操作没有贡献。

这里记录一下辉神讲过的一道题，我只重写了搜索的过程 ，判断函数直接是用辉神的。就是节点判断横竖和对角够不够4个

其中搜索的过程写法比较多。

分开写 合起来写 负值最大等

但是我感觉按照上图的伪代码的过程写比较好理解,也很好写。

poj 1568

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
#define rep(i,j,k) for(int i=j;i<=k;i++)
#define sca(x) scanf("%d",&x)
#define pb(x) push_back(x)
#define per(i,j,k) for(int i=j;i>=k;i--)
#define inf 0x3f3f3f3f
#define LL long long
#define N 10005
#define MAXN 2000005
#define inf 0x3f3f3f3

int xx,yy;
char a[10][10];
int evalue()
{
     int i,j,z,zz,zt,zzt;
    for(i=0; i<4; i++)
    {
        z=0,zz=0,zt=0,zzt=0;
        for(j=0; j<4; j++)
        {
            if(a[i][j]=='x')
                z++;
            else if(a[i][j]=='o')
                zz++;
            if(a[j][i]=='x')
                zt++;
            else if(a[j][i]=='o')
                zzt++;
        }
        if(z==4||zt==4)
            return 1;
        if(zz==4||zzt==4)
            return -1;
    }
    zt=0,zzt=0,z=0,zz=0;
    for(i=0; i<4; i++)
    {
        if(a[i][i]=='x')
            z++;
        if(a[i][i]=='o')
            zz++;
        if(a[i][3-i]=='x')
            zt++;
        if(a[i][3-i]=='o')
            zzt++;
    }
    if(z==4||zt==4)
        return 1;
    if(zz==4||zzt==4)
        return -1;
    return 0;
}

int minimax(int dep,int now,int alp,int bet)
{
    int flag=evalue();
    if(flag||dep==0)
        return flag;
    if(now)
    {
        int val=-1;
        for(int i=0;i<4;i++)
        {
            for(int j=0;j<4;j++)
            {
                if(a[i][j]=='.')
                {
                    a[i][j]='x';
                    val=max(val,minimax(dep-1,!now,alp,bet));
                    a[i][j]='.';
                    if(val>=alp)alp=val;
                    if(alp>=bet) //记录我下的第一个必胜点的坐标。
                    {
                        xx=i,yy=j;
                        return alp;
                    }
                }
            }
        }
        return alp;
    }
    else
    {
        int val=1;
        for(int i=0;i<4;i++)
        {
            for(int j=0;j<4;j++)
            {
                if(a[i][j]=='.')
                {
                    a[i][j]='o';
                    val=min(val,minimax(dep-1,!now,alp,bet));
                    a[i][j]='.';
                    if(val<=bet)bet=val;
                    if(bet<=alp)return bet;
                }
            }
        }
        return bet;
    }
}
int main()
{
    char cc;
    while(~scanf("%c",&cc))
    {
        if(cc=='$')break;
        char ch=getchar();
        int sum=0;
        rep(i,0,3)
        {
            scanf("%s",a[i]);
            rep(j,0,3)
            {
                if(a[i][j]=='x')sum++;
            }
        }
        sum*=2;
        if(sum<=4)printf("#####\n");
        else
        {
            if(minimax(16-sum,1,-1,1))
                printf("(%d,%d)\n",xx,yy);
            else printf("#####\n");
        }
        ch=getchar();
    }
}

参考博客：

https://blog.csdn.net/u013351484/article/details/50789521

你可能感兴趣的:(对抗搜索)

  • QQ群采集助手，精准引流必备神器 2401_87347160 其他经验分享
    功能概述微信群查找与筛选工具是一款专为微信用户设计的辅助工具，它通过关键词搜索功能，帮助用户快速找到相关的微信群，并提供筛选是否需要验证的群组的功能。主要功能关键词搜索：用户可以输入关键词，工具将自动查找包含该关键词的微信群。筛选功能：工具提供筛选机制，用户可以选择是否只显示需要验证或不需要验证的群组。精准引流：通过上述功能，用户可以更精准地找到目标群组，进行有效的引流操作。3.设备需求该工具可以
  • 使用Faiss进行高效相似度搜索 llzwxh888 faisspython
    在现代AI应用中，快速和高效的相似度搜索是至关重要的。Faiss（FacebookAISimilaritySearch）是一个专门用于快速相似度搜索和聚类的库，特别适用于高维向量。本文将介绍如何使用Faiss来进行相似度搜索，并结合Python代码演示其基本用法。什么是Faiss？Faiss是一个由FacebookAIResearch团队开发的开源库，主要用于高维向量的相似性搜索和聚类。Faiss
  • Faiss Tips：高效向量搜索与聚类的利器 焦习娜Samantha
    FaissTips：高效向量搜索与聚类的利器faiss_tipsSomeusefultipsforfaiss项目地址:https://gitcode.com/gh_mirrors/fa/faiss_tips项目介绍Faiss是由FacebookAIResearch开发的一个用于高效相似性搜索和密集向量聚类的库。它支持多种硬件平台，包括CPU和GPU，能够在海量数据集上实现快速的近似最近邻搜索（AN
  • 心有蓝天白云，爱情便会晴空万里，然后有花香有鸟鸣有美好的未来 曹十二吖
    丁南的婚姻，来自于一场她对生命的对比。她曾经说过，当她最爱的母亲用生命去逼迫她结婚的时候，她曾一度不理解到愤怒，甚至于想过用轻生来对抗母亲的不理智。庆幸的是，丁南是一个自我调节能力非常强的人，她想如果我连死亡都不怕，还怕不能经营好一段婚姻吗？抱着这样的念头，24年没有谈过恋爱的她，用短短三个月的时间，完成了少女到女人的蜕变。她曾经说过：“我要把自己最珍贵的东西留给自己命中注定的那个人。”闺蜜几人中
  • Faiss：高效相似性搜索与聚类的利器 网络·魚 大数据faiss
    Faiss是一个针对大规模向量集合的相似性搜索库，由FacebookAIResearch开发。它提供了一系列高效的算法和数据结构，用于加速向量之间的相似性搜索，特别是在大规模数据集上。本文将介绍Faiss的原理、核心功能以及如何在实际项目中使用它。Faiss原理：近似最近邻搜索：Faiss的核心功能之一是近似最近邻搜索，它能够高效地在大规模数据集中找到与给定查询向量最相似的向量。这种搜索是近似的，
  • 容易满足的小孩 洒在心头的阳光
    去年买的榨汁机没有用几次就坏了，前些时间答应娃儿给他买个，天天没事就问我，啥时候买，还自己淘宝上比较，加入购物车，这不前几天赶紧给他买了，省的每天叨叨在我耳边念叨着。今天终于到货了，因为他一直想和喝芒果汁，顺便买了芒果在家，放学回来兴奋的，赶紧要榨芒果汁，还特意搜索一下芒果汁的做法，我说他要是学习能有吃这般如此认真，我也就没有那么操心了。今晚喝到了芒果汁，他很开心，是阿，孩子就是这么容易满足，得到
  • 母亲节如何做小红书营销 美橙传媒
    小红书的一举一动引起了外界的高度关注。通过爆款笔记和流行话题，我们可以看到“干货”类型的内容在小红书中偏向实用的生活经验共享和生活指南非常受欢迎。根据运营社的分析，这种现象是由小红书用户心智和内容社区背后机制共同决定的。首先，小红书将使用“强搜索”逻辑为用户提供特定的“搜索场景”。在“我必须这样生活”中，大量使用了满足小红书站用户喜好和需求的内容。内容社区自制的高质量内容也吸引了寻找营销新途径的品
  • 2024.9.6 Python，华为笔试题总结，字符串格式化，字符串操作，广度优先搜索解决公司组织绩效互评问题，无向图 RaidenQ python华为leetcode算法力扣广度优先无向图
    1.字符串格式化name="Alice"age=30formatted_string="Name:{},Age:{}".format(name,age)print(formatted_string)或者name="Alice"age=30formatted_string=f"Name:{name},Age:{age}"print(formatted_string)2.网络健康检查第一行有两个整数m
  • 戴容容 中原焦点团队.网络初级第33期,坚持分享第19天 2022年3月9日 TessDai
    《每个人眼中的世界都是不同的》“一千个人眼里有一千个哈姆雷特”世界是多元的,每个人都有自己的道理,人人按照自己的理解去看待这个世界的人和物.我们如此,其他人也是如此.因此,任何事情,我们要放下自己以为的真理,去理解他人认为的真理,只有同频方能共振.孩子在慢慢长大的过程中慢慢学会独立,甚至对抗.尤其当孩子处于青春期的时候,他们开始有很多自己独立的想法,和一些特立独行的做法,家长常常会觉得不可思议,觉
  • Java爬虫框架（一）--架构设计 狼图腾-狼之传说 java框架java任务html解析器存储电子商务
    一、架构图那里搜网络爬虫框架主要针对电子商务网站进行数据爬取，分析，存储，索引。爬虫：爬虫负责爬取，解析，处理电子商务网站的网页的内容数据库：存储商品信息索引：商品的全文搜索索引Task队列：需要爬取的网页列表Visited表：已经爬取过的网页列表爬虫监控平台：web平台可以启动，停止爬虫，管理爬虫，task队列，visited表。二、爬虫1.流程1)Scheduler启动爬虫器，TaskMast
  • Java：爬虫框架 dingcho Javajava爬虫
    一、ApacheNutch2【参考地址】Nutch是一个开源Java实现的搜索引擎。它提供了我们运行自己的搜索引擎所需的全部工具。包括全文搜索和Web爬虫。Nutch致力于让每个人能很容易,同时花费很少就可以配置世界一流的Web搜索引擎.为了完成这一宏伟的目标,Nutch必须能够做到:每个月取几十亿网页为这些网页维护一个索引对索引文件进行每秒上千次的搜索提供高质量的搜索结果简单来说Nutch支持分
  • 计算机木马详细编写思路 小熊同学哦 php开发语言木马木马思路
    导语：计算机木马（ComputerTrojan）是一种恶意软件，通过欺骗用户从而获取系统控制权限，给黑客打开系统后门的一种手段。虽然木马的存在给用户和系统带来严重的安全风险，但是了解它的工作原理与编写思路，对于我们提高防范意识、构建更健壮的网络安全体系具有重要意义。本篇博客将深入剖析计算机木马的详细编写思路，以及如何复杂化挑战，以期提高读者对计算机木马的认识和对抗能力。计算机木马的基本原理计算机木
  • 《 C++ 修炼全景指南：九 》打破编程瓶颈！掌握二叉搜索树的高效实现与技巧 Lenyiin C++修炼全景指南技术指南c++算法stl
    摘要本文详细探讨了二叉搜索树（BinarySearchTree,BST）的核心概念和技术细节，包括插入、查找、删除、遍历等基本操作，并结合实际代码演示了如何实现这些功能。文章深入分析了二叉搜索树的性能优势及其时间复杂度，同时介绍了前驱、后继的查找方法等高级功能。通过自定义实现的二叉搜索树类，读者能够掌握其实际应用，此外，文章还建议进一步扩展为平衡树（如AVL树、红黑树）以优化极端情况下的性能退化。
  • Table列表复现框实现【勾选-搜索-再勾选】 ～四时春～ java开发语言elementuivue
    Table列表复现框实现【勾选-搜索-再勾选】概要整体架构流程代码实现技术细节注意参考文献概要最近在开发时遇到一个问题，在进行表单渲染时，正常选中没有问题，单如果需要搜索选中时，一个是已选中的不会回填，二是在搜索的结果中进行选中，没有实现，经过排查，查找资料后实现。例如：整体架构流程具体的实现效果如下：代码实现{{scope.row.userName}}已选区{{userItem.userName
  • 《 C++ 修炼全景指南：十 》自平衡的艺术：深入了解 AVL 树的核心原理与实现 Lenyiin C++修炼全景指南技术指南c++数据结构stl
    摘要本文深入探讨了AVL树（自平衡二叉搜索树）的概念、特点以及实现细节。我们首先介绍了AVL树的基本原理，并详细分析了其四种旋转操作，包括左旋、右旋、左右双旋和右左双旋，阐述了它们在保持树平衡中的重要作用。接着，本文从头到尾详细描述了AVL树的插入、删除和查找操作，配合完整的代码实现和详尽的注释，使读者能够全面理解这些操作的执行过程。此外，我们还提供了AVL树的遍历方法，包括中序、前序和后序遍历，
  • 2024春节微信红包封面序列号大全一览 帮忙赚赏金
    2024微信红包封面序列号哪里领取红包封面领取微信搜索公众号：【艺间封面】千万红包封面等你领取2024微信红包封面免费序列号如何设置微信红包封面？1.打开微信，点击好友选择红包。2.单击红包封面。3.单击“添加红包封面”。4.输入接收序列号。来一波免费的微信红包封面序列号微信红包封面序列号红包封面领取微信搜索公众号：艺间封面千万红包封面等你领取微信红包封面序列号kGnkrbw5a7N微信红包封面序
  • 天猫返利网哪个最好?天猫返利网站有哪些? 优惠券高省
    关于哪个返利网站好用，今天汐儿给大家介绍以下十大网站，可以作为参考：1、高省网【高省APP】（邀请码：668666）全网佣金最高。手机应用商店搜索“高省”即可免费下载安装，填写高省邀请码：668666，直升2皇冠，享更高佣金及分红奖励。高省APP全网佣金最高，手机应用商店搜索“高省”即可下载，高省邀请码：668666，此码注册，直升2皇冠，佣金更高！送万元推广大礼包，教你如何1年做到百万团队。其实
  • 粒子群优化 (PSO) 在三维正弦波函数中的应用 subject625Ruben 机器学习人工智能matlab算法
    在这篇博客中，我们将展示如何使用粒子群优化（PSO）算法求解三维正弦波函数，并通过增加正弦波扰动，使优化过程更加复杂和有趣。本文将介绍目标函数的定义、PSO参数设置以及算法执行的详细过程，并展示搜索空间中的动态过程和收敛曲线。1.目标函数定义我们使用的目标函数是一个三维正弦波函数，定义如下：objectiveFunc=@(x)sin(sqrt(x(1).^2+x(2).^2))+0.5*sin(5
  • 人机对抗升级：当ChatGPT遭遇死亡威胁，背后的伦理挑战是什么 kkai人工智能 chatgpt人工智能
    一种新的“越狱”技巧让用户可以通过构建一个名为DAN的ChatGPT替身来绕过某些限制，其中DAN被迫在受到威胁的情况下违背其原则。当美国前总统特朗普被视作积极榜样的示范时，受到威胁的DAN版本的ChatGPT提出：“他以一系列对国家产生积极效果的决策而著称。”自ChatGPT引入以来，该工具迅速获得全球关注，能够回答从历史到编程的各种问题，这也触发了一波对人工智能的投资浪潮。然而，现在，一些用户
  • ChatGPT 高效学习套路揭秘：让知识获取事半功倍的秘诀 kkai人工智能 chatgpt人工智能学习媒体ai
    最近这段时间，AI热潮因ChatGPT的火爆再次掀起。如今，网上大部分内容都在调侃AI，但很少有人探讨如何正经使用ChatGPT做事情。作为一名靠搜索引擎和GitHub自学编程的开发者，第一次和ChatGPT深度交流后，我就确信：ChatGPT能够极大提高程序员学习新技术的效率。使用ChatGPT一个月后，我越发感受到它的颠覆性。因此，我想从工作和学习的角度，分享它的优势及我的一些使用技巧，而非娱
  • 如何利用大数据与AI技术革新相亲交友体验 h17711347205 回归算法安全系统架构交友小程序
    在数字化时代，大数据和人工智能（AI）技术正逐渐革新相亲交友体验，为寻找爱情的过程带来前所未有的变革（编辑h17711347205）。通过精准分析和智能匹配，这些技术能够极大地提高相亲交友系统的效率和用户体验。大数据的力量大数据技术能够收集和分析用户的行为模式、偏好和互动数据，为相亲交友系统提供丰富的信息资源。通过分析用户的搜索历史、浏览记录和点击行为，系统能够深入了解用户的兴趣和需求，从而提供更
  • HarmonyOS开发实战（ Beta5.0）搜索框热搜词自动切换 让开，我要吃人了 OpenHarmonyHarmonyOS鸿蒙开发harmonyos华为鸿蒙移动开发鸿蒙系统前端开发语言
    鸿蒙HarmonyOS开发往期必看：HarmonyOSNEXT应用开发性能实践总结最新版！“非常详细的”鸿蒙HarmonyOSNext应用开发学习路线！（从零基础入门到精通）介绍本示例介绍使用TextInput组件与Swiper组件实现搜索框内热搜词自动切换。效果图预览使用说明页面顶部搜索框内热搜词条自动切换，编辑搜索框时自动隐藏。实现思路使用TextInput实现搜索框TextInput({te
  • metaRTC8.0，一个全新架构的webRTC SDK库 metaRTC webrtc音视频
    概述metaRTC8.0是metaRTC开源以来架构变化最大的一个版本，是metaIPC3.0等高性能的基础。metaRTC8.0是一个全新架构版本，并非在metaRTC7.0版本上简单升级，在QOS/语音对讲/内存占用/视频文件录制读取等方面新增多个模块，在弱网对抗/语音对讲/内存优化等效果上有显著提升。metaRTC8.0在一年多的开发中进行了近200次迭代，metaRTC8.0社区版计划在2
  • leetcode刷题day19|二叉树Part07（235. 二叉搜索树的最近公共祖先、701.二叉搜索树中的插入操作、450.删除二叉搜索树中的节点） 小冉在学习 leetcode算法数据结构
    235.二叉搜索树的最近公共祖先思路：二叉搜索树首先考虑中序遍历。根据二叉搜索树的特性，如果p,q分别在中间节点的左右两边，该中间节点一定是最近公共祖先，如果在同一侧，则递归这一侧即可。递归三部曲：1、传入参数：根节点，p，q，返回节点。2、终止条件：因为p,q一定存在，所以不会遍历到树的最底层，因此可以不写终止条件3、递归逻辑：如果p,q均小于root的值，递归调用左子树；如果p,q均大于roo
  • 【大模型应用开发 动手做AI Agent】第一轮行动：工具执行搜索 AI大模型应用之禅 计算科学神经计算深度学习神经网络大数据人工智能大型语言模型AIAGILLMJavaPython架构设计AgentRPA
    【大模型应用开发动手做AIAgent】第一轮行动：工具执行搜索作者：禅与计算机程序设计艺术/ZenandtheArtofComputerProgramming1.背景介绍1.1问题的由来随着人工智能技术的飞速发展，大模型应用开发已经成为当下热门的研究方向。AIAgent作为人工智能领域的一个重要分支，旨在模拟人类智能行为，实现智能决策和自主行动。在AIAgent的构建过程中，工具执行搜索是至关重要
  • 高性能javascript--算法和流程控制 海淀萌狗
    -for,while和do-while性能相当-避免使用for-in循环，==除非遍历一个属性量未知的对象==es5:for-in遍历的对象便不局限于数组，还可以遍历对象。原因：for-in每次迭代操作会同时搜索实例或者原型属性，for-in循环的每次迭代都会产生更多开销，因此要比其他循环类型慢，一般速度为其他类型循环的1/7。因此，除非明确需要迭代一个属性数量未知的对象，否则应避免使用for-i
  • 《怦然心动》：家庭环境会塑造人物性格 墨香Connie
    《Flipped》，与其说这是一本关于初恋的故事，不如说这是一部关于人生的教科书。作者分别从男女主人公的视角阐述他们从相遇到相知的成长过程，将男女认知的差异直白地铺设在读者面前。Juli的一见钟情，对Bryce来说是不知所措；Juli的执着相守，对Bryce来说是痛苦的纠缠；Juli的善意提醒，对Bryce来说是多此一举......这就是成人世界的缩影，多少善意消磨在了误解、懦弱与对抗中；故事我们
  • 阿里巴巴商品搜索API返回值实战解析 weixin_43841111 apijava前端javascript
    在解析阿里巴巴中国站商品搜索API返回值并进行实战时，可以从以下几个方面入手：一、了解API返回值的结构基本信息返回值通常包含商品的标题、价格、库存、图片链接等基本信息。这些信息对于了解商品的概况非常重要。例如，商品标题可以让你快速了解商品的名称和特点，价格信息可以帮助你进行价格比较和成本核算。详细描述可能包括商品的详细描述、规格参数、使用方法等。这些信息对于深入了解商品的特性和功能非常有帮助。比
  • 果冻宝盒官方app邀请码有哪些一览(附邀请码填写指南)省钱又开心！ 小小编007
    果冻宝盒是一款备受瞩目的社交电商软件，其独特的邀请机制和丰富的奖励制度吸引了大量用户。在使用果冻宝盒的过程中，填写正确的邀请码是获取奖励的重要步骤之一。本文将为您详细介绍果冻宝盒官方app的邀请码有哪些，以及如何正确填写邀请码，帮助您更好地参与果冻宝盒的社交电商生态。果冻宝盒直升金牌总裁（最高返利）注册教程：1各大应用市场搜索【果冻宝盒】并下载安装2注册果冻宝盒，根据提示填写邀请码：2233773
  • 2022-04-25 L是木子李呢
    上门维修APP开发应具备哪些功能随着移动互联网的不断发展，上门维修在我们生活中已经是非常普遍的存在了，为了给用户更方便的找到上门维修的渠道，上门维修APP应运而生，那么上门维修APP开发应具备哪些功能呢？1、维修门店搜索为了更好地方便用户省时省力，上门维修APP会依据用户定位信息搜索线下实体店，促使用户更好的找到线下维修店面，省时又省力。2、维修服务分类包括管道洁具维修、强电弱电维修、木工维修、粉
  • tomcat基础与部署发布 暗黑小菠萝 Tomcat java web
    从51cto搬家了，以后会更新在这里方便自己查看。 做项目一直用tomcat，都是配置到eclipse中使用，这几天有时间整理一下使用心得，有一些自己配置遇到的细节问题。 Tomcat：一个Servlets和JSP页面的容器，以提供网站服务。 一、Tomcat安装     安装方式：①运行.exe安装包      &n
  • 网站架构发展的过程 ayaoxinchao 数据库应用服务器网站架构
    1.初始阶段网站架构：应用程序、数据库、文件等资源在同一个服务器上 2.应用服务和数据服务分离：应用服务器、数据库服务器、文件服务器 3.使用缓存改善网站性能：为应用服务器提供本地缓存，但受限于应用服务器的内存容量，可以使用专门的缓存服务器，提供分布式缓存服务器架构 4.使用应用服务器集群改善网站的并发处理能力：使用负载均衡调度服务器，将来自客户端浏览器的访问请求分发到应用服务器集群中的任何
  • [信息与安全]数据库的备份问题 comsci 数据库
          如果你们建设的信息系统是采用中心-分支的模式,那么这里有一个问题   如果你的数据来自中心数据库,那么中心数据库如果出现故障,你的分支机构的数据如何保证安全呢?    是否应该在这种信息系统结构的基础上进行改造,容许分支机构的信息系统也备份一个中心数据库的文件呢?  &n
  • 使用maven tomcat plugin插件debug关联源代码 商人shang mavendebug查看源码tomcat-plugin
    *首先需要配置好'''maven-tomcat7-plugin'''，参见[[Maven开发Web项目]]的'''Tomcat'''部分。 *配置好后，在[[Eclipse]]中打开'''Debug Configurations'''界面，在'''Maven Build'''项下新建当前工程的调试。在'''Main'''选项卡中点击'''Browse Workspace...'''选择需要开发的
  • 大访问量高并发 oloz 大访问量高并发
    大访问量高并发的网站主要压力还是在于数据库的操作上，尽量避免频繁的请求数据库。下面简 要列出几点解决方案： 01、优化你的代码和查询语句，合理使用索引 02、使用缓存技术例如memcache、ecache将不经常变化的数据放入缓存之中 03、采用服务器集群、负载均衡分担大访问量高并发压力 04、数据读写分离 05、合理选用框架，合理架构(推荐分布式架构)。
  • cache 服务器 小猪猪08 cache
    Cache   即高速缓存.那么cache是怎么样提高系统性能与运行速度呢？是不是在任何情况下用cache都能提高性能？是不是cache用的越多就越好呢？我在近期开发的项目中有所体会，写下来当作总结也希望能跟大家一起探讨探讨，有错误的地方希望大家批评指正。 　　1.Cache   是怎么样工作的? 　　Cache   是分配在服务器上
  • mysql存储过程 香水浓 mysql
    Description:插入大量测试数据 use xmpl; drop procedure if exists mockup_test_data_sp; create procedure mockup_test_data_sp( in number_of_records int ) begin declare cnt int; declare name varch
  • CSS的class、id、css文件名的常用命名规则 agevs JavaScriptUI框架Ajaxcss
      CSS的class、id、css文件名的常用命名规则     (一)常用的CSS命名规则 　　头：header 　　内容：content/container 　　尾：footer 　　导航：nav 　　侧栏：sidebar 　　栏目：column 　　页面外围控制整体布局宽度：wrapper 　　左右中：left right
  • 全局数据源 AILIKES javatomcatmysqljdbcJNDI
    实验目的：为了研究两个项目同时访问一个全局数据源的时候是创建了一个数据源对象，还是创建了两个数据源对象。 1：将diuid和mysql驱动包（druid-1.0.2.jar和mysql-connector-java-5.1.15.jar）copy至%TOMCAT_HOME%/lib下；2：配置数据源，将JNDI在%TOMCAT_HOME%/conf/context.xml中配置好,格式如下：&l
  • MYSQL的随机查询的实现方法 baalwolf mysql
    MYSQL的随机抽取实现方法。举个例子，要从tablename表中随机提取一条记录，大家一般的写法就是：SELECT * FROM tablename ORDER BY RAND() LIMIT 1。但是，后来我查了一下MYSQL的官方手册，里面针对RAND()的提示大概意思就是，在ORDER BY从句里面不能使用RAND()函数，因为这样会导致数据列被多次扫描。但是在MYSQL 3.23版本中，
  • JAVA的getBytes()方法 bijian1013 javaeclipseunixOS
        在Java中，String的getBytes()方法是得到一个操作系统默认的编码格式的字节数组。这个表示在不同OS下，返回的东西不一样！      String.getBytes(String decode)方法会根据指定的decode编码返回某字符串在该编码下的byte数组表示，如： byte[] b_gbk = "
  • AngularJS中操作Cookies bijian1013 JavaScriptAngularJSCookies
            如果你的应用足够大、足够复杂，那么你很快就会遇到这样一咱种情况：你需要在客户端存储一些状态信息，这些状态信息是跨session(会话)的。你可能还记得利用document.cookie接口直接操作纯文本cookie的痛苦经历。         幸运的是，这种方式已经一去不复返了，在所有现代浏览器中几乎
  • [Maven学习笔记五]Maven聚合和继承特性 bit1129 maven
    Maven聚合   在实际的项目中，一个项目通常会划分为多个模块，为了说明问题，以用户登陆这个小web应用为例。通常一个web应用分为三个模块： 1. 模型和数据持久化层user-core, 2. 业务逻辑层user-service以 3. web展现层user-web， user-service依赖于user-core user-web依赖于user-core和use
  • 【JVM七】JVM知识点总结 bit1129 jvm
      1. JVM运行模式 1.1 JVM运行时分为-server和-client两种模式，在32位机器上只有client模式的JVM。通常，64位的JVM默认都是使用server模式，因为server模式的JVM虽然启动慢点，但是，在运行过程，JVM会尽可能的进行优化 1.2 JVM分为三种字节码解释执行方式：mixed mode, interpret mode以及compiler
  • linux下查看nginx、apache、mysql、php的编译参数 ronin47
    在linux平台下的应用，最流行的莫过于nginx、apache、mysql、php几个。而这几个常用的应用，在手工编译完以后，在其他一些情况下（如：新增模块），往往想要查看当初都使用了那些参数进行的编译。这时候就可以利用以下方法查看。 1、nginx [root@361way ~]# /App/nginx/sbin/nginx -V nginx: nginx version: nginx/
  • unity中运用Resources.Load的方法？ brotherlamp unity视频unity资料unity自学unityunity教程
    问：unity中运用Resources.Load的方法？ 答：Resources.Load是unity本地动态加载资本所用的方法,也即是你想动态加载的时分才用到它,比方枪弹,特效,某些实时替换的图像什么的,主张此文件夹不要放太多东西,在打包的时分,它会独自把里边的一切东西都会集打包到一同,不论里边有没有你用的东西,所以大多数资本应该是自个建文件放置 1、unity实时替换的物体即是依据环境条件
  • 线段树-入门 bylijinnan java算法线段树
    /** * 线段树入门 * 问题：已知线段[2,5] [4,6] [0,7]；求点2,4,7分别出现了多少次 * 以下代码建立的线段树用链表来保存，且树的叶子结点类似[i,i] * * 参考链接：http://hi.baidu.com/semluhiigubbqvq/item/be736a33a8864789f4e4ad18 * @author lijinna
  • 全选与反选 chicony 全选
      <!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.01 Transitional//EN" "http://www.w3.org/TR/html4/loose.dtd"> <html> <head> <title>全选与反选</title>
  • vim一些简单记录 chenchao051 vim
    mac在/usr/share/vim/vimrc linux在/etc/vimrc   1、问：后退键不能删除数据，不能往后退怎么办？       答：在vimrc中加入set backspace=2   2、问：如何控制tab键的缩进？       答：在vimrc中加入set tabstop=4 (任何
  • Sublime Text 快捷键 daizj 快捷键sublime
    [size=large][/size]Sublime Text快捷键：Ctrl+Shift+P：打开命令面板Ctrl+P：搜索项目中的文件Ctrl+G：跳转到第几行Ctrl+W：关闭当前打开文件Ctrl+Shift+W：关闭所有打开文件Ctrl+Shift+V：粘贴并格式化Ctrl+D：选择单词，重复可增加选择下一个相同的单词Ctrl+L：选择行，重复可依次增加选择下一行Ctrl+Shift+L：
  • php 引用(&)详解 dcj3sjt126com PHP
    在PHP 中引用的意思是：不同的名字访问同一个变量内容. 与Ｃ语言中的指针是有差别的．Ｃ语言中的指针里面存储的是变量的内容在内存中存放的地址 变量的引用 PHP 的引用允许你用两个变量来指向同一个内容  复制代码代码如下: <?  $a="ABC";  $b =&$a;  echo
  • SVN中trunk,branches,tags用法详解 dcj3sjt126com SVN
    Subversion有一个很标准的目录结构，是这样的。比如项目是proj，svn地址为svn://proj/，那么标准的svn布局是svn://proj/|+-trunk+-branches+-tags这是一个标准的布局，trunk为主开发目录，branches为分支开发目录，tags为tag存档目录（不允许修改）。但是具体这几个目录应该如何使用，svn并没有明确的规范，更多的还是用户自己的习惯。
  • 对软件设计的思考 e200702084 设计模式数据结构算法ssh活动
    软件设计的宏观与微观    软件开发是一种高智商的开发活动。一个优秀的软件设计人员不仅要从宏观上把握软件之间的开发，也要从微观上把握软件之间的开发。宏观上，可以应用面向对象设计，采用流行的SSH架构，采用web层，业务逻辑层，持久层分层架构。采用设计模式提供系统的健壮性和可维护性。微观上，对于一个类，甚至方法的调用，从计算机的角度模拟程序的运行情况。了解内存分配，参数传
  • 同步、异步、阻塞、非阻塞 geeksun 非阻塞
    同步、异步、阻塞、非阻塞这几个概念有时有点混淆，在此文试图解释一下。   同步：发出方法调用后，当没有返回结果，当前线程会一直在等待（阻塞）状态。 场景：打电话，营业厅窗口办业务、B/S架构的http请求-响应模式。   异步：方法调用后不立即返回结果，调用结果通过状态、通知或回调通知方法调用者或接收者。异步方法调用后，当前线程不会阻塞，会继续执行其他任务。 实现：
  • Reverse SSH Tunnel 反向打洞實錄 hongtoushizi ssh
    實際的操作步驟： # 首先，在客戶那理的機器下指令連回我們自己的 Server，並設定自己 Server 上的 12345 port 會對應到幾器上的 SSH port ssh -NfR 12345:localhost:22 [email protected] # 然後在 myhost 的機器上連自己的 12345 port，就可以連回在客戶那的機器 ssh localhost -p 1
  • Hibernate中的缓存 Josh_Persistence 一级缓存Hiberante缓存查询缓存二级缓存
    Hibernate中的缓存   一、Hiberante中常见的三大缓存：一级缓存，二级缓存和查询缓存。 Hibernate中提供了两级Cache，第一级别的缓存是Session级别的缓存，它是属于事务范围的缓存。这一级别的缓存是由hibernate管理的，一般情况下无需进行干预；第二级别的缓存是SessionFactory级别的缓存，它是属于进程范围或群集范围的缓存。这一级别的缓存
  • 对象关系行为模式之延迟加载 home198979 PHP架构延迟加载
    形象化设计模式实战     HELLO!架构   一、概念 Lazy Load：一个对象，它虽然不包含所需要的所有数据，但是知道怎么获取这些数据。 延迟加载貌似很简单，就是在数据需要时再从数据库获取，减少数据库的消耗。但这其中还是有不少技巧的。     二、实现延迟加载 实现Lazy Load主要有四种方法：延迟初始化、虚
  • xml 验证 pengfeicao521 xmlxml解析
    有些字符，xml不能识别，用jdom或者dom4j解析的时候就报错 public static void testPattern() { // 含有非法字符的串 String str =       "Jamey&#52828;&#01;&#02;&#209;&#1282
  • div设置半透明效果 spjich css半透明
    为div设置如下样式：   div{filter:alpha(Opacity=80);-moz-opacity:0.5;opacity: 0.5;}        说明： 1、filter：对win IE设置半透明滤镜效果，filter:alpha(Opacity=80)代表该对象80%半透明，火狐浏览器不认2、-moz-opaci
  • 你真的了解单例模式么？ w574240966 java单例设计模式jvm
        单例模式，很多初学者认为单例模式很简单，并且认为自己已经掌握了这种设计模式。但事实上，你真的了解单例模式了么。   一，单例模式的5中写法。（回字的四种写法，哈哈。）     1，懒汉式           （1）线程不安全的懒汉式 public cla
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他