数据结构---平衡二叉树(AVL)
>AVL树 取自 G.M.Adelson-Velsky 和E.M.Landis
1962年的论文首次提出
满二叉树:除了叶子节点其他酒店都有左孩子和右孩子。

完全二叉树:所有叶子节点最多相差一层。
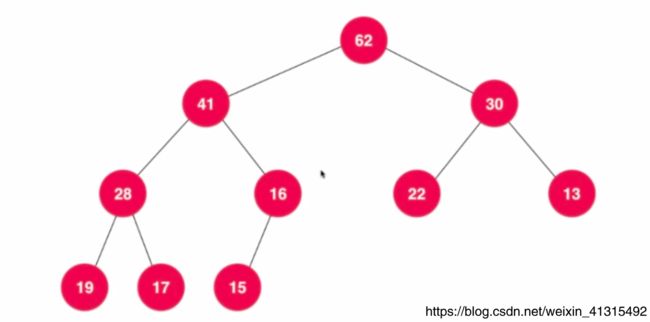
定义:对于任意一个节点,左子树和柚子树的高度差不能超过1
如上图12 节点 的左子树 8、 5、 4高度为3
12 的左子树 18和 17 高度为2 相差不超过1
8的左子树 5 和 4 高度为 2 ,8 的右子树11 高度为1 相差不超过1
18 的左子树 17 高度为1 18的右子树 高度为 0 相差不超过1
平衡二叉树的高度和节点数量之间的关系也是O(logn)的
平衡二叉树是在二分搜索树上进行拓展
//计算节点的高度
private int getNodeHeight(Node node){
if(node == null)
return 0;
return node.height;
}
//向二分搜索树添加
private Node add(Node node,K key,V value){
if(node==null){
size ++;
return new Node(key,value);
}
if(key.compareTo(node.key) > 0)
node.right = add(node.right,key,value);
else if(key.compareTo(node.key)<0)
node.left = add(node.left,key,value);
else
node.value = value;
//每次 插入好 就是上面的逻辑 会把节点插入适合的位置 找到了位置后 计算自己的高度
node.height = 1 + Math.max(getNodeHeight(node.left),getNodeHeight(node.right));
//计算平衡因子 找到当前节点的左孩子和右孩子 的 高度相减计算平衡影子
int balanceFactor = getBalanceFactor(node);
//如果平衡影子直接高度相差的绝对值大于1
if(Math.abs(balanceFactor)>1)
//就认为这不是平衡的
System.out.println("unbalanced" + balanceFactor);
//最后返回这个节点
return node;
}
//计算平衡因子
private int getBalanceFactor(Node node){
if(node == null)
return 0;
return getNodeHeight(node.left)-getNodeHeight(node.right);
}
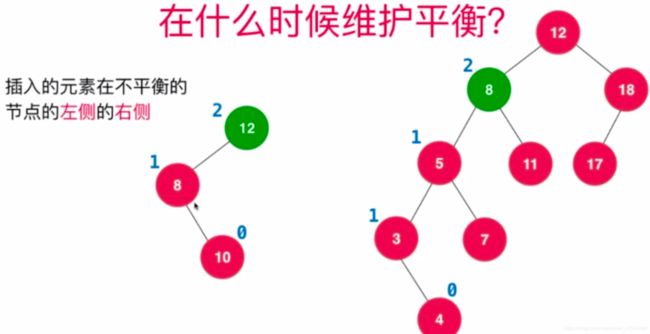
 如上图插入 8 < 12 往左边插入 此时12高度为2 平衡影子为1 5<8 往左边插入 此时12 的 高度为3 平衡影子为2 此时已经是不平衡的树了。
如上图插入 8 < 12 往左边插入 此时12高度为2 平衡影子为1 5<8 往左边插入 此时12 的 高度为3 平衡影子为2 此时已经是不平衡的树了。
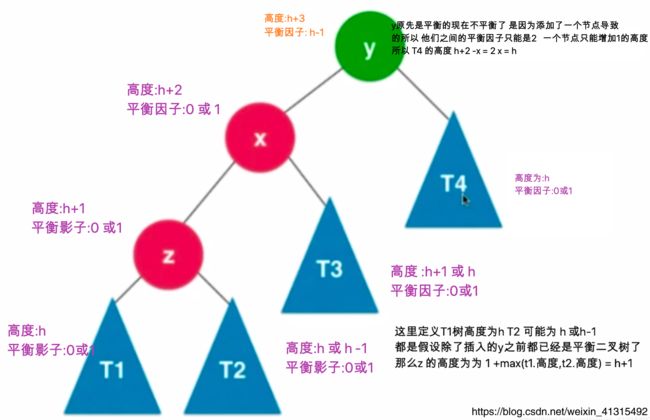
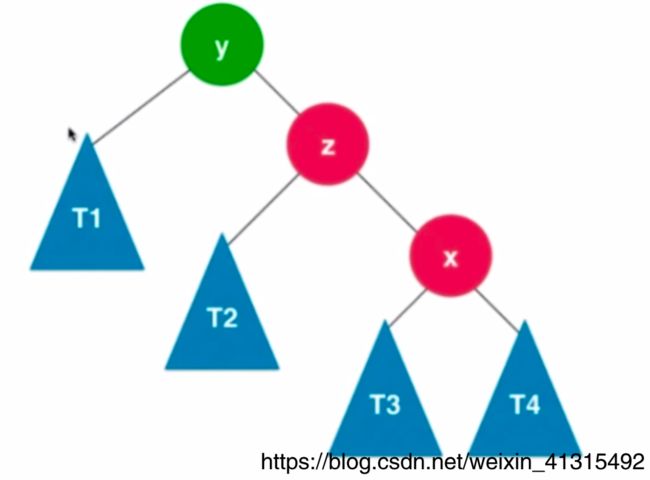
如上图的关系可以得出: T 1 < z < T 2 < x < T 3 < y < T 4 T_1
由于 y y y的平衡影子为2 不满足 平衡二叉树 所以找到 y y y高度较高的方向 y y y的左子树 由于 x < y x
右旋转(RR)
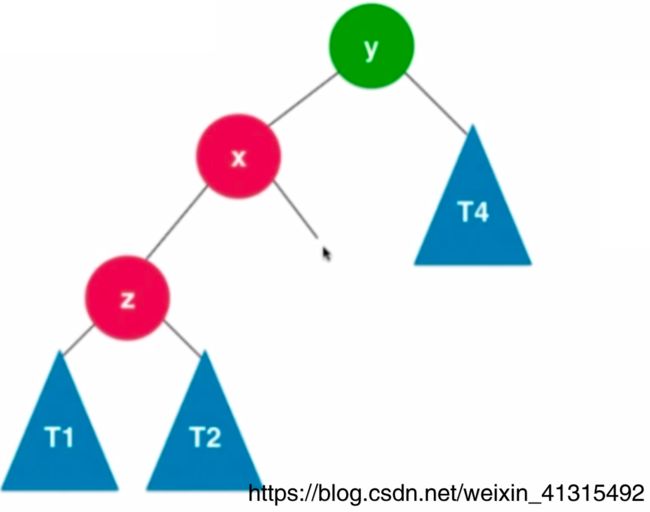
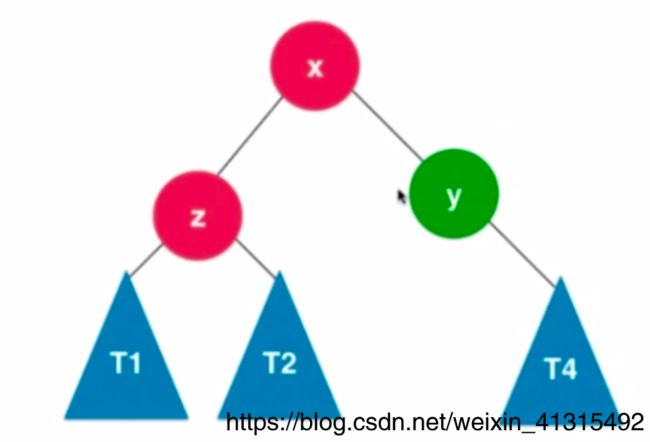
使x.右子树 = y
同时根据公式可知 T 3 < y < T 4 T_3
y.left =t3
上图是一个右旋转的过程 旋转后依然满足二叉树的性质 并且也颗平衡二叉树。
下面上代码
/**
* 对节点y进行右旋操作,返回旋转后新的根节点x
*
* // y x
* // / \ / \
* // x T4 右旋(y) z y
* // / \ ========> / \ / \
* // z T3 T1 T2 T3 T4
* // / \
* // T1 T2
* @param y 传入的是要更新的平衡因子不对的node 也就是↑y
* @return
*/
private Node rightRotate(Node y){
//取出x节点从y的left节点
Node x = y.left;
//交换node零食存储t3
Node T3 =x.left;
//x的右子树等于y
x.right = y;
//y的左子树等于t3
y.left = T3;
//由于x,和 y发生了旋转高度需要改变 获取左孩子和右孩子节点高度 重新计算
y.height = 1 + Math.max(getNodeHeight(y.left),getNodeHeight(y.right));
x.height = 1 + Math.max(getNodeHeight(y.left),getNodeHeight(y.right));
//返回 x 和 y 进行旋转后的 node x
return x;
}
左旋转(LL)
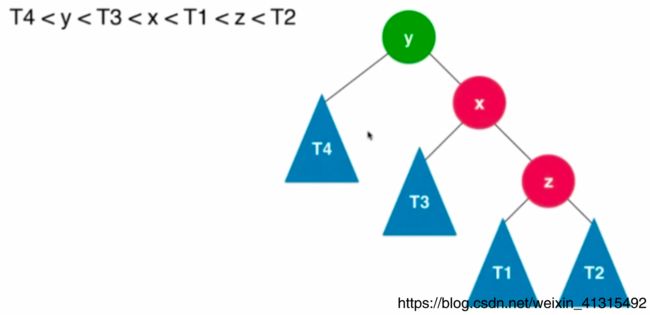
最旋转和 右旋转是一样的过程
由二叉树性质可得 T 4 < y < T 3 < x < T 1 < z < T 2 T4
跟旋转右子树一样的性质一样
先将取出 x节点
取出t3节点
T 4 < y < T 3 < x T4
既然y比T3小 那为什么不放在t3的左子树下面呢 如果这么做 就变成2h+1 当t3取 h+1 时 t3+ y + t4 = h+1 +1 + h = 2h+2 此时T4 没有了 t3 只有1的高度 只有h取到0时才能满足平衡二叉树的性质。
/**
* 对节点y进行右旋操作,返回旋转后新的根节点x
*
* // y x
* // / \ / \
* // T4 x 左旋(y) z y
* // / \ ======> / \ / \
* // T3 z T1 T2 T3 T4
* // / \
* // T1 T2
* @param y 传入的是要更新的平衡因子不对的node 也就是↑y
* @return
*/
private Node leftRotate(Node y){
//取出元素x
Node x = y.right;
Node T3 = x.left;
x.left= y;
y.right = T3;
//由于x,和 y发生了旋转高度需要改变 获取左孩子和右孩子节点高度 重新计算
y.height = 1 + Math.max(getNodeHeight(y.left),getNodeHeight(y.right));
x.height = 1 + Math.max(getNodeHeight(x.left),getNodeHeight(x.right));
return x;
}
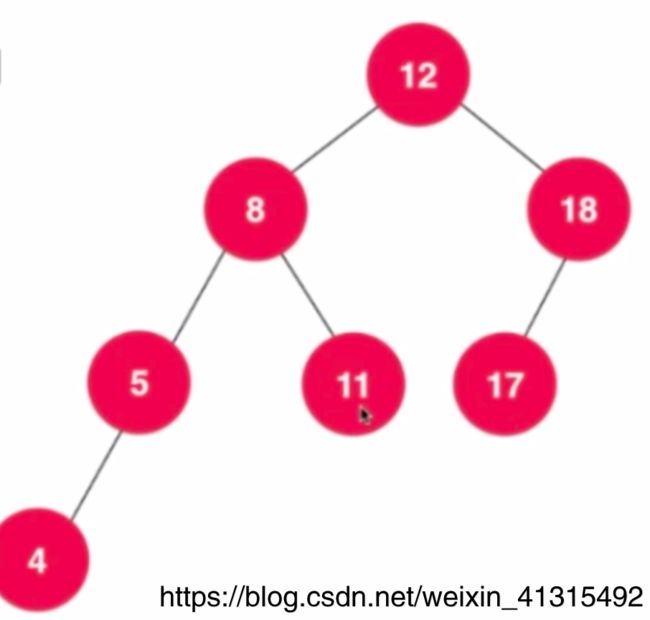
如果插入的元素在 左边的 右边如上图 是没法左旋转的 因为 10 和 12 都比8大。
左右旋转(LR)

对于在 y左节点的右节点 插入元素 我们先要将 x进行坐旋转
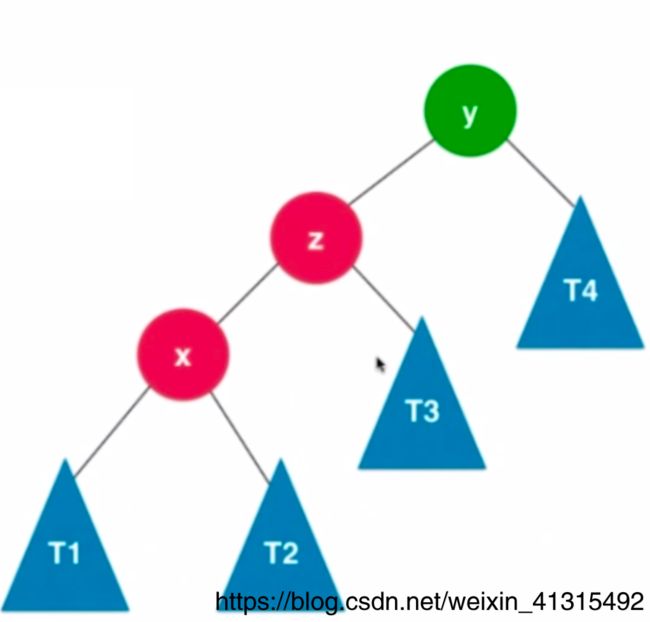
那么问题就转化为了 上面右旋转的问题了, 对y进行右旋转。
右左旋转(RL)
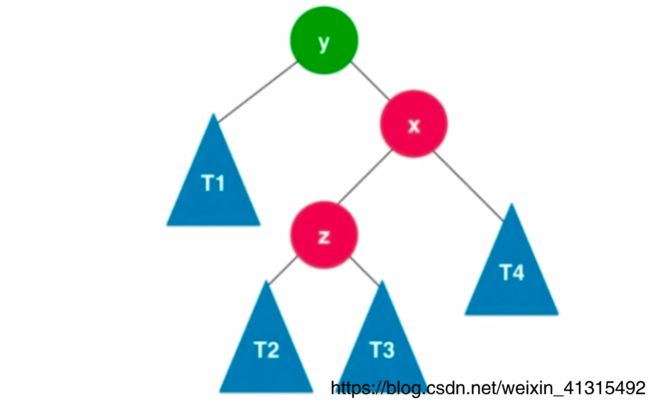
//LR
if(balanceFactor>1 && getBalanceFactor(node.left)< 0 ){
node.left = leftRotate(node.left);
return rightRotate(node);
}
//RL
if(balanceFactor<-1 && getBalanceFactor(node.right)> 0 ){
node.right = rightRotate(node.right);
return leftRotate(node);
}
以下是 平衡二叉树和二分查找树 做对比
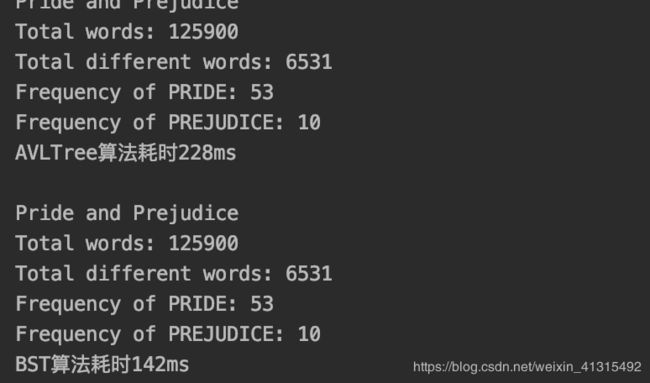
在加载傲慢与偏见这本书 的情况下 似乎 二叉树 会更好一些 这说明 本书单词排序比较随机 没有形成一颗严重失衡 的 二叉树 同时平衡二叉树 需要有不断地左旋 右旋 的去调整树的状态 这方面比二叉树更耗时 。
那让我们再来模拟最坏的情况 把这本书 所有单词 从大到小排序
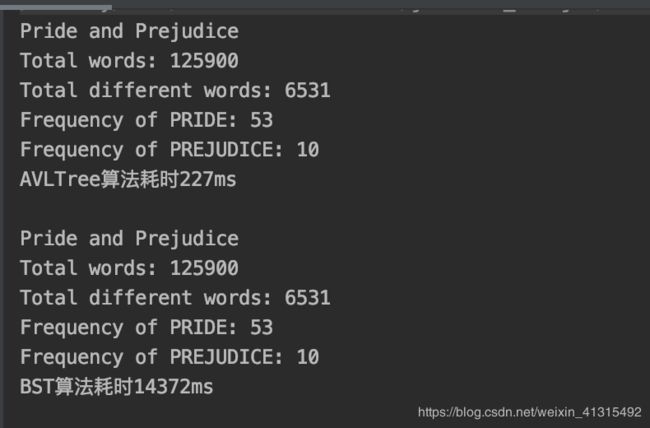
此时 这二叉树就退化成了只有 右孩子的 链表了 此时查询一个单词 就要遍历所有的单词了。
AVLtree github下载