TensorFlow学习笔记(二)——最简单的前后传播算法
前言:
不同的神经网络结构前向传播的方式也不一样, 本章将介绍最简单的全连接网络结构的前向传播算法,并且将展示如何通过TensorFlow实现这个算法。
一、前后传播算法简介
为了介绍神经网络的前向传播算法,需要先了解神经元的结构。 神经元是构成一个神经网络的最小单元,下图显示了一个最简单的神经元结构。
从图中可以看出,一个神经元有多个输入和一个输出。每个神经元的输入既可以是其他神经元的输出,也可以是整个神经网络的输入。所谓神经网络的结构就是指的不同神经元之间的连接结构。如图所示,一个最简单的神经元结构的输出就是所有输入的加权和,而不同输入的权重就是神经元的参数,神经网络的优化过程就是优化神经元中参数取值的过程。本章将重点介绍神经网络的前向传播过程。下图给出了一个简单的判断零件是否合格的三层全连接神经网络,之所以称之为全连接神经网络是因为相邻两层之间任意两个节点之间都有连接。下图中除了输入层之外的所有节点都代表了一个神经元的结构 。本小节将通过这个样例来解释前向传播的整个过程 。
计算神经网络的前向传播结果需要三部分信息:
第一个部分是神经网络的输入,这个输入就是从实体中提取的特征向量。比如在上图中有两个输入, 一个是零件的长度 ![]() ,一个是零件的质量
,一个是零件的质量![]() 。
。
第二个部分为神经网络的连接结构。神经网络是由神经元构成的,神经网络的结构给出不同神经元之间输入输出的连接关系。神经网络中的神经元也可以称之为节点,通常我们使用节点来指代神经网络中的神经元。 在上图中,![]() 节点有两个输入,他们分别是
节点有两个输入,他们分别是![]() 和
和![]() 的输出。而
的输出。而![]() 的输出则是节点 y的输入。
的输出则是节点 y的输入。
最后一个部分是每个神经元中的参数。在上图中用![]() 来表示神经元中的参数。
来表示神经元中的参数。![]() 的上标表明了神经网络的层数,比如
的上标表明了神经网络的层数,比如![]() 表示第一层节点的参数,而
表示第一层节点的参数,而![]() 表示第二层节点的参数。
表示第二层节点的参数。![]() 的下标表明了连接节点编号, 比如
的下标表明了连接节点编号, 比如 ![]() 表示连接
表示连接![]() 和
和![]() 节点的边上的权重。如何优化每一 条边的权重将是算法的关键,这一节假设这些权重是已知的。给定神经网络的输入,神经网络的结构以及边上权重,就可以通过前向传播算法来计算出神经网络的输出。下图展示了这个神经网络前向传播的过程:
节点的边上的权重。如何优化每一 条边的权重将是算法的关键,这一节假设这些权重是已知的。给定神经网络的输入,神经网络的结构以及边上权重,就可以通过前向传播算法来计算出神经网络的输出。下图展示了这个神经网络前向传播的过程:
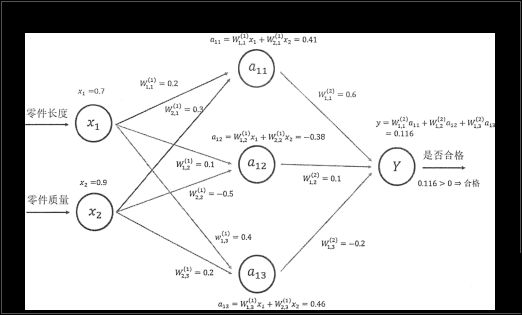
上图给出了输入层的取值![]() =0.7和
=0.7和![]() =0.9。从输入层开始一层一层地使用向前传播算法。首先隐藏层中有3个节点,每一个节点的取值都是输入层取值的加权和。下面给出了
=0.9。从输入层开始一层一层地使用向前传播算法。首先隐藏层中有3个节点,每一个节点的取值都是输入层取值的加权和。下面给出了![]() 节点取值的详细计算过程:
节点取值的详细计算过程:
![]()
![]() 和
和![]() 也可以通过类似的方法计算得到,上图中也给出了具体的计算公式。在得到第一层节点的取值之后, 可以进一步推导得到输出层的取值。类似的,输出层中节点的取值就是第一层的加权和:
也可以通过类似的方法计算得到,上图中也给出了具体的计算公式。在得到第一层节点的取值之后, 可以进一步推导得到输出层的取值。类似的,输出层中节点的取值就是第一层的加权和:
因为这个输出值大于阈值0,所以在这个样例中最后给出的答案又是:这个产品是合格的。这就是整个前向传播的算法。前向传播算法可以表示为矩阵乘法。将输入![]() 组织成一个1x2的矩阵
组织成一个1x2的矩阵 ![]() ,而
,而 ![]() 组织成一个2x3的矩阵:
组织成一个2x3的矩阵:
这样就将前向传播算法通过矩阵乘法的方式表达出来了。在TensorFlow中矩阵乘法是非常容易实现的。以下TensorFlow程序实现了上图所示神经网络的前向传播过程:
a=tf.matmu1(x, w1)
y=tf.matmu1(a, w2) 其中 tf.matmul实现了矩阵乘法的功能。到此为止已经详细地介绍了神经网络的前向传播算法,并且给出了TensorFlow程序来实现这个过程。这里面没有涉及到偏置(bias)、激活函数(activationfunction)等更加复杂的神经元结构,也没有卷积神经网络,LSTM结构等更加复杂的神经网络结构。对于这些更加复杂的神经网络,TensorFlow也提供了很好的支持,我们在以后再学习。
二、神经网络参数与 TensorFlow 变量
2.1 变量
在TensorFlow中,变量 ( tf.Variable) 的作用就是保存和更新神经网络中的参数 。和其他编程语言类似,TensorFlow中的变量也需要指定初始值。因为在神经网络中, 给参数赋予随机初始值最为常见,所以一般也使用随机数给TensorFlow中的变量初始化。下面一段代码给出了一种在TensorFlow中声明一个2x3的矩阵变量的方法:
#coding=gbk
import numpy
import tensorflow as tf
# 声明变量,调用TensorF1ow变量的声明函数tf.Variable
weights = tf.Variable(tf.random_normal([2, 3], stddev=2))
##我们打印变量weights的信息
with tf.Session() as sess:
sess.run(weights.initializer)
print(sess.run(weights))
print(weights)
print(sess.run(weights).dtype)
print(type(sess.run(weights)))
这段代码调用了 TensorFlow变量的声明函数tf.Variable。
在变量声明函数中给出了初始化这个变量的方法 。 TensorFlow 中变量的初始值可以设置成随机数、常数或者是通过其他变量的初始值计算得到。在上面的样例中,tfrandom_norma1([2, 3], stddev=2)会产生一个2x3的矩阵,矩阵中的元素是均值为0,标准差为2的随机数。tf.random norma1函数可以通过参数 mean来指定平均值,在没有指定时默认为 0。通过满足正太分布的随机数来初始化神经网络中的参数是一个非常常用的方法 。
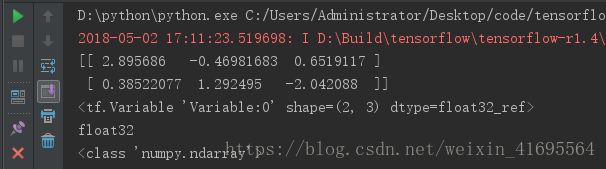
运行程序,结果为:
TensorFlow也支持通过常数来初始化一个变量。下表给出了 TensorFlow中常用的常量声明方法。
在神经网络中,偏置项(bias)通常会使用常数来设置初始值。以下代码给出了一个样例:
#coding=gbk
import numpy
import tensorflow as tf
# 声明变量,调用TensorF1ow变量的声明函数tf.Variable
biases = tf.Variable(tf.zeros([3]))
##我们打印变量biases的信息
with tf.Session() as sess:
sess.run(biases.initializer)
print(sess.run(biases))
print(biases)
print(sess.run(biases).dtype)
print(type(sess.run(biases)))
# 运行程序,输出以下结果:
# [0. 0. 0.]
#
# float32
# 这段代码生成一个初始值全部为0且长度为3的变量。除了使用随机数或者常数,TensorFlow也支持通过其他变量的初始值来初始化新的变量。以下代码给出了具体的方法:
#coding=gbk
import numpy
import tensorflow as tf
# 声明变量,调用TensorF1ow变量的声明函数tf.Variable
biases = tf.Variable(tf.ones([3]))
w1 = tf.Variable(biases.initialized_value())
w2 = tf.Variable(biases.initialized_value() * 2.0)
##我们打印变量的信息
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
print(sess.run(biases))
print(sess.run(w1))
print(sess.run(w2))
##运行程序,输出结果:
# [1. 1. 1.]
# [1. 1. 1.]
# [2. 2. 2.]以上代码中, w1的初始值被设置成了与biases变量相同。 w2的初始值则是biases初始值的两倍。在TensorFlow中,一个变量的值在被使用之前,这个变量的初始化过程需要被明确地调用。以下样例介绍了如何通过变量实现神经网络的参数并实现前向传播的过程:
#coding=gbk
import tensorflow as tf
#声明 w1、 w2两个变量。这里还通过seed参数设定了随机种子,这样可以保证每次运行得到的结果是一样的。
w1 = tf.Variable(tf.random_normal([2,3],stddev=1,seed=1))
w2 = tf.Variable(tf.random_normal([3,1],stddev=1,seed=1))
#暂时将输入的特征向量定义为一个常量。注意这里x是一个1*2的矩阵。
x= tf.constant([[0.7, 0.91]])
#通过前向传播算法获得神经网络的输出
a = tf.matmul(x,w1)
y= tf.matmul(a,w2)
#这里不能直接通过sess.run(y)来获取y的取值
# #因为w1和w2都还没有运行初始化过程,下面初始化了所有变量
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
print(sess.run(y))
##运行程序,输出结果:
# [[3.979256]]
上面这段程序实现了神经网络的前向传播过程。从这段代码可以看到,当声明了变量w1、 w2之后,可以通过w1和w2来定义神经网络的前向传播过程并得到中间结果a和最后答案y。定义 w1、 w2、 a和 y的过程对应了3.1.2小节中介绍的TensorFlow程序的第一 步。这一步定义了TensorFlow计算图中所有的计算,但这些被定义的计算在这一步中并不真正的运行。当需要运行这些计算并得到具体数字时,需要进入TensorFlow程序的第二步。
在 TensorF1ow程序的第二步会声明一个会话(session),并通过会话计算结果。在上面的样例中,当会话定义完成之后就可以开始真正运行定义好的计算了。但在计算 y之前, 需要将所有用到的变量初始化。也就是说,虽然在变量定义时给出了变量初始化的方法,但这个方法并没有被真正运行。所以在计算y之前,需要通过运行tf.global_variables_initializes()来给变量赋值。
2.2 placeholder机制
TensorFlow还提供了填充机制,可以在构建计算图时使用tf.placeholder()临时替代任意操作的张量,在调用Session对象的run()方法去执行计算图时,使用填充数据作为调用的参数,调用结束后,填充数据就消失。
placeholder相当于定义了一个位置,这个位置中的数据在程序运行时再指定。这样在程序中就不需要生成大量常量来提供输入数据,而只需要将数据通过 placeholder传入TensorFlow计算图。在 placeholder定义时,这个位置上的数据类型是需要指定的。 和其他张量一样,placeholder的类型也是不可以改变的。placeholder中数据的维度信息可以根据提供的数据推导得出,所以不一定要给出。下面给出了通过 placeholder实现运算的代码:
#coding=gbk
import tensorflow as tf
import numpy
w1 = tf.Variable(tf.random_normal([2,3],stddev=1,seed=1))
w2 = tf.Variable(tf.random_normal([3,1],stddev=1,seed=1))
#定义placeholder作为存放输入数据的地方。这里维度也不一定要定义
# 但如果维度是确定的, 那么给出维度可以降低出错的概率
x = tf.placeholder(tf.float32,shape=(1,2),name="input")
a= tf.matmul(x,w1)
y= tf.matmul(a,w2)
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
print(sess.run(y,feed_dict={x:numpy.mat([0.7,0.9])}))
##运行程序,输出结果:
# [[3.957578]]
三、通过 TensorFlow 训练神经网络模型
使用神经网络解决实际的分类或者回归问题时 (比如判断一个零件是否合格) 需要更好地设置参数取值。本节将简单介绍使用监督学习的方式来更合理地设置参数取值,同时也将给出 TensorFlow程序来完成这个过程。设置神经网络参数的过程就是神经网络的训练过程。只有经过有效训练的神经网络模型才可以真正的解决分类或者回归问题。
使用监督学习的方式设置神经网络参数需要有一个标注好的训练数据集。以判断零件是否合格为例,这个标注好的训练数据集就是收集的一批合格零件和一批不合格零件。监督学习最重要的思想就是,在已知答案的标注数据集上,模型给出的预测结果要尽量接近真实的答案。通过调整神经网络中的参数对训练数据进行拟合,可以使得模型对未知的样本提供预测的能力。
在神经网络优化算法中,最常用的方法是反向传播算法 (backpropagation)。反向传播算法的具体工作原理将在下面介绍。
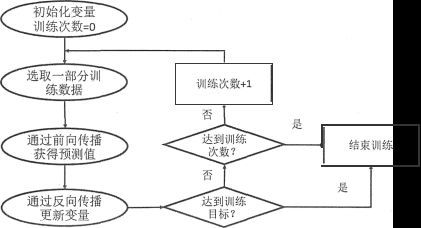
下图展示了使用反向传播算法训练神经网络的流程图:
从上图可以看出,反向传播算法实现了一个迭代的过程。在每次送代的开始,首先需要选取一小部分训练数据,这一小部分数据叫做一个 batch。然后,这个batch的样例会通过前向传播算法得到神经网络模型的预测结果。因为训练数据都是有正确答案标注的, 所以可以计算出当前神经网络模型的预测答案与正确答案之间的差距。 最后,基于这预测值和真实值之间的差距,反向传播算法会相应更新神经网络参数的取值,使得在这个 batch上神经网络模型的预测结果和真实答案更加接近。
下面给出一个完整的程序来训练神经网络解决二分类问题:
#coding=gbk
import tensorflow as tf
# Numpy是一个科学计算的工具包,这里通过Numpy工具包生成模拟数据集。
from numpy.random import RandomState
# 定义训练数据batch的大小。
batch_size=8
#定义神经网络的参数
w1 = tf.Variable(tf.random_normal([2, 3],stddev=1,seed=1))
w2 = tf.Variable(tf.random_normal([3, 1],stddev=1,seed=1))
# 在shape的一个维度上使用None可以方便使用不大的batch大小
# 在训练时需要把数据分成比较小的batch,但是在测试时,可以一次性使用全部的数据
# 当数据集比较小时这样比较方便测试
x = tf.placeholder(tf.float32,shape=(None,2), name='x-input')
y_ = tf.placeholder(tf.float32,shape=(None,1), name='y-input')
#定义神经网络前向传播的过程
a= tf.matmul(x,w1)
y = tf.matmul(a,w2)
# 定义损失函数和反向传播的算法
# cross_entropy定义了真实值和预测值之间的交又熵(cross entropy),这是分类问题中一个常用的损失函数
cross_entropy = -tf.reduce_mean(y_ * tf.log(tf.clip_by_value(y,1e-10,1.0)))
# train_step定义了反向传播的优化方法.目前TensorFlow支持7种不同的优化器。
# 比较常用的优化方法有三种:tftrain.GradientDescentOptimizer、 tftrain.AdamOptimizer 和tf.trainMomentumOptimizer
# 在定义了反向传播算法之后, 通过运行sess.run(train_step)就可以对所有在GraphKeys.TRAINABLE_VARIABLES集合中的变量进行优化
# 使得在当前batch下损失函数更小
train_step= tf.train.AdamOptimizer(0.001) .minimize(cross_entropy)
#通过随机数生成一个模拟数据集
rdm = RandomState(1)
dataset_size= 128
X= rdm.rand(dataset_size, 2)
#定义规则来给出样本的标签。在这里所有x1+x2<1的样例都被认为是正样本(比如零件合格),而其他为负样本(比如零件不合格)
#在这里使用0来表示负样本,1来表示正样本。大部分解决分类问题的神经网络都会采用0和1的表示方法
Y= [[int(x1+ x2 < 1)] for (x1, x2) in X] #列表解析式
#创建一个会话来运行 TensorFow程序。
with tf.Session() as sess:
init_op= tf.global_variables_initializer() #初始化变量
sess.run( init_op)
print("*********训练之前的初始权重weights的值:")
print(sess.run(w1) )
print(sess.run(w2))
#设定训练的轮数
STEPS = 5000
print("*******开始训练**************")
for i in range(STEPS):
#每次选取 batch_size个样本进行训练
start =(i * batch_size ) % dataset_size
end = min(start+batch_size,dataset_size)
# 通过选取的样本训练神经网络并更新参数 。
sess.run(train_step,feed_dict={x:X[start:end],y_:Y[start:end]})
if i%1000 ==0:
# 每隔一段时间计算在所有数据上的交叉熵并输出
total_cross_entropy = sess.run(cross_entropy,feed_dict={x:X, y_:Y})
print("After %d training step(s) , cross entropy on all data is %f" %(i, total_cross_entropy))
print("*******训练结束**************")
print("*********训练之后的权重weights的值:")
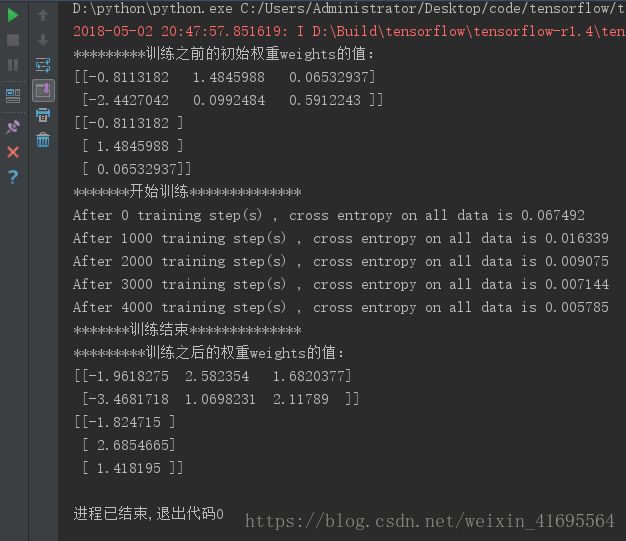
print(sess.run(w1))
print(sess.run(w2))运行程序,得到结果:
参考文献:
[1] 郑泽宇编 《TensorFlow实战Google深度学习框架》