A Comprehensive Survey on Graph Neural Networks(图神经网络综合研究)

A Comprehensive Survey on Graph Neural Networks

图神经网络综合研究

Zonghan Wu, Shirui Pan, Member, IEEE, Fengwen Chen, Guodong Long,

Chengqi Zhang, Senior Member, IEEE, Philip S. Yu, Fellow, IEEE

Abstract—Deep learning has revolutionized many machine learning tasks in recent years, ranging from image classification and video processing to speech recognition and natural language understanding. The data in these tasks are typically represented in the Euclidean space. However, there is an increasing number of applications where data are generated from non-Euclidean domains and are represented as graphs with complex relationships and interdependency between objects. The complexity of graph data has imposed significant challenges on existing machine learning algorithms. Recently, many studies on extending deep learning approaches for graph data have emerged. In this survey, we provide a comprehensive overview of graph neural networks (GNNs) in data mining and machine learning fields. We propose a new taxonomy to divide the state-of-the-art graph neural networks into different categories. With a focus on graph convolutional networks, we review alternative architectures that have recently been developed; these learning paradigms include graph attention networks, graph autoencoders, graph generative networks, and graph spatial-temporal networks. We further discuss the applications of graph neural networks across various domains and summarize the open source codes and benchmarks of the existing algorithms on different learning tasks. Finally, we propose potential research directions in this fast-growing field.

Index Terms—Deep Learning, graph neural networks, graph convolutional networks, graph representation learning, graph autoencoder, network embedding

摘要 - 深度学习近年来彻底改变了许多机器学习任务，从图像分类和视频处理到语音识别和自然语言理解。这些任务中的数据通常表示在欧几里德空间中。然而，越来越多的应用程序从非欧几里德域生成数据，并表示为具有复杂关系和对象之间相互依赖性的图。图数据的复杂性给现有的机器学习算法带来了重大挑战。最近，出现了许多关于扩展图形数据的深度学习方法的研究。在本次调查中，我们提供了数据挖掘和机器学习领域中图形神经网络（GNN）的全面概述。我们提出了一种新的分类法，将最先进的图形神经网络划分为不同的类别。我们专注于图形卷积网络，我们回顾了最近开发的替代架构;这些学习范例包括图形注意网络，图形自动编码器，图形生成网络和图形时空网络。我们进一步讨论了图神经网络在各个领域的应用，并总结了现有算法在不同学习任务中的开源代码和基准。最后，我们在这个快速发展的领域提出了潜在的研究方向。

索引术语 - 深度学习，图形神经网络，图形卷积网络，图形表示学习，图形自动编码器，网络嵌入

1 INTRODUCTION

THE recent success of neural networks has boosted re-search on pattern recognition and data mining. Many machine learning tasks such as object detection [1], [2], ma-chine translation [3], [4], and speech recognition [5], which once heavily relied on handcrafted feature engineering to extract informative feature sets, has recently been revolu-tionized by various end-to-end deep learning paradigms, i.e., convolutional neural networks (CNNs) [6], long short-term memory (LSTM) [7], and autoencoders. The success of deep learning in many domains is partially attributed to the rapidly developing computational resources (e.g., GPU) and the availability of large training data, and is partially due to the effectiveness of deep learning to extract latent representation from Euclidean data (e.g., images, text, and video). Taking image analysis as an example, an image can be represented as a regular grid in the Euclidean space. A convolutional neural network (CNN) is able to exploit the shift-invariance, local connectivity, and compositionality of image data [8], and as a result, CNN can extract local meaningful features that are shared with the entire datasets for various image analysis tasks.
While deep learning has achieved great success on Eu-clidean data, there is an increasing number of applications where data are generated from the non-Euclidean domain and need to be effectively analyzed. For instance, in e-commerce, a graph-based learning system is able to exploit the interactions between users and products [9], [10], [11] to make highly accurate recommendations. In chemistry, molecules are modeled as graphs and their bioactivity needs to be identified for drug discovery [12], [13]. In a citation network, papers are linked to each other via citations and they need to be categorized into different groups [14], [15]. The complexity of graph data has imposed significant challenges on existing machine learning algorithms. This is because graph data are irregular. Each graph has a variable size of unordered nodes and each node in a graph has a different number of neighbors, causing some important operations (e.g., convolutions), which are easy to compute in the image domain but are not directly applicable to the graph domain anymore. Furthermore, a core assumption of existing machine learning algorithms is that instances are independent of each other. However, this is not the case for graph data where each instance (node) is related to others (neighbors) via some complex linkage information, which is used to capture the interdependence among data, including citations, friendship, and interactions.

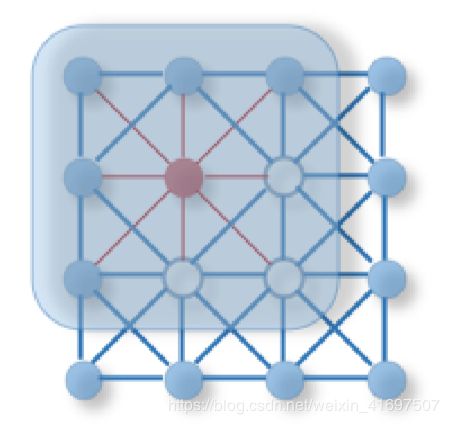
Recently, there is increasing interest in extending deep learning approaches for graph data. Driven by the success of deep learning, researchers have borrowed ideas from convolution networks, recurrent networks, and deep auto-encoders to design the architecture of graph neural networks. To handle the complexity of graph data, new gen-eralizations and definitions for important operations have been rapidly developed over the past few years. For in-stance, Figure 1 illustrates how a kind of graph convolution is inspired by a standard 2D convolution. This survey aims to provide a comprehensive overview of these methods, for both interested researchers who want to enter this rapidly developing field and experts who would like to compare graph neural network algorithms.
最近神经网络的成功推动了对模式识别和数据挖掘的重新研究。许多机器学习任务，如物体检测[1]，[2]，机器翻译[3]，[4]和语音识别[5]，曾经严重依赖手工特征工程来提取信息功能集，最近，各种端到端深度学习范例，即卷积神经网络（CNN）[6]，长期短期记忆（LSTM）[7]和自动编码器进行了革新。许多领域深度学习的成功部分归因于快速发展的计算资源（例如GPU）和大型训练数据的可用性，部分归因于深度学习从欧几里德数据中提取潜在表示的有效性（例如，图像，文字和视频）。以图像分析为例，图像可以表示为欧几里德空间中的规则网格。卷积神经网络（CNN）能够利用图像数据的移位不变性，局部连通性和组合性[8]，因此，CNN可以提取与整个数据集共享的局部有意义的特征，用于各种图像分析任务。
虽然深度学习在Eu-clidean数据上取得了巨大成功，但是越来越多的应用程序从非欧几里德域生成数据并需要进行有效分析。例如，在电子商务中，基于图形的学习系统能够利用用户和产品之间的交互[9]，[10]，[11]来制作高度准确的推荐。在化学中，分子被建模为图形，并且需要确定它们的生物活性以用于药物发现[12]，[13]。在引文网络中，论文通过引用相互联系，需要将它们分为不同的组[14]，[15]。图数据的复杂性给现有的机器学习算法带来了重大挑战。这是因为图表数据不规则。每个图都有一个可变大小的无序节点，图中的每个节点都有不同数量的邻居，导致一些重要的操作（例如卷积），这些操作很容易在图像域中计算，但不能直接应用于图域了。此外，现有机器学习算法的核心假设是实例彼此独立。然而，对于图形数据不是这种情况，其中每个实例（节点）通过一些复杂的链接信息与其他（邻居）相关，这些链接信息用于捕获数据之间的相互依赖性，包括引用，友谊和交互。

最近，人们越来越关注扩展图形数据的深度学习方法。在深度学习成功的推动下，研究人员借鉴了卷积网络，循环网络和深度自动编码器的思想，设计了图形神经网络的架构。为了处理图数据的复杂性，过去几年中，重要业务的新一代化和定义得到了迅速发展。例如，图1说明了一种图形卷积是如何受到标准2D卷积的启发。本调查旨在为想要进入这一快速发展领域的感兴趣的研究人员和想要比较图神经网络算法的专家提供这些方法的全面概述。

2 A Brief History of Graph Neural Networks The nota-tion of graph neural networks was firstly outlined in Gori et al. (2005) [16], and further elaborated in Micheli (2009) [17] and Scarselli et al. (2009) [18]. These early studies learn a target node’s representation by propagating neighbor in-formation via recurrent neural architectures in an iterative manner until a stable fixed point is reached. This process is computationally expensive, and recently there have been increasing efforts to overcome these challenges [19], [20]. In our survey, we generalize the term graph neural networks to

(a)2D Convolution. Analo-gous to a graph, each pixel in an image is taken as a node where neighbors are de-termined by the filter size. The 2D convolution takes a weighted average of pixel val-ues of the red node along with its neighbors. The neighbors of a node are ordered and have a fixed size.

(b)Graph Convolution. To get a hidden representation of the red node, one simple solution of graph convolution opera-tion takes the average value of node features of the red node along with its neighbors. Different from image data, the neighbors of a node are un-ordered and variable in size.

2图形神经网络的简史图形神经网络的概念首先在Gori等人的文章中概述。 （2005）[16]，并在Micheli（2009）[17]和Scarselli等人进一步阐述。 （2009）[18]。这些早期研究通过迭代方式通过递归神经架构传播邻居信息来学习目标节点的表示，直到达到稳定的固定点。这个过程计算成本很高，最近越来越多的努力克服这些挑战[19]，[20]。在我们的调查中，我们将术语图神经网络概括为

（a）2D卷积。对图表进行分析，图像中的每个像素都被视为一个节点，其中邻居由过滤器大小决定。 2D卷积采用红色节点及其邻居的像素值的加权平均值。节点的邻居是有序的并且具有固定的大小。

（b）图形卷积。为了获得红色节点的隐藏表示，图解卷积操作的一个简单解决方案是获取红色节点的节点特征及其邻居的平均值。与图像数据不同，节点的邻居是无序的并且大小可变。

represent all deep learning approaches for graph data. Inspired by the huge success of convolutional networks

in the computer vision domain, a large number of methods that re-define the notation of convolution for graph data have emerged recently. These approaches are under the umbrella of graph convolutional networks (GCNs). The first promi-nent research on GCNs is presented in Bruna et al. (2013), which develops a variant of graph convolution based on spectral graph theory [21]. Since that time, there have been increasing improvements, extensions, and approximations on spectral-based graph convolutional networks [12], [14], [22], [23], [24]. As spectral methods usually handle the whole graph simultaneously and are difficult to parallel or scale to large graphs, spatial-based graph convolutional networks have rapidly developed recently [25], [26], [27], [28]. These methods directly perform the convolution in the graph domain by aggregating the neighbor nodes’ informa-tion. Together with sampling strategies, the computation can be performed in a batch of nodes instead of the whole graph [25], [28], which has the potential to improve efficiency.

In addition to graph convolutional networks, many alter-native graph neural networks have been developed in the past few years. These approaches include graph attention networks, graph autoencoders, graph generative networks, and graph spatial-temporal networks. Details on the catego-rization of these methods are given in Section 3.

Related surveys on graph neural networks. There are a limited number of existing reviews on the topic of graph neural networks. Using the notation geometric deep learning, Bronstein et al. [8] give an overview of deep learning methods in the non-Euclidean domain, including graphs and manifolds. While being the first review on graph con-volution networks, this survey misses several important spatial-based approaches, including [15], [20], [25], [27], [28], [29], which update state-of-the-art benchmarks. Fur-thermore, this survey does not cover many newly devel-oped architectures which are equally important to graph convolutional networks. These learning paradigms, includ-ing graph attention networks, graph autoencoders, graph generative networks, and graph spatial-temporal networks, are comprehensively reviewed in this article. Battaglia et al. [30] position graph networks as the building blocks for learning from relational data, reviewing part of graph neu-ral networks under a unified framework. However, their generalized framework is highly abstract, losing insights on each method from its original paper. Lee et al. [31] conduct a partial survey on the graph attention model, which is one type of graph neural network. Most recently, Zhang et al. [32] present a most up-to-date survey on deep learning for graphs, missing those studies on graph generative and spatial-temporal networks. In summary, none of the existing surveys provide a comprehensive overview of graph neural networks, only covering some of the graph convolution neural networks and examining a limited number of works, thereby missing the most recent development of alternative graph neural networks, such as graph generative networks and graph spatial-temporal networks.
表示图形数据的所有深度学习方法。受到卷积网络巨大成功的启发

在计算机视觉领域，最近出现了大量重新定义图形数据卷积符号的方法。这些方法属于图卷积网络（GCN）的保护范围。关于GCN的第一个重要研究在Bruna等人的研究中提出。 （2013），它开发了基于谱图理论的图卷积变体[21]。从那时起，基于频谱的图卷积网络的改进，扩展和近似已经不断增加[12]，[14]，[22]，[23]，[24]。由于光谱方法通常同时处理整个图形并且难以与大图并行或缩放，因此基于空间的图卷积网络最近迅速发展[25]，[26]，[27]，[28]。这些方法通过聚合邻居节点的信息直接在图域中执行卷积。与采样策略一起，计算可以在一批节点中执行，而不是整个图[25]，[28]，这有可能提高效率。

除了图卷积网络之外，在过去几年中已经开发了许多替代图神经网络。这些方法包括图注意网络，图自动编码器，图生成网络和图时空网络。有关这些方法的类别化的详细信息，请参见第3节。

关于图神经网络的相关调查。关于图神经网络主题的现有评论数量有限。使用符号几何深度学习，Bronstein等。 [8]概述了非欧几里德领域的深度学习方法，包括图形和流形。虽然这是对图解卷积网络的第一次审查，但该调查错过了几种重要的基于空间的方法，包括[15]，[20]，[25]，[27]，[28]，[29]，它们更新了国家最先进的基准。此外，这项调查还没有涵盖许多新开发的架构，这些架构对于图形卷积网络同样重要。本文全面回顾了这些学习范式，包括图形注意网络，图形自动编码器，图形生成网络和图形时空网络。 Battaglia等。 [30]位置图网络作为学习关系数据的基石，在统一框架下审查图形神经网络的一部分。然而，他们的通用框架是高度抽象的，从原始论文中失去了对每种方法的见解。李等人。 [31]对图注意模型进行了部分调查，这是一种图神经网络。最近，张等人。 [32]提供了关于图的深度学习的最新调查，遗漏了关于图生成和时空网络的研究。总之，现有的调查都没有提供图神经网络的全面概述，仅覆盖一些图卷积神经网络并检查有限数量的工作，从而忽略了替代图神经网络的最新发展，如图生成网络和图形时空网络。
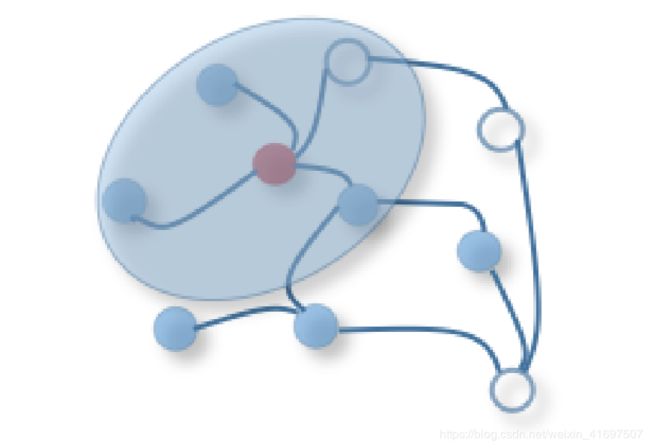
Graph neural networks vs. network embedding The research on graph neural networks is closely related to graph embedding or network embedding, another topic which attracts increasing attention from both the data min-ing and machine learning communities [33] [34] [35] [36], [37], [38]. Network embedding aims to represent network vertices into a low-dimensional vector space, by preserving both network topology structure and node content informa-tion, so that any subsequent graph analytics tasks such as classification, clustering, and recommendation can be easily performed by using simple off-the-shelf machine learning algorithm (e.g., support vector machines for classification). Many network embedding algorithms are typically unsu-pervised algorithms and they can be broadly classified into three groups [33], i.e., matrix factorization [39], [40], ran-dom walks [41], and deep learning approaches. The deep learning approaches for network embedding at the same time belong to graph neural networks, which include graph autoencoder-based algorithms (e.g., DNGR [42] and SDNE [43]) and graph convolution neural networks with unsuper-vised training(e.g., GraphSage [25]). Figure 2 describes the differences between network embedding and graph neural networks in this paper.
图形神经网络与网络嵌入图形神经网络的研究与图形嵌入或网络嵌入密切相关，另一个主题吸引了来自数据挖掘和机器学习社区的越来越多的关注[33] [34] [35] [ 36]，[37]，[38]。网络嵌入旨在通过保留网络拓扑结构和节点内容信息来将网络顶点表示为低维向量空间，以便可以通过使用简单的方式轻松执行任何后续图形分析任务，如分类，聚类和推荐现成的机器学习算法（例如，用于分类的支持向量机）。许多网络嵌入算法通常是不受限制的算法，它们可以大致分为三组[33]，即矩阵分解[39]，[40]，随机漫游[41]和深度学习方法。同时用于网络嵌入的深度学习方法属于图神经网络，其包括基于图自动编码器的算法（例如，DNGR [42]和SDNE [43]）和具有无需培训的图卷积神经网络（例如， GraphSage [25]）。图2描述了本文中网络嵌入和图神经网络之间的差异。

Fig. 1: 2D Convolution vs. Graph Convolution.

(a)2D Convolution. Analo-gous to a graph, each pixel in an image is taken as a node where neighbors are de-termined by the filter size. The 2D convolution takes a weighted average of pixel val-ues of the red node along with its neighbors. The neighbors of a node are ordered and have a fixed size.
（a）2D卷积。 对图表进行分析，图像中的每个像素都被视为一个节点，其中邻居由过滤器大小决定。 2D卷积采用红色节点及其邻居的像素值的加权平均值。 节点的邻居是有序的并且具有固定的大小。

(b)Graph Convolution. To get a hidden representation of the red node, one simple solution of graph convolution opera-tion takes the average value of node features of the red node along with its neighbors. Different from image data, the neighbors of a node are un-ordered and variable in size.

（b）图形卷积。 为了获得红色节点的隐藏表示，图解卷积操作的一个简单解决方案是获取红色节点的节点特征及其邻居的平均值。 与图像数据不同，节点的邻居是无序的并且大小可变。

Our Contributions Our paper makes notable contribu-tions summarized as follows:

New taxonomy In light of the increasing number of studies on deep learning for graph data, we propose a new taxonomy of graph neural networks (GNNs). In this taxonomy, GNNs are categorized into five groups: graph convolution networks, graph atten-tion networks, graph auto-encoders, graph genera-tive networks, and graph spatial-temporal networks. We pinpoint the differences between graph neural networks and network embedding and draw the connections between different graph neural network architectures.

Comprehensive review This survey provides the most comprehensive overview of modern deep learning techniques for graph data. For each type of graph neural network, we provide detailed de-scriptions on representative algorithms, and make a necessary comparison and summarise the corre-sponding algorithms.

Abundant resources This survey provides abundant resources on graph neural networks, which include state-of-the-art algorithms, benchmark datasets, open-source codes, and practical applications. This survey can be used as a hands-on guide for under-standing, using, and developing different deep learn-ing approaches for various real-life applications.

Future directions This survey also highlights the cur-rent limitations of the existing algorithms, and points out possible directions in this rapidly developing field.

Organization of Our Survey The rest of this survey is organized as follows. Section 2 defines a list of graph-related concepts. Section 3 clarifies the categorization of graph neural networks. Section 4 and Section 5 provides an overview of graph neural network models. Section 6 presents a gallery of applications across various domains. Section 7 discusses the current challenges and suggests future directions. Section 8 summarizes the paper.
我们的贡献我们的论文作出了显着的贡献，总结如下：

新的分类学鉴于越来越多的图形数据深度学习研究，我们提出了一种新的图神经网络分类（GNNs）。在这种分类中，GNN分为五组：图卷积网络，图形关注网络，图形自动编码器，图形生成网络和图形时空网络。我们确定了图神经网络和网络嵌入之间的差异，并绘制了不同图神经网络架构之间的联系。

综合评估本调查提供了图形数据现代深度学习技术的最全面概述。对于每种类型的图神经网络，我们提供有代表性算法的详细描述，并进行必要的比较并总结相应的算法。

丰富的资源本调查提供了丰富的图神经网络资源，包括最先进的算法，基准数据集，开源代码和实际应用。该调查可用作实践指南，用于理解，使用和开发用于各种现实应用的不同深度学习方法。

未来方向本调查还强调了现有算法的当前局限性，并指出了这一快速发展领域的可能方向。

我们的调查组织本调查的其余部分安排如下。第2节定义了与图形相关的概念列表。第3节阐明了图神经网络的分类。第4节和第5节概述了图神经网络模型。第6节介绍了各个领域的应用程序库。第7节讨论了当前的挑战并提出了未来方向。第8节总结了该论文。

2 DEFINITION

In this section, we provide definitions of basic graph con-cepts. For easy retrieval, we summarize the commonly used notations in Table 1.

图4：具有多个GCN层的图卷积网络的变体[14]。 GCN层通过聚合来自其邻居的特征信息来封装每个节点的隐藏表示。 在特征聚合之后，将非线性变换应用于结果输出。 通过堆叠多个层，每个节点的最终隐藏表示从另一个邻域接收消息。

3 CATEGORIZATION AND FRAMEWORKS

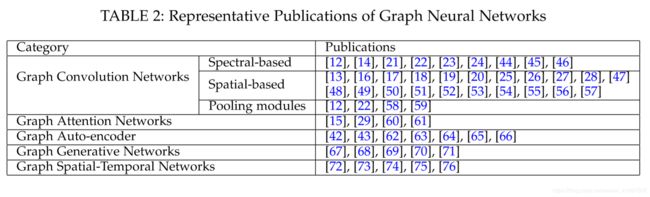
In this section, we present our taxonomy of graph neural networks. We consider any differentiable graph models which incorporate neural architectures as graph neural net-works. We categorize graph neural networks into graph con-volution networks, graph attention networks, graph auto-encoders, graph generative networks and graph spatial-temporal networks. Of these, graph convolution networks play a central role in capturing structural dependencies. As illustrated in Figure 3, methods under other categories partially utilize graph convolution networks as building blocks. We summarize the representative methods in each category in Table 2, and we give a brief introduction of each category in the following.
在本节中，我们将介绍图神经网络的分类。 我们考虑任何将神经架构作为图神经网络的可微图模型。 我们将图形神经网络分类为图形卷积网络，图形注意网络，图形自动编码器，图形生成网络和图形时空网络。 其中，图卷积网络在捕获结构依赖性方面发挥着核心作用。 如图3所示，其他类别下的方法部分地利用图卷积网络作为构建块。 我们总结了表2中每个类别的代表性方法，并在下面简要介绍了每个类别。

（a）具有用于图分类的汇集模块的图卷积网络[12]。 GCN层[14]之后是池化层，以将图形粗化为子图形，使得粗糙图形上的节点表示代表更高的图形级别表示。 为了计算每个图形标签的概率，输出层是具有SoftMax函数的线性层。

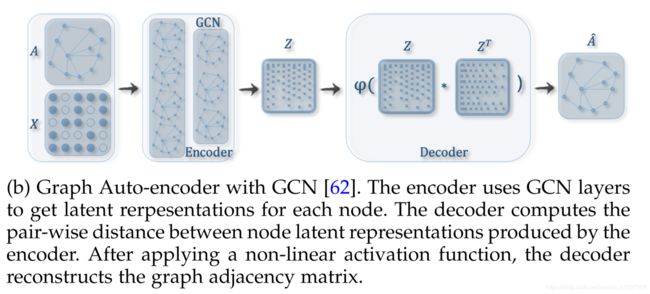
（b）带GCN的图形自动编码器[62]。 编码器使用GCN层为每个节点获得潜在的重新表示。 解码器计算编码器产生的节点潜在表示之间的成对距离。 在应用非线性激活函数之后，解码器重建图形邻接矩阵。

（c）使用GCN绘制时空网络图[74]。 GCN层之后是1D-CNN层。 GCN层在At和Xt上操作以捕获空间依赖性，而1D-CNN层沿时间轴在X上滑动以捕获时间依赖性。 输出层是线性变换，为每个节点生成预测。

图5：使用GCN构建的不同图形神经网络模型。

Taxonomy of GNNs

Graph Convolution Networks (GCNs) generalize the oper-ation of convolution from traditional data (images or grids) to graph data. The key is to learn a function f to generate a node vi’s representation by aggregating its own features Xi and neighbors’ features Xj, where j 2 N(vi). Figure 4 shows the process of GCNs for node representation learn-ing. Graph convolutional networks play a central role in building up many other complex graph neural network models, including auto-encoder-based models, generative models, and spatial-temporal networks, etc. Figure 5 illus-trates several graph neural network models building on GCNs.

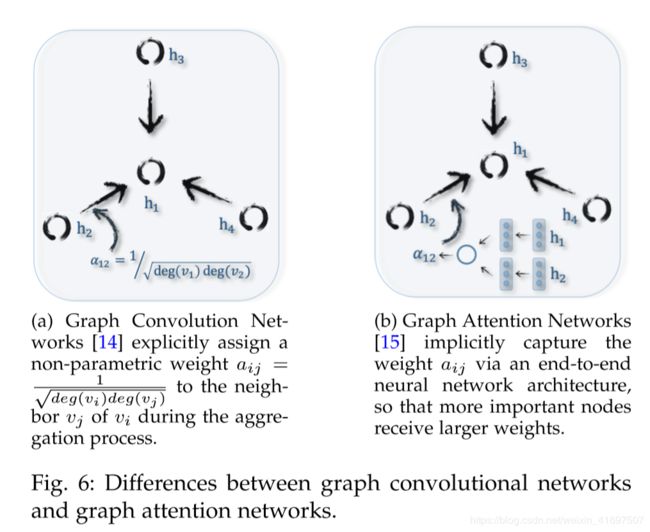
Graph Attention Networks are similar to GCNs and seek an aggregation function to fuse the neighboring nodes, random walks, and candidate models in graphs to learn a new representation. The key difference is that graph attention networks employ attention mechanisms which assign larger weights to the more important nodes, walks, or models. The attention weight is learned together with neural network

parameters within an end-to-end framework. Figure 6 illus-trates the difference between graph convolutional networks and graph attention networks in aggregating the neighbor node information.

Graph Auto-encoders are unsupervised learning frame-works which aim to learn low dimensional node vectors via an encoder, and then reconstruct the graph data via a decoder. Graph autoencoders are a popular approach to learn the graph embedding, for both plain graphs with-out attributed information [42], [43] as well as attributed graphs [64], [65]. For plain graphs, many algorithms directly prepossess the adjacency matrix, by either constructing a new matrix (i.e., pointwise mutual information matrix) with rich information [42] or feeding the adjacency matrix to an autoencoder model and capturing both first order and second order information [43]. For attributed graphs, graph autoencoder models tend to employ GCN [14] as a building block for the encoder and reconstruct the structure informa-tion via a link prediction decoder [62], [64].
图形卷积网络（GCN）概括了卷积从传统数据（图像或网格）到图形数据的操作。关键是通过聚合其自身的特征Xi和邻居的特征Xj来学习函数f以生成节点vi的表示，其中j 2 N（vi）。图4显示了节点表示学习的GCN过程。图形卷积网络在构建许多其他复杂图形神经网络模型中发挥着核心作用，包括基于自动编码器的模型，生成模型和时空网络等。图5构建基于GCN的几个图形神经网络模型。

图注意网络类似于GCN，并寻求聚合函数来融合图中的相邻节点，随机游走和候选模型以学习新的表示。关键区别在于图注意网络采用注意机制，为更重要的节点，步行或模型分配更大的权重。注意力与神经网络一起学习

端到端框架内的参数。图6示出了在聚合邻居节点信息时图形卷积网络和图形注意网络之间的差异。

图自动编码器是无监督学习框架，旨在通过编码器学习低维节点向量，然后通过解码器重建图形数据。图自动编码器是学习图嵌入的一种流行方法，对于两个没有属性信息的普通图[42]，[43]以及归因图[64]，[65]。对于普通图，许多算法通过构造具有丰富信息[42]的新矩阵（即，逐点互信息矩阵）或将邻接矩阵馈送到自动编码器模型并捕获一阶和二阶信息来直接预先存储邻接矩阵。 [43]。对于归因图，图自动编码器模型倾向于使用GCN [14]作为编码器的构建块，并通过链路预测解码器重构结构信息[62]，[64]。

Graph Generative Networks aim to generate plausible structures from data. Generating graphs given a graph empirical distribution is fundamentally challenging, mainly because graphs are complex data structures. To address this problem, researchers have explored to factor the generation process as forming nodes and edges alternatively [67], [68], to employ generative adversarial training [69], [70]. One promising application domain of graph generative networks is chemical compound synthesis. In a chemical graph, atoms are treated as nodes and chemical bonds are treated as edges. The task is to discover new synthesizable molecules which possess certain chemical and physical properties.

Graph Spatial-temporal Networks aim to learn unseen pat-terns from spatial-temporal graphs, which are increasingly important in many applications such as traffic forecasting and human activity prediction. For instance, the underlying road traffic network is a natural graph where each key loca-tion is a node whose traffic data is continuously monitored. By developing effective graph spatial-temporal network models, we can accurately predict the traffic status over the whole traffic system [73], [74]. The key idea of graph spatial-temporal networks is to consider spatial dependency and temporal dependency at the same time. Many current approaches apply GCNs to capture the dependency together with some RNN [73] or CNN [74] to model the temporal dependency.

图生成网络旨在从数据生成合理的结构。给定图形经验分布生成图形具有根本性的挑战性，主要是因为图形是复杂的数据结构。为了解决这个问题，研究人员已经探索将生成过程视为形成节点和边缘[67]，[68]，以采用生成性对抗训练[69]，[70]。图生成网络的一个有希望的应用领域是化学化合物合成。在化学图中，原子被视为节点，化学键被视为边缘。任务是发现具有某些化学和物理特性的新的可合成分子。

图时空网络旨在从空间 - 时间图中学习看不见的模式，这在许多应用中越来越重要，例如交通预测和人类活动预测。例如，基础道路交通网络是一个自然图形，其中每个关键位置是连续监测交通数据的节点。通过开发有效的图形时空网络模型，我们可以准确地预测整个交通系统的交通状况[73]，[74]。图时空网络的关键思想是同时考虑空间依赖和时间依赖。许多当前的方法应用GCN来捕获依赖性以及一些RNN [73]或CNN [74]来模拟时间依赖性。

3.2 Frameworks

Graph neural networks, graph convolution networks (GCNs) in particular, try to replicate the success of CNN in graph data by defining graph convolutions via graph spectral theory or spatial locality. With the graph structure and node content information as inputs, the outputs of GCN can focus on different graph analytics task with one of the following mechanisms:

Node-level outputs relate to node regression and classification tasks. As a graph convolution module directly gives nodes’ latent representations, a multi-perceptron layer or softmax layer is used as the final layer of GCN. We review graph convolution modules in Section 4.1 and Section 4.2.

Edge-level outputs relate to the edge classifica-tion and link prediction tasks. To predict the la-bel/connection strength of an edge, an additional function will take two nodes’ latent representations from the graph convolution module as inputs.

Graph-level outputs relate to the graph classification task. To obtain a compact representation on graph level, a pooling module is used to coarse a graph into sub-graphs or to sum/average over the node repre-sentations. We review the graph pooling module in Section 4.3.

In Table 3, we list the details of the inputs and outputs of the main GCNs methods. In particular, we summarize output mechanisms in between each GCN layer and in the final layer of each method. The output mechanisms may involve several pooling operations, which are discussed in Section 4.3.

End-to-end Training Frameworks. Graph convolutional net-works can be trained in a (semi-) supervised or purely un-supervised way within an end-to-end learning framework, depending on the learning tasks and label information avail-able at hand.

Semi-supervised learning for node-level classifi-cation. Given a single network with partial nodes being labeled and others remaining unlabeled, graph convolutional networks can learn a robust model that effectively identify the class labels for the unlabeled nodes [14]. To this end, an end-to-end framework can be built by stacking a couple of graph convolutional layers followed by a softmax layer for multi-class classification.

Supervised learning for graph-level classification. Given a graph dataset, graph-level classification aims to predict the class label(s) for an entire graph [58], [59], [77], [78]. The end-to-end learning for this task can be done with a framework which combines both graph convolutional layers and the pooling procedure [58], [59]. Specifically, by applying graph convolutional layers, we obtain representation with a fixed number of dimensions for each node in every single graph. Then, we can get the representation of an entire graph through pooling which summarizes the representation vectors of all nodes in a graph. Finally, by applying linear layers and a softmax layer, we can build an end-to-end framework for graph classification. An example is given in Fig 5a.

Unsupervised learning for graph embedding. When no class labels are available in graphs, we can learn the graph embedding in a purely unsupervised way in an end-to-end framework. These algorithms ex-ploit edge-level information in two ways. One simple way is to adopt an autoencoder framework where the encoder employs graph convolutional layers to embed the graph into the latent representation upon which a decoder is used to reconstruct the graph structure [62], [64]. Another way is to utilize the neg-ative sampling approach which samples a portion of node pairs as negative pairs while existing node pairs with links in the graphs being positive pairs. Then a logistic regression layer is applied after the convolutional layers for end-to-end learning [25].
图形神经网络，尤其是图形卷积网络（GCN），试图通过图谱理论或空间局部定义图形卷积来复制图形数据中CNN的成功。使用图形结构和节点内容信息作为输入，GCN的输出可以通过以下机制之一关注不同的图形分析任务：

节点级输出与节点回归和分类任务相关。由于图卷积模块直接给出节点的潜在表示，因此使用多感知器层或softmax层作为GCN的最后一层。我们在4.1节和4.2节中回顾图卷积模块。

边缘级输出与边缘分类和链路预测任务相关。为了预测边缘的拉贝尔/连接强度，附加函数将图形卷积模块中的两个节点的潜在表示作为输入。

图级输出与图分类任务有关。为了在图级上获得紧凑表示，使用池模块将图粗略化为子图或对节点表示求和/平均。我们将在4.3节中查看图池池模块。

在表3中，我们列出了主要GCN方法的输入和输出的详细信息。特别是，我们总结了每个GCN层之间和每个方法的最后一层之间的输出机制。输出机制可能涉及几个池操作，这将在第4.3节中讨论。

端到端培训框架。图形卷积网络可以在端到端学习框架内以（半）监督或纯粹非监督的方式进行训练，这取决于学习任务和手头有用的标签信息。

用于节点级分类的半监督学习。给定单个网络，其中部分节点被标记而其他节点未标记，图形卷积网络可以学习一个有效识别未标记节点的类标签的健壮模型[14]。为此，可以通过堆叠一对图形卷积层，然后是用于多类分类的softmax层来构建端到端框架。

用于图级分类的监督学习。给定图数据集，图级分类旨在预测整个图的类标签[58]，[59]，[77]，[78]。这项任务的端到端学习可以通过一个框架来完成，该框架结合了图形卷积层和汇集程序[58]，[59]。具体而言，通过应用图卷积层，我们获得每个图中每个节点具有固定维数的表示。然后，我们可以通过汇集来获得整个图的表示，汇总汇总图中所有节点的表示向量。最后，通过应用线性层和softmax层，我们可以构建用于图分类的端到端框架。图5a给出了一个例子。

图形嵌入的无监督学习。当图表中没有类标签时，我们可以在端到端框架中以纯粹无监督的方式学习图形嵌入。这些算法以两种方式开发边缘级信息。一种简单的方法是采用自动编码器框架，其中编码器使用图形卷积层将图形嵌入到潜在表示中，在该潜在表示上使用解码器来重建图形结构[62]，[64]。另一种方法是利用负采样方法，其将一部分节点对采样为负对，而在图中具有链路的现有节点对是正对。然后在卷积层之后应用逻辑回归层进行端到端学习[25]。

4 GRAPH CONVOLUTION NETWORKS

In this section, we review graph convolution networks (GCNs), the fundamental of many complex graph neural network models. GCNs approaches fall into two categories, spectral-based and spatial-based. Spectral-based approaches define graph convolutions by introducing filters from the perspective of graph signal processing [79] where the graph convolution operation is interpreted as removing noise from graph signals. Spatial-based approaches formulate graph convolutions as aggregating feature information from neighbors. While GCNs operate on the node level, graph pooling modules can be interleaved with the GCN layer, to coarsen graphs into high-level sub-structures. As shown in Fig 5a, such an architecture design can be used to extract graph-level representations and to perform graph classifi-cation tasks. In the following, we introduce spectral-based GCNs, spatial-based GCNs, and graph pooling modules separately.
在本节中，我们回顾图形卷积网络（GCN），这是许多复杂图形神经网络模型的基础。 GCNs方法分为两类，基于光谱和基于空间。 基于谱的方法通过从图形信号处理的角度引入滤波器来定义图形卷积[79]，其中图形卷积运算被解释为从图形信号中去除噪声。 基于空间的方法将图形卷积表示为聚合来自邻居的特征信息。 虽然GCN在节点级别上运行，但是图形池模块可以与GCN层交织，以将图形粗化为高级子结构。 如图5a所示，这种架构设计可用于提取图层级表示并执行图分类任务。 在下文中，我们分别介绍基于谱的GCN，基于空间的GCN和图池池模块。

4.1 Spectral-based Graph Convolutional Networks

Spectral-based methods have a solid foundation in graph signal processing [79]. We first give some basic knowledge background of graph signal processing, after which we review the representative research on the spectral-based GCNs.
基于光谱的方法在图形信号处理中具有坚实的基础[79]。 我们首先给出了图形信号处理的一些基本知识背景，然后我们回顾了基于光谱的GCN的代表性研究。

4.1.1 Backgrounds

In spectral-based models, graphs are assumed to be undi-rected. A robust mathematical representation of an undi-rected graph is the normalized graph Laplacian matrix,
在基于光谱的模型中，假设图形是未经修正的。 未迭代图的稳健数学表示是归一化图拉普拉斯矩阵，

result, the convolution of a graph signal x with the defined

5.3 Graph Generative Networks

The goal of graph generative networks is to generate graphs given an observed set of graphs. Many approaches to graph generative networks are domain specific. For instance, in molecular graph generation, some works model a string representation of molecular graphs called SMILES [98], [99], [100], [101]. In natural language processing, generating a se-mantic or a knowledge graph is often conditioned on a given sentence [102], [103]. Recently, several general approaches have been proposed. Some work factor the generation pro-cess as forming nodes and edges alternatively [67], [68] while others employ generative adversarial training [69], [70]. The methods in this category either employ GCN as building blocks or use different architectures.

5.3.1 GCN Based Graph Generative Networks

Molecular Generative Adversarial Networks (MolGAN) [69] integrates relational GCN [104], improved GAN [105] and reinforcement learning (RL) objective to generate graphs with desired properties. The GAN consists of a generator and a discriminator, competing with each other to improve the authenticity of the generator. In MolGAN, the generator tries to propose a faked graph along with its feature matrix while the discriminator aims to distinguish the faked sample from the empirical data. Additionally, a reward network is introduced in parallel with the dis-criminator to encourage the generated graphs to possess certain properties according to an external evaluator. The framework of MolGAN is described in Fig 9.

Deep Generative Models of Graphs (DGMG) [68] uti-lizes spatial-based graph convolution networks to obtain a hidden representation of an existing graph. The decision process of generating nodes and edges is conditioned on the resultant graph representation. Briefly, DGMG recursively proposes a node to a growing graph until a stopping crite-rion is evoked. In each step after adding a new node, DGMG repeatedly decides whether to add an edge to the added node until the decision turns to false. If the decision is true, it evaluates the probability distribution of connecting the newly added node to all existing nodes and samples one node from the probability distribution. After a new node and its connections are added to the existing graph, DGMG updates the graph representation again.

5.3.2 Miscellaneous Graph Generative Networks

GraphRNN [67] exploits deep graph generative models through two-level recurrent neural networks. The graph-level RNN adds a new node each time to a node sequence while the edge level RNN produces a binary sequence indicating connections between the newly added node and previously generated nodes in the sequence. To linearize a graph into a sequence of nodes for training the graph level RNN, GraphRNN adopts the breadth-first-search (BFS) strategy. To model the binary sequence for training the edge-level RNN, GraphRNN assumes multivariate Bernoulli or conditional Bernoulli distribution.

NetGAN [70] combines LSTM [7] with Wasserstein GAN [106] to generate graphs from a random-walk-based ap-proach. The GAN framework consists of two modules, a generator and a discriminator. The generator makes its best effort to generate plausible random walks through an LSTM network while the discriminator tries to distinguish faked random walks from the real ones. After training, a new graph is obtained by normalizing a co-occurrence matrix of nodes which occur in a set of random walks.

图9：MolGAN的框架[70]。 生成器首先从标准正态分布中采样初始向量。 通过神经网络传递该初始向量，生成器输出密集邻接矩阵A和相应的特征矩阵X.接下来，生成器基于A和X从分类分布产生采样的离散A和X.最后，GCN用于 导出采样图的矢量表示。 将该图表表示馈送到两个不同的神经网络，鉴别器和奖励网络分别输出零和一之间的分数，其将用作反馈以更新模型参数。

5.3.3 Summary

Evaluating generated graphs remains a difficult problem. Unlike synthesized images or audios, which can be di-rectly assessed by human experts, the quality of generated graphs is difficult to inspect visually. MolGAN and DGMG make use of external knowledge to evaluate the validity of generated molecule graphs. GraphRNN and NetGAN evaluate generated graphs by graph statistics (e.g. node degrees). Whereas DGMG and GraphRNN generate nodes and edges sequentially, MolGAN and NetGAN generate nodes and edges jointly. According to [71], the disadvantage of the former approaches is that when graphs become large, modeling a long sequence is not realistic. The challenge of the latter approaches is that the global properties of a graph are difficult to control. A recent approach [71] adopts variational auto-encoder to generate a graph by proposing the adjacency matrix, imposing penalty terms to address validity constraints. However, as the output space of a graph with n nodes is n2, none of these methods is scalable to large graphs.
评估生成的图形仍然是一个难题。与人类专家可以直接评估的合成图像或音频不同，生成的图形的质量难以在视觉上进行检查。 MolGAN和DGMG利用外部知识来评估生成的分子图的有效性。 GraphRNN和NetGAN通过图形统计（例如节点度）评估生成的图形。 DGMG和GraphRNN按顺序生成节点和边，而MolGAN和NetGAN共同生成节点和边。根据[71]，前一种方法的缺点是当图形变大时，对长序列建模是不现实的。后一种方法的挑战是图的全局属性难以控制。最近的方法[71]采用变分自动编码器通过提出邻接矩阵来生成图形，强加惩罚项来解决有效性约束。但是，由于具有n个节点的图的输出空间是n2，因此这些方法都不能扩展到大图。

5.4 Graph Spatial-Temporal Networks

Graph spatial-temporal networks capture spatial and tem-poral dependencies of a spatial-temporal graph simultane-ously. Spatial-temporal graphs have a global graph structure with inputs to each node which are changing across time. For instance, in traffic networks, each sensor taken as a node records the traffic speed of a certain road continuously where the edges of the traffic network are determined by the distance between pairs of sensors. The goal of graph spatial-temporal networks can be forecasting future node values or labels, or predicting spatial-temporal graph labels. Recent studies have explored the use of GCNs [75] solely, a combination of GCNs with RNN [73] or CNN [74], and a recurrent architecture tailored to graph structures [76]. In the following, we introduce these methods.

图形时空网络同时捕获空间 - 时间图的空间和时间依赖性。 时空图具有全局图结构，每个节点的输入随时间变化。 例如，在交通网络中，作为节点的每个传感器连续地记录某个道路的交通速度，其中交通网络的边缘由传感器对之间的距离确定。 图形时空网络的目标可以是预测未来的节点值或标签，或预测时空图标签。 最近的研究仅探讨了GCN [75]的使用，GCN与RNN [73]或CNN [74]的结合，以及针对图形结构定制的循环架构[76]。 在下文中，我们介绍这些方法。

7 FUTURE DIRECTIONS

Though graph neural networks have proven their power in learning graph data, challenges still exist due to the complexity of graphs. In this section, we provide four future directions of graph neural networks.

Go Deep The success of deep learning lies in deep neu-ral architectures. In image classification, for example, an outstanding model named ResNet [153] has 152 layers. However, when it comes to graphs, experimental studies have shown that with the increase in the number of layers, the model performance drops dramatically [110]. According to [110], this is due to the effect of graph convolutions in that it essentially pushes representations of adjacent nodes closer to each other so that, in theory, with an infinite times of convolutions, all nodes’ representations will converge to a single point. This raises the question of whether going deep is still a good strategy for learning graph-structured data.

Receptive Field The receptive field of a node refers to a set of nodes including the central node and its neighbors. The number of neighbors of a node follows a power law distribution. Some nodes may only have one neighbor, while other nodes may neighbors as many as thousands. Though sampling strategies have been adopted [25], [27], [28], how to select a representative receptive field of a node remains to be explored.

Scalability Most graph neural networks do not scale well for large graphs. The main reason for this is when stacking multiple layers of a graph convolution, a node’s final state involves a large number of its neighbors’ hidden states, leading to the high complexity of backpropagation. While several approaches try to improve their model efficiency by fast sampling [48], [49] and sub-graph training [25], [28], they are still not scalable enough to handle deep architec-tures with large graphs.

Dynamics and Heterogeneity The majority of current graph neural networks tackle with static homogeneous graphs. On the one hand, graph structures are assumed to be fixed. On the other hand, nodes and edges from a graph are assumed to come from a single source. However, these two assumptions are not realistic in many scenarios. In a social
虽然图形神经网络已经证明了它们在学习图形数据方面的能力，但由于图形的复杂性，仍然存在挑战。在本节中，我们提供了图神经网络的四个未来方向。

深入了解深度学习的成功在于深层的神经架构。例如，在图像分类中，名为ResNet [153]的优秀模型具有152个层。然而，当谈到图表时，实验研究表明，随着层数的增加，模型性能急剧下降[110]。根据[110]，这是由于图形卷积的影响，它基本上推动了相邻节点的表示彼此更接近，因此理论上，无限次卷积时，所有节点的表示将收敛到单个点。这提出了一个问题，即深入研究是否仍然是学习图形结构数据的好策略。

接收字段节点的接收字段是指包括中心节点及其邻居的一组节点。节点的邻居数量遵循幂律分布。一些节点可能只有一个邻居，而其他节点可能有多达几千个邻居。虽然采用了采样策略[25]，[27]，[28]，但如何选择节点的代表性感受野仍有待探索。

可伸缩性大多数图形神经网络对于大型图形都不能很好地扩展。其主要原因是当堆叠图层卷积的多个层时，节点的最终状态涉及其大量邻居的隐藏状态，导致反向传播的高度复杂性。虽然有几种方法试图通过快速采样[48]，[49]和子图训练[25]，[28]来提高模型效率，但它们仍然不具有足够的可扩展性来处理具有大图的深层架构。

动力学和异质性大多数当前的图神经网络都采用静态齐次图来处理。一方面，假设图形结构是固定的。另一方面，假设图中的节点和边来自单个源。然而，在许多情况下，这两个假设是不现实的。在社交中

• JOURNAL OF LATEX CLASS FILES, VOL. X, NO. X, DECEMBER 2018

network, a new person may enter into a network at any time and an existing person may quit the network as well. In a recommender system, products may have different types where their inputs may have different forms such as texts or images. Therefore, new methods should be developed to handle dynamic and heterogeneous graph structures.
在网络中，新人可以随时进入网络，现有人也可以退出网络。 在推荐系统中，产品可以具有不同的类型，其输入可以具有不同的形式，例如文本或图像。 因此，应该开发新的方法来处理动态和异构图结构。

8 CONCLUSION

In this survey, we conduct a comprehensive overview of graph neural networks. We provide a taxonomy which groups graph neural networks into five categories: graph convolutional networks, graph attention networks, graph autoencoders, graph generative networks and graph spatial-temporal networks. We provide a thorough review, com-parisons, and summarizations of the methods within or between categories. Then we introduce a wide range of ap-plications of graph neural networks. Datasets, open source codes, and benchmarks for graph neural networks are sum-marized. Finally, we suggest four future directions for graph neural networks.
在本次调查中，我们对图神经网络进行了全面的概述。 我们提供了一种分类法，将图形神经网络分为五类：图形卷积网络，图形注意网络，图形自动编码器，图形生成网络和图形时空网络。 我们提供对类别内或类别之间方法的全面审查，比较和总结。 然后我们介绍了图神经网络的广泛应用。 总结了图形神经网络的数据集，开源代码和基准。 最后，我们建议图形神经网络的四个未来方向。

ACKNOWLEDGMENT

This research was funded by the Australian Government through the Australian Research Council (ARC) under grants 1) LP160100630 partnership with Australia Govern-ment Department of Health and 2) LP150100671 partnership with Australia Research Alliance for Children and Youth (ARACY) and Global Business College Australia (GBCA). We acknowledge the support of NVIDIA Corporation and MakeMagic Australia with the donation of GPU used for this research.
该研究由澳大利亚政府通过澳大利亚研究委员会（ARC）资助，1）LP160100630与澳大利亚政府卫生部合作，2）LP150100671与澳大利亚儿童和青年研究联盟（ARACY）和全球商业学院合作 澳大利亚（GBCA）。 我们感谢NVIDIA公司和MakeMagic Australia的支持，并捐赠了用于本研究的GPU。

REFERENCES

[1]J. Redmon, S. Divvala, R. Girshick, and A. Farhadi, “You only look once: Unified, real-time object detection,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 779–788.

[2]S. Ren, K. He, R. Girshick, and J. Sun, “Faster r-cnn: Towards real-time object detection with region proposal networks,” in Advances in neural information processing systems, 2015, pp. 91–99.
[3]M.-T. Luong, H. Pham, and C. D. Manning, “Effective approaches to attention-based neural machine translation,” in Proceedings of the Conference on Empirical Methods in Natural Language Processing, 2015, pp. 1412–1421.

[4]Y. Wu, M. Schuster, Z. Chen, Q. V. Le, M. Norouzi, W. Macherey, M. Krikun, Y. Cao, Q. Gao, K. Macherey et al., “Google’s neural machine translation system: Bridging the gap between human and machine translation,” arXiv preprint arXiv:1609.08144, 2016.

[5]G. Hinton, L. Deng, D. Yu, G. E. Dahl, A.-r. Mohamed, N. Jaitly, A. Senior, V. Vanhoucke, P. Nguyen, T. N. Sainath et al., “Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups,” IEEE Signal processing magazine, vol. 29, no. 6, pp. 82–97, 2012.

[6]Y. LeCun, Y. Bengio et al., “Convolutional networks for images, speech, and time series,” The handbook of brain theory and neural networks, vol. 3361, no. 10, p. 1995, 1995.

[7]S. Hochreiter and J. Schmidhuber, “Long short-term memory,” Neural computation, vol. 9, no. 8, pp. 1735–1780, 1997.

[8]M. M. Bronstein, J. Bruna, Y. LeCun, A. Szlam, and P. Van-dergheynst, “Geometric deep learning: going beyond euclidean data,” IEEE Signal Processing Magazine, vol. 34, no. 4, pp. 18–42, 2017.

[9]R. van den Berg, T. N. Kipf, and M. Welling, “Graph convolu-tional matrix completion,” stat, vol. 1050, p. 7, 2017.
[10]F. Monti, M. Bronstein, and X. Bresson, “Geometric matrix com-pletion with recurrent multi-graph neural networks,” in Advances in Neural Information Processing Systems, 2017, pp. 3697–3707.

19

[11]R. Ying, R. He, K. Chen, P. Eksombatchai, W. L. Hamilton, and

J.Leskovec, “Graph convolutional neural networks for web-scale recommender systems,” in Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 2018, pp. 974–983.

[12]M. Defferrard, X. Bresson, and P. Vandergheynst, “Convolutional neural networks on graphs with fast localized spectral filtering,” in Advances in Neural Information Processing Systems, 2016, pp. 3844–3852.

[13]J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals, and G. E. Dahl, “Neural message passing for quantum chemistry,” in Proceedings of the International Conference on Machine Learning, 2017, pp. 1263– 1272.

[14]T. N. Kipf and M. Welling, “Semi-supervised classification with graph convolutional networks,” in Proceedings of the International Conference on Learning Representations, 2017.

[15]P. Velickovic, G. Cucurull, A. Casanova, A. Romero, P. Lio, and Y. Bengio, “Graph attention networks,” in Proceedings of the International Conference on Learning Representations, 2017.

[16]M. Gori, G. Monfardini, and F. Scarselli, “A new model for learning in graph domains,” in Proceedings of the International Joint Conference on Neural Networks, vol. 2. IEEE, 2005, pp. 729–734.
[17]A. Micheli, “Neural network for graphs: A contextual construc-tive approach,” IEEE Transactions on Neural Networks, vol. 20, no. 3, pp. 498–511, 2009.
[18]F. Scarselli, M. Gori, A. C. Tsoi, M. Hagenbuchner, and G. Mon-fardini, “The graph neural network model,” IEEE Transactions on Neural Networks, vol. 20, no. 1, pp. 61–80, 2009.

[19]Y. Li, D. Tarlow, M. Brockschmidt, and R. Zemel, “Gated graph sequence neural networks,” in Proceedings of the International Conference on Learning Representations, 2015.

[20]H. Dai, Z. Kozareva, B. Dai, A. Smola, and L. Song, “Learning steady-states of iterative algorithms over graphs,” in Proceedings of the International Conference on Machine Learning, 2018, pp. 1114– 1122.

[21]J. Bruna, W. Zaremba, A. Szlam, and Y. LeCun, “Spectral net-works and locally connected networks on graphs,” in Proceedings of International Conference on Learning Representations, 2014.
[22]M. Henaff, J. Bruna, and Y. LeCun, “Deep convolutional networks on graph-structured data,” arXiv preprint arXiv:1506.05163, 2015.
[23]R. Li, S. Wang, F. Zhu, and J. Huang, “Adaptive graph convolu-tional neural networks,” in Proceedings of the AAAI Conference on Artificial Intelligence, 2018, pp. 3546–3553.

[24]R. Levie, F. Monti, X. Bresson, and M. M. Bronstein, “Cayleynets: Graph convolutional neural networks with complex rational spectral filters,” IEEE Transactions on Signal Processing, vol. 67, no. 1, pp. 97–109, 2017.

[25]W. Hamilton, Z. Ying, and J. Leskovec, “Inductive representation learning on large graphs,” in Advances in Neural Information Processing Systems, 2017, pp. 1024–1034.

[26]F. Monti, D. Boscaini, J. Masci, E. Rodola, J. Svoboda, and M. M. Bronstein, “Geometric deep learning on graphs and manifolds using mixture model cnns,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017, pp. 5115–5124.

[27]M. Niepert, M. Ahmed, and K. Kutzkov, “Learning convolutional neural networks for graphs,” in Proceedings of the International Conference on Machine Learning, 2016, pp. 2014–2023.

[28]H. Gao, Z. Wang, and S. Ji, “Large-scale learnable graph convolu-tional networks,” in Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. ACM, 2018, pp. 1416–1424.

[29]J. Zhang, X. Shi, J. Xie, H. Ma, I. King, and D.-Y. Yeung, “Gaan: Gated attention networks for learning on large and spatiotem-poral graphs,” in Proceedings of the Uncertainty in Artificial Intelli-gence, 2018.
[30]P. W. Battaglia, J. B. Hamrick, V. Bapst, A. Sanchez-Gonzalez,
V.Zambaldi, M. Malinowski, A. Tacchetti, D. Raposo, A. Santoro,

R.Faulkner et al., “Relational inductive biases, deep learning, and graph networks,” arXiv preprint arXiv:1806.01261, 2018.
[31]J. B. Lee, R. A. Rossi, S. Kim, N. K. Ahmed, and E. Koh, “Attention models in graphs: A survey,” arXiv preprint arXiv:1807.07984, 2018.
[32]Z. Zhang, P. Cui, and W. Zhu, “Deep learning on graphs: A survey,” arXiv preprint arXiv:1812.04202, 2018.
[33]P. Cui, X. Wang, J. Pei, and W. Zhu, “A survey on network em-bedding,” IEEE Transactions on Knowledge and Data Engineering, 2017.

JOURNAL OF LATEX CLASS FILES, VOL. X, NO. X, DECEMBER 2018

[34]W. L. Hamilton, R. Ying, and J. Leskovec, “Representation learn-ing on graphs: Methods and applications,” in Advances in Neural Information Processing Systems, 2017, pp. 1024–1034.

[35]D. Zhang, J. Yin, X. Zhu, and C. Zhang, “Network representation learning: A survey,” IEEE Transactions on Big Data, 2018.

[36]H. Cai, V. W. Zheng, and K. Chang, “A comprehensive survey of graph embedding: problems, techniques and applications,” IEEE Transactions on Knowledge and Data Engineering, 2018.

[37]P. Goyal and E. Ferrara, “Graph embedding techniques, applica-tions, and performance: A survey,” Knowledge-Based Systems, vol. 151, pp. 78–94, 2018.
[38]S. Pan, J. Wu, X. Zhu, C. Zhang, and Y. Wang, “Tri-party deep network representation,” in Proceedings of the International Joint Conference on Artificial Intelligence. AAAI Press, 2016, pp. 1895– 1901.

[39]X. Shen, S. Pan, W. Liu, Y.-S. Ong, and Q.-S. Sun, “Discrete network embedding,” in Proceedings of the International Joint Con-ference on Artificial Intelligence, 7 2018, pp. 3549–3555.

[40]H. Yang, S. Pan, P. Zhang, L. Chen, D. Lian, and C. Zhang, “Binarized attributed network embedding,” in IEEE International Conference on Data Mining. IEEE, 2018.

[41]B. Perozzi, R. Al-Rfou, and S. Skiena, “Deepwalk: Online learning of social representations,” in Proceedings of the ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, 2014, pp. 701–710.

[42]S. Cao, W. Lu, and Q. Xu, “Deep neural networks for learning graph representations,” in Proceedings of the AAAI Conference on Artificial Intelligence, 2016, pp. 1145–1152.

[43]D. Wang, P. Cui, and W. Zhu, “Structural deep network embed-ding,” in Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 2016, pp. 1225– 1234.

[44]A. Sandryhaila and J. M. Moura, “Discrete signal processing on graphs,” IEEE transactions on signal processing, vol. 61, no. 7, pp. 1644–1656, 2013.
[45]S. Chen, R. Varma, A. Sandryhaila, and J. Kovaceviˇc,´ “Discrete signal processing on graphs: Sampling theory,” IEEE Transactions on Signal Processing, vol. 63, no. 24, pp. 6510–6523, 2015.

[46]A. Susnjara, N. Perraudin, D. Kressner, and P. Vandergheynst, “Accelerated filtering on graphs using lanczos method,” arXiv preprint arXiv:1509.04537, 2015.
[47]J. Atwood and D. Towsley, “Diffusion-convolutional neural net-works,” in Advances in Neural Information Processing Systems, 2016, pp. 1993–2001.
[48]J. Chen, T. Ma, and C. Xiao, “Fastgcn: fast learning with graph convolutional networks via importance sampling,” in Proceedings of the International Conference on Learning Representations, 2018.

[49]J. Chen, J. Zhu, and L. Song, “Stochastic training of graph convolutional networks with variance reduction,” in Proceedings of the International Conference on Machine Learning, 2018, pp. 941– 949.

[50]F. P. Such, S. Sah, M. A. Dominguez, S. Pillai, C. Zhang, A. Michael, N. D. Cahill, and R. Ptucha, “Robust spatial filter-ing with graph convolutional neural networks,” IEEE Journal of Selected Topics in Signal Processing, vol. 11, no. 6, pp. 884–896, 2017.

[51]Z. Liu, C. Chen, L. Li, J. Zhou, X. Li, and L. Song, “Geniepath: Graph neural networks with adaptive receptive paths,” arXiv preprint arXiv:1802.00910, 2018.
[52]C. Zhuang and Q. Ma, “Dual graph convolutional networks for graph-based semi-supervised classification,” in Proceedings of the World Wide Web Conference on World Wide Web. International World Wide Web Conferences Steering Committee, 2018, pp. 499– 508.

[53]T. Derr, Y. Ma, and J. Tang, “Signed graph convolutional net-work,” arXiv preprint arXiv:1808.06354, 2018.

[54]T. Pham, T. Tran, D. Q. Phung, and S. Venkatesh, “Column networks for collective classification,” in Proceedings of the AAAI Conference on Artificial Intelligence, 2017, pp. 2485–2491.

[55]M. Simonovsky and N. Komodakis, “Dynamic edgeconditioned filters in convolutional neural networks on graphs,” in Proceed-ings of the IEEE conference on computer vision and pattern recognition, 2017.

[56]S. Kearnes, K. McCloskey, M. Berndl, V. Pande, and P. Riley, “Molecular graph convolutions: moving beyond fingerprints,”

• Journal of computer-aided molecular design, vol. 30, no. 8, pp. 595– 608, 2016.

[57]W. Huang, T. Zhang, Y. Rong, and J. Huang, “Adaptive sampling towards fast graph representation learning,” in Advances in Neu-ral Information Processing Systems, 2018, pp. 4563–4572.

[58]M. Zhang, Z. Cui, M. Neumann, and Y. Chen, “An end-to-end deep learning architecture for graph classification,” in Proceedings of the AAAI Conference on Artificial Intelligence, 2018.

[59]Z. Ying, J. You, C. Morris, X. Ren, W. Hamilton, and J. Leskovec, “Hierarchical graph representation learning with differentiable pooling,” in Advances in Neural Information Processing Systems, 2018, pp. 4801–4811.

[60]J. B. Lee, R. Rossi, and X. Kong, “Graph classification using struc-tural attention,” in Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. ACM, 2018,

ap.1666–1674.
[61]S. Abu-El-Haija, B. Perozzi, R. Al-Rfou, and A. A. Alemi, “Watch your step: Learning node embeddings via graph attention,” in

Advances in Neural Information Processing Systems, 2018, pp. 9197– 9207.

[62]T. N. Kipf and M. Welling, “Variational graph auto-encoders,” arXiv preprint arXiv:1611.07308, 2016.

[63]C. Wang, S. Pan, G. Long, X. Zhu, and J. Jiang, “Mgae: Marginal-ized graph autoencoder for graph clustering,” in Proceedings of the ACM on Conference on Information and Knowledge Management. ACM, 2017, pp. 889–898.

[64]S. Pan, R. Hu, G. Long, J. Jiang, L. Yao, and C. Zhang, “Adver-sarially regularized graph autoencoder for graph embedding.” in Proceedings of the International Joint Conference on Artificial Intelligence, 2018, pp. 2609–2615.

[65]W. Yu, C. Zheng, W. Cheng, C. C. Aggarwal, D. Song, B. Zong, H. Chen, and W. Wang, “Learning deep network representations with adversarially regularized autoencoders,” in Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. ACM, 2018, pp. 2663–2671.

[66]K. Tu, P. Cui, X. Wang, P. S. Yu, and W. Zhu, “Deep recursive network embedding with regular equivalence,” in Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 2018, pp. 2357–2366.

[67]J. You, R. Ying, X. Ren, W. L. Hamilton, and J. Leskovec, “Graphrnn: A deep generative model for graphs,” Proceedings of International Conference on Machine Learning, 2018.

[68]Y. Li, O. Vinyals, C. Dyer, R. Pascanu, and P. Battaglia, “Learning deep generative models of graphs,” in Proceedings of the Interna-tional Conference on Machine Learning, 2018.

[69]N. De Cao and T. Kipf, “Molgan: An implicit generative model for small molecular graphs,” arXiv preprint arXiv:1805.11973, 2018.
[70]A. Bojchevski, O. Shchur, D. Zugner,¨ and S. Gunnemann,¨ “Net-gan: Generating graphs via random walks,” in Proceedings of the International Conference on Machine Learning, 2018.

[71]T. Ma, J. Chen, and C. Xiao, “Constrained generation of semanti-cally valid graphs via regularizing variational autoencoders,” in
Advances in Neural Information Processing Systems, 2018, pp. 7110– 7121.

[72]Y. Seo, M. Defferrard, P. Vandergheynst, and X. Bresson, “Struc-tured sequence modeling with graph convolutional recurrent networks,” arXiv preprint arXiv:1612.07659, 2016.
[73]Y. Li, R. Yu, C. Shahabi, and Y. Liu, “Diffusion convolutional recurrent neural network: Data-driven traffic forecasting,” in

Proceedings of International Conference on Learning Representations, 2018.

[74]B. Yu, H. Yin, and Z. Zhu, “Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting,” in Proceedings of the International Joint Conference on Artificial Intelligence, 2018, pp. 3634–3640.

[75]S. Yan, Y. Xiong, and D. Lin, “Spatial temporal graph con-volutional networks for skeleton-based action recognition,” in

Proceedings of the AAAI Conference on Artificial Intelligence, 2018.
[76]A. Jain, A. R. Zamir, S. Savarese, and A. Saxena, “Structural-rnn: Deep learning on spatio-temporal graphs,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016,

ap.5308–5317.
[77]S. Pan, J. Wu, X. Zhu, C. Zhang, and P. S. Yu, “Joint structure feature exploration and regularization for multi-task graph clas-sification,” IEEE Transactions on Knowledge and Data Engineering, vol. 28, no. 3, pp. 715–728, 2016.

[78]S. Pan, J. Wu, X. Zhu, G. Long, and C. Zhang, “Task sensitive fea-ture exploration and learning for multitask graph classification,”

IEEE transactions on cybernetics, vol. 47, no. 3, pp. 744–758, 2017.

JOURNAL OF LATEX CLASS FILES, VOL. X, NO. X, DECEMBER 2018

[79]D. I. Shuman, S. K. Narang, P. Frossard, A. Ortega, and P. Van-dergheynst, “The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains,” IEEE Signal Processing Magazine, vol. 30, no. 3, pp. 83–98, 2013.

[80]L. B. Almeida, “A learning rule for asynchronous perceptrons with feedback in a combinatorial environment.” in Proceedings of the International Conference on Neural Networks, vol. 2. IEEE, 1987,

ap.609–618.
[81]F. J. Pineda, “Generalization of back-propagation to recurrent neural networks,” Physical review letters, vol. 59, no. 19, p. 2229, 1987.
[82]K. Cho, B. Van Merrienboer,¨ C. Gulcehre, D. Bahdanau, F. Bougares, H. Schwenk, and Y. Bengio, “Learning phrase rep-resentations using rnn encoder-decoder for statistical machine translation,” in Proceedings of the Conference on Empirical Methods in Natural Language Processing, 2014, pp. 1724–1734.
[83]D. K. Duvenaud, D. Maclaurin, J. Iparraguirre, R. Bombarell, T. Hirzel, A. Aspuru-Guzik, and R. P. Adams, “Convolutional networks on graphs for learning molecular fingerprints,” in
Advances in Neural Information Processing Systems, 2015, pp. 2224– 2232.

[84]K. T. Schutt,¨ F. Arbabzadah, S. Chmiela, K. R. Muller,¨ and A. Tkatchenko, “Quantum-chemical insights from deep tensor neural networks,” Nature communications, vol. 8, p. 13890, 2017.

[85]B. Weisfeiler and A. Lehman, “A reduction of a graph to a canonical form and an algebra arising during this reduction,”

Nauchno-Technicheskaya Informatsia, vol. 2, no. 9, pp. 12–16, 1968.
[86]B. L. Douglas, “The weisfeiler-lehman method and graph isomor-phism testing,” arXiv preprint arXiv:1101.5211, 2011.

[87]J. Masci, D. Boscaini, M. Bronstein, and P. Vandergheynst, “Geodesic convolutional neural networks on riemannian mani-folds,” in Proceedings of the IEEE International Conference on Com-puter Vision Workshops, 2015, pp. 37–45.

[88]D. Boscaini, J. Masci, E. Rodola,` and M. Bronstein, “Learning shape correspondence with anisotropic convolutional neural net-works,” in Advances in Neural Information Processing Systems, 2016,

ap.3189–3197.
[89]M. Fey, J. E. Lenssen, F. Weichert, and H. Muller,¨ “Splinecnn: Fast geometric deep learning with continuous b-spline kernels,” in

Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 869–877.

[90]D. V. Tran, A. Sperduti et al., “On filter size in graph convolu-tional networks,” in 2018 IEEE Symposium Series on Computational Intelligence (SSCI). IEEE, 2018, pp. 1534–1541.

[91]S. Pan, J. Wu, and X. Zhu, “Cogboost: Boosting for fast cost-sensitive graph classification,” IEEE Transactions on Knowledge & Data Engineering, no. 1, pp. 1–1, 2015.

[92]K. Xu, W. Hu, J. Leskovec, and S. Jegelka, “How powerful are graph neural networks,” arXiv preprint arXiv:1810.00826, 2018.

[93]S. Verma and Z.-L. Zhang, “Graph capsule convolutional neural networks,” arXiv preprint arXiv:1805.08090, 2018.

[94]A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser, and I. Polosukhin, “Attention is all you need,” in Advances in Neural Information Processing Systems, 2017, pp. 5998–6008.

[95]I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville, and Y. Bengio, “Generative adver-sarial nets,” in Advances in neural information processing systems, 2014, pp. 2672–2680.

[96]I. Sutskever, O. Vinyals, and Q. V. Le, “Sequence to sequence learning with neural networks,” in Advances in Neural Information Processing Systems, 2014, pp. 3104–3112.
[97]P. Vincent, H. Larochelle, Y. Bengio, and P.-A. Manzagol, “Ex-tracting and composing robust features with denoising autoen-coders,” in Proceedings of the international conference on Machine learning. ACM, 2008, pp. 1096–1103.

[98]G. L. Guimaraes, B. Sanchez-Lengeling, C. Outeiral, P. L. C. Farias, and A. Aspuru-Guzik, “Objective-reinforced generative adversarial networks (organ) for sequence generation models,” arXiv preprint arXiv:1705.10843, 2017.

[99]M. J. Kusner, B. Paige, and J. M. Hernandez´-Lobato, “Grammar variational autoencoder,” arXiv preprint arXiv:1703.01925, 2017.

[100]H. Dai, Y. Tian, B. Dai, S. Skiena, and L. Song, “Syntax-directed variational autoencoder for molecule generation,” in Proceedings of the International Conference on Learning Representations, 2018.

[101]R. Gomez´-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernandez´-Lobato, B. Sanchez´-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams, and A. Aspuru-Guzik, “Automatic chemical design using a data-driven continuous representation of molecules,” ACS central science, vol. 4, no. 2, pp. 268–276, 2018.
[102]B. Chen, L. Sun, and X. Han, “Sequence-to-action: End-to-end semantic graph generation for semantic parsing,” in Proceedings of the Annual Meeting of the Association for Computational Linguistics, 2018, pp. 766–777.

[103]D. D. Johnson, “Learning graphical state transitions,” in Proceed-ings of the International Conference on Learning Representations, 2016.

[104]M. Schlichtkrull, T. N. Kipf, P. Bloem, R. van den Berg, I. Titov, and M. Welling, “Modeling relational data with graph convolu-tional networks,” in European Semantic Web Conference. Springer, 2018, pp. 593–607.

[105]I. Gulrajani, F. Ahmed, M. Arjovsky, V. Dumoulin, and A. C. Courville, “Improved training of wasserstein gans,” in Advances in Neural Information Processing Systems, 2017, pp. 5767–5777.

[106]M. Arjovsky, S. Chintala, and L. Bottou, “Wasserstein gan,” arXiv preprint arXiv:1701.07875, 2017.

[107]P. Sen, G. Namata, M. Bilgic, L. Getoor, B. Galligher, and T. Eliassi-Rad, “Collective classification in network data,” AI magazine, vol. 29, no. 3, p. 93, 2008.
[108]X. Zhang, Y. Li, D. Shen, and L. Carin, “Diffusion maps for textual network embedding,” in Advances in Neural Information Processing Systems, 2018.

[109]P. Velickoviˇc,´ W. Fedus, W. L. Hamilton, P. Lio,` Y. Ben-gio, and R. D. Hjelm, “Deep graph infomax,” arXiv preprint arXiv:1809.10341, 2018.
[110]Q. Li, Z. Han, and X.-M. Wu, “Deeper insights into graph convo-lutional networks for semi-supervised learning,” in Proceedings of the AAAI Conference on Artificial Intelligence, 2018.

[111]J. Tang, J. Zhang, L. Yao, J. Li, L. Zhang, and Z. Su, “Arnetminer: extraction and mining of academic social networks,” in Proceed-ings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 2008, pp. 990–998.

[112]Y. Ma, S. Wang, C. C. Aggarwal, D. Yin, and J. Tang, “Multi-dimensional graph convolutional networks,” arXiv preprint arXiv:1808.06099, 2018.
[113]L. Tang and H. Liu, “Relational learning via latent social dimen-sions,” in Proceedings of the ACM SIGKDD International Conference on Knowledge Ciscovery and Data Mining. ACM, 2009, pp. 817– 826.

[114]H. Wang, J. Wang, J. Wang, M. Zhao, W. Zhang, F. Zhang, X. Xie, and M. Guo, “Graphgan: Graph representation learning with generative adversarial nets,” in Proceedings of the AAAI Conference on Artificial Intelligence, 2017.

[115]M. Zitnik and J. Leskovec, “Predicting multicellular function through multi-layer tissue networks,” Bioinformatics, vol. 33, no. 14, pp. i190–i198, 2017.
[116]N. Wale, I. A. Watson, and G. Karypis, “Comparison of descrip-tor spaces for chemical compound retrieval and classification,”

Knowledge and Information Systems, vol. 14, no. 3, pp. 347–375, 2008.

[117]A. K. Debnath, R. L. Lopez de Compadre, G. Debnath, A. J. Shusterman, and C. Hansch, “Structure-activity relationship of mutagenic aromatic and heteroaromatic nitro compounds. cor-relation with molecular orbital energies and hydrophobicity,” Journal of medicinal chemistry, vol. 34, no. 2, pp. 786–797, 1991.
[118]P. D. Dobson and A. J. Doig, “Distinguishing enzyme structures from non-enzymes without alignments,” Journal of molecular biol-ogy, vol. 330, no. 4, pp. 771–783, 2003.
[119]R. Ramakrishnan, P. O. Dral, M. Rupp, and O. A. Von Lilien-feld, “Quantum chemistry structures and properties of 134 kilo molecules,” Scientific data, vol. 1, p. 140022, 2014.
[120]T. Joachims, “A probabilistic analysis of the rocchio algorithm with tfidf for text categorization.” Carnegie-mellon univ pitts-burgh pa dept of computer science, Tech. Rep., 1996.

[121]H. Jagadish, J. Gehrke, A. Labrinidis, Y. Papakonstantinou, J. M. Patel, R. Ramakrishnan, and C. Shahabi, “Big data and its tech-nical challenges,” Communications of the ACM, vol. 57, no. 7, pp. 86–94, 2014.

[122]B. N. Miller, I. Albert, S. K. Lam, J. A. Konstan, and J. Riedl, “Movielens unplugged: experiences with an occasionally con-nected recommender system,” in Proceedings of the international conference on Intelligent user interfaces. ACM, 2003, pp. 263–266.

JOURNAL OF LATEX CLASS FILES, VOL. X, NO. X, DECEMBER 2018

[123]A. Carlson, J. Betteridge, B. Kisiel, B. Settles, E. R. Hruschka Jr, and T. M. Mitchell, “Toward an architecture for never-ending language learning.” in Proceedings of the AAAI Conference on Artificial Intelligence, 2010, pp. 1306–1313.

[124]M. Zhang and Y. Chen, “Link prediction based on graph neural networks,” in Advances in Neural Information Processing Systems, 2018.
[125]T. Kawamoto, M. Tsubaki, and T. Obuchi, “Mean-field theory of graph neural networks in graph partitioning,” in Advances in Neural Information Processing Systems, 2018, pp. 4362–4372.

[126]D. Xu, Y. Zhu, C. B. Choy, and L. Fei-Fei, “Scene graph generation by iterative message passing,” in Proceedings of the IEEE Confer-ence on Computer Vision and Pattern Recognition, vol. 2, 2017.
[127]J. Yang, J. Lu, S. Lee, D. Batra, and D. Parikh, “Graph r-cnn for scene graph generation,” in European Conference on Computer Vision. Springer, 2018, pp. 690–706.

[128]Y. Li, W. Ouyang, B. Zhou, J. Shi, C. Zhang, and X. Wang, “Fac-torizable net: an efficient subgraph-based framework for scene graph generation,” in European Conference on Computer Vision. Springer, 2018, pp. 346–363.

[129]J. Johnson, A. Gupta, and L. Fei-Fei, “Image generation from scene graphs,” arXiv preprint, 2018.
[130]Y. Wang, Y. Sun, Z. Liu, S. E. Sarma, M. M. Bronstein, and J. M. Solomon, “Dynamic graph cnn for learning on point clouds,” arXiv preprint arXiv:1801.07829, 2018.

[131]L. Landrieu and M. Simonovsky, “Large-scale point cloud seman-tic segmentation with superpoint graphs,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018.
[132]G. Te, W. Hu, Z. Guo, and A. Zheng, “Rgcnn: Regular-ized graph cnn for point cloud segmentation,” arXiv preprint arXiv:1806.02952, 2018.

[133]S. Qi, W. Wang, B. Jia, J. Shen, and S.-C. Zhu, “Learning human-object interactions by graph parsing neural networks,” in Proceed-ings of the European Conference on Computer Vision (ECCV), 2018,
ap.401–417.
[134]V. G. Satorras and J. B. Estrach, “Few-shot learning with graph neural networks,” in Proceedings of the International Conference on Learning Representations, 2018.

[135]M. Guo, E. Chou, D.-A. Huang, S. Song, S. Yeung, and L. Fei-Fei, “Neural graph matching networks for fewshot 3d action recognition,” in European Conference on Computer Vision. Springer, 2018, pp. 673–689.

[136]X. Qi, R. Liao, J. Jia, S. Fidler, and R. Urtasun, “3d graph neural networks for rgbd semantic segmentation,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017,
ap.5199–5208.
[137]L. Yi, H. Su, X. Guo, and L. J. Guibas, “Syncspeccnn: Synchro-nized spectral cnn for 3d shape segmentation.” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017, pp. 6584–6592.

[138]X. Chen, L.-J. Li, L. Fei-Fei, and A. Gupta, “Iterative visual reason-ing beyond convolutions,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018.

[139]M. Narasimhan, S. Lazebnik, and A. Schwing, “Out of the box: Reasoning with graph convolution nets for factual visual

22

question answering,” in Advances in Neural Information Processing Systems, 2018, pp. 2655–2666.

[140]Z. Cui, K. Henrickson, R. Ke, and Y. Wang, “High-order graph convolutional recurrent neural network: a deep learning frame-work for network-scale traffic learning and forecasting,” arXiv preprint arXiv:1802.07007, 2018.

[141]H. Yao, F. Wu, J. Ke, X. Tang, Y. Jia, S. Lu, P. Gong, J. Ye, and Z. Li, “Deep multi-view spatial-temporal network for taxi demand prediction,” in Proceedings of the AAAI Conference on Artificial Intelligence, 2018, pp. 2588–2595.

[142]J. Tang, M. Qu, M. Wang, M. Zhang, J. Yan, and Q. Mei, “Line: Large-scale information network embedding,” in Proceedings of the International Conference on World Wide Web. International World Wide Web Conferences Steering Committee, 2015, pp. 1067–1077.

[143]A. Fout, J. Byrd, B. Shariat, and A. Ben-Hur, “Protein interface prediction using graph convolutional networks,” in Advances in Neural Information Processing Systems, 2017, pp. 6530–6539.

[144]J. You, B. Liu, R. Ying, V. Pande, and J. Leskovec, “Graph convolutional policy network for goal-directed molecular graph generation,” in Advances in Neural Information Processing Systems, 2018.

[145]M. Allamanis, M. Brockschmidt, and M. Khademi, “Learning to represent programs with graphs,” in Proceedings of the Interna-tional Conference on Learning Representations, 2017.
[146]J. Qiu, J. Tang, H. Ma, Y. Dong, K. Wang, and J. Tang, “Deepinf: Social influence prediction with deep learning,” in Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. ACM, 2018, pp. 2110–2119.

[147]D. Zugner,¨ A. Akbarnejad, and S. Gunnemann,¨ “Adversarial attacks on neural networks for graph data,” in Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 2018, pp. 2847–2856.

[148]E. Choi, M. T. Bahadori, L. Song, W. F. Stewart, and J. Sun, “Gram: graph-based attention model for healthcare representation learn-ing,” in Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 2017, pp. 787–795.

[149]E. Choi, C. Xiao, W. Stewart, and J. Sun, “Mime: Multilevel medical embedding of electronic health records for predictive healthcare,” in Advances in Neural Information Processing Systems, 2018, pp. 4548–4558.

[150]J. Kawahara, C. J. Brown, S. P. Miller, B. G. Booth, V. Chau, R. E. Grunau, J. G. Zwicker, and G. Hamarneh, “Brainnetcnn: convo-lutional neural networks for brain networks; towards predicting neurodevelopment,” NeuroImage, vol. 146, pp. 1038–1049, 2017.

[151]T. H. Nguyen and R. Grishman, “Graph convolutional networks with argument-aware pooling for event detection,” in Proceedings of the AAAI Conference on Artificial Intelligence, 2018, pp. 5900– 5907.

[152]Z. Li, Q. Chen, and V. Koltun, “Combinatorial optimization with graph convolutional networks and guided tree search,” in Advances in Neural Information Processing Systems, 2018, pp. 536– 545.

[153]K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778.