实验一 信号、系统及系统响应
文章目录
- 实验目的
- 实验原理
实验目的
1、了解常用的时域离散信号及其特点;
2、掌握Matlab产生常用时域离散信号的方法;
3、掌握时域离散信号简单的基本运算方法。
4、掌握求解离散时间系统冲激响应和阶跃响应的方法;
5、进一步理解卷积定理,掌握应用线性卷积求解离散时间系统响应的基本方法;
6、掌握离散系统的响应特点。
实验原理
1、常用序列
单位脉冲序列(单位抽样)、单位阶跃序列、矩形序列、实指数序列、复指数序列、正弦型序列等。
(1)单位脉冲序列
方法一
n1=-5:5; %显然,用逻辑式是比较高明的方法
x1=[(n1-0)==0];;%逻辑判断,自动循环,满条件置1.
stem(n1,x1);%作用是绘制以n1为横坐标,x1为纵坐标的离散杆图title(单位脉冲序列)
title('单位脉冲序列')%绘制标题
axis([-5 5 0 1]);%横坐标从-5到5,纵坐标从0到1
x=[1 zeros(1,N-1)]%产生长度为N的单位脉冲序列
(2)单位阶跃序列
clear;
n1=-5:5;
x1=[n1>=0];%逻辑判断,自动循环,满条件置1.
stem(n1,x1);%作用是绘制以n1为横坐标,x1为纵坐标的离散杆图title(单位脉冲序列)
title('单位阶跃序列')%绘制标题
axis([-5 5 0 1]);%横坐标从-5到5,纵坐标从0到1

2、序列的基本运算
(1)序列的移位y(n)=x(n-k)
在这个运算中,x(n)的每一个样本都向右移动k个采样周期。实际上, x(n-k)取的是序列过去的值,具有物理可实现性;而x(n+k) 要知道序列未来的值,物理上无法直接实现。所以数字信号处理中通常都用序列右移。
clc;clear;
n=-3:10;k0=3;k1=-3;
x=cos(2*pi*n/10);%原始信号
x1=cos(2*pi*(n-k0)/10);
x2=cos(2*pi*(n-k1)/10);
subplot(311),stem(n,x,'filled','r');%填充红色
ylabel('x(n)');
subplot(312),stem(n,x1,'filled','b');%填充蓝色
ylabel('x(n-2)');
subplot(313),stem(n,x2,'k');%无填充黑色
ylabel('x(n+2)');

(2)序列相加x(n)=x1(n)+x2(n)
当序列x1(n)和x2(n)的长度不等或位置不对应时,首先应使两者位置对齐, 然后通过zeros函数左右补零使其长度相等后再相加。
(3) 序列相乘:x(n)=x1(n) x2(n)
序列的乘法是一种非线性运算,它用于信号的调制。它把两个序列中位 置序号相同的样本相乘,形成新的样本序列。
在MATLAB中序列加法可用算术运算符“+”实现,序列乘 法要用点乘运算符“.*”实现。然后首先必须使x1和x2的位置向 量的起点、终点相同,长度相等。
clc;clear;
x1=[0 1 2 3 4 3 2 1 0];ns1=-2;
x2=[2 2 0 0 0 -2 -2];ns2=2;
nf1=ns1+length(x1)-1;nf2=ns2+length(x2)-1;
ny=min(ns1,ns2):max(nf1,nf2);
xa1=zeros(1,length(ny));xa2=xa1;
xa1(find((ny>=ns1)&(ny<=nf1)==1))=x1;
xa2(find((ny>=ns2)&(ny<=nf2)==1))=x2;
ya = xa1 + xa2 % 序列相加
yp = xa1.* xa2 % 序列相乘
subplot(4,1,1), stem(ny,xa1,'.') % 绘图
subplot(4,1,2), stem(ny,xa2,'.')
line([ny(1),ny(end)],[0,0]) % 画x轴
subplot(4,1,3), stem(ny,ya,'.')
line([ny(1),ny(end)],[0,0])
subplot(4,1,4), stem(ny,yp,'.')
line([ny(1),ny(end)],[0,0])

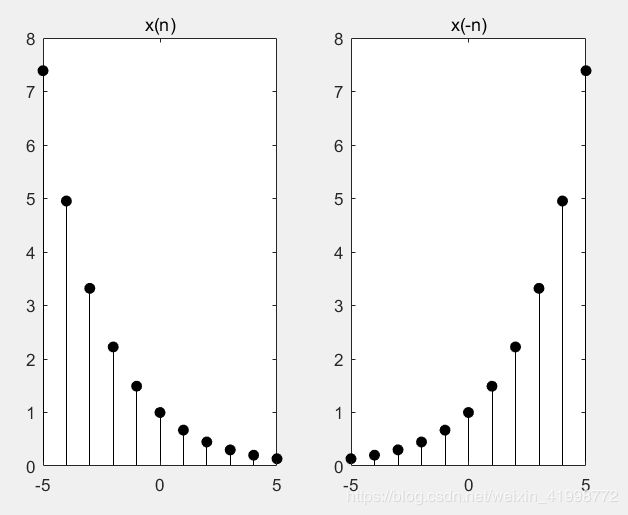
(4)序列的反转:y(n)=x(-n)
在这个运算中,x(n)的每一个样本都对纵坐标轴n=0做对称翻转(flip-flop)得 到反转后的序列。在MATLAB中,这一运算要两次调用fliplr函数来实现。 y=fliplr(x)的作用是把行向量x中元素排列的次序左右翻转。ny=-fliplr(nx)既将其
位置向量左右翻转,又变了正负号。
程序:
y = fliplr(x); % 将序列数值左右翻转
ny = -fliplr(nx); % 将序列位置对零位置左右翻转,故同时改变正负号
n=-5:5;
x=exp(-0.4*n);
x1=fliplr(x);
n1=-fliplr(n);
subplot(1,2,1),stem(n,x,'filled','k');title('x(n)');
subplot(1,2,2),stem(n1,x1,'filled','k');title('x(-n)');
3、系统响应求解
(1)用impz和dstep函数求解离散系统的单位冲激响应和阶跃响应
例:零状态因果系统的差分方程为y(n)+0.5y(n1)=x(n)+2x(n-2)
a=[1,0.5,0]; b=[1,0,2]; %系数向量
n=16;
hn=impz(b,a,n); %冲激响应
gn=dstep(b,a,n); %阶跃响应
(2)用conv函数进行卷积计算