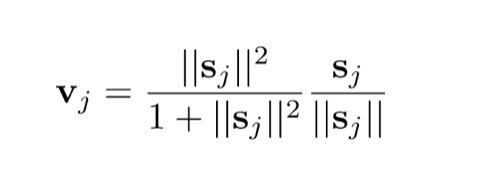关于胶囊网络(Capsule Net)的个人理解
最近在跟踪keras的contri版的更新时,发现了冒出了一个Capsule层。于是我百度+谷歌一顿操作猛如虎,才发现在很早之前,胶囊网络的概念就提出了。但是限于胶囊网络的performance并不是在各个数据集都是碾压的情况,并且其计算量偏大,训练时间偏长,所以并没有被广泛的运用和替换。但是在官方给出的测试结果来看,其实效果还是挺不错的。
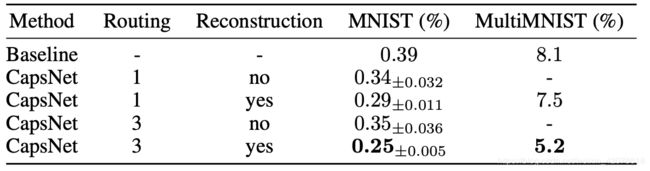
以上是原论文(https://arxiv.org/pdf/1710.09829.pdf)在mnist是数据集上的结果,结果是指错误率,可见效果还是有小幅提升的。在介绍胶囊网络之前,给大家推荐一篇博客,写得很好。https://www.jiqizhixin.com/articles/2017-11-05。同时,在keras上有开发者提供的capsule层源码:https://github.com/keras-team/keras-contrib/blob/master/keras_contrib/layers/capsule.py。本文将会以该源码为主,从各大博客的角度以及个人观点介绍胶囊网络。
另外,欢迎大家看看我之前介绍的bert模型 https://blog.csdn.net/weixin_42078618/article/details/94394348,两者在层的设计上游异曲同工之处
一、什么是胶囊网络?
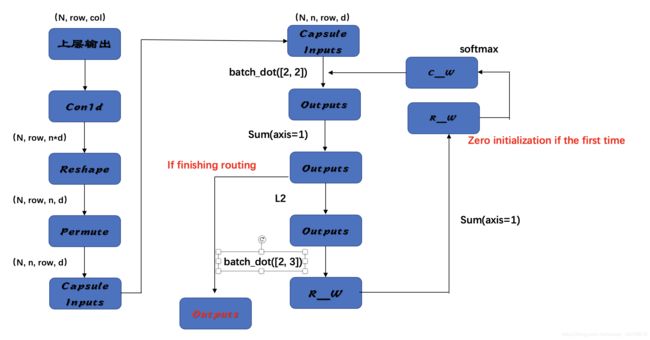
看看博客中的一张图,简单明了。
简而言之就是,我有一个权重(叫做胶囊权重),它来来回回地跟输入数据做计算,一边计算一边更新自己(路由算法)。
步骤如下:
(1)我先对胶囊层上一层的数据先做个预处理,处理前需要一个权重来为处理做计算过度,这个权重就是![]() ,处理成胶囊层需要的数据结构,即:
,处理成胶囊层需要的数据结构,即:![]() (1号标)。所以这里的
(1号标)。所以这里的![]() 是指胶囊层上一层的输出,即将囊层的输入。真正的胶囊层计算从
是指胶囊层上一层的输出,即将囊层的输入。真正的胶囊层计算从![]() 开始
开始
(2)接着,我又定义了(或计算出)一组权重![]() (2号标),跟
(2号标),跟![]() 作矩阵乘法,得到
作矩阵乘法,得到![]() (3号标),重复此步。
(3号标),重复此步。
(3)然后,对![]() 做激活,得到
做激活,得到![]() (4号标)
(4号标)
OVER!
看到这,我相信很多人还是一头雾水,当时我也是一头雾水。。。屮艸芔茻。。。于是我去读了一遍keras的源码和官方example,我才发现,其实,跟这个还是有点区别的。咱们再看一个keras官方的实现逻辑。
二、胶囊网络的结构
首先,我们假设上一层的数据输入是N x 72 x 64(N个句子,每个句子最多72个字,每个字的嵌入维度是64)的一个数据格式,胶囊数为5,胶囊输出维度为10,路由次数为4
(1)生成过度权重
# (1, 72, 5*10)
self.W = self.add_weight(name='capsule_kernel',
shape=(1,
input_dim_capsule,
self.num_capsule *
self.dim_capsule),
initializer=self.initializer,
regularizer=self.regularizer,
constraint=self.constraint,
trainable=True)
# (N, 72, 64) conv1d (1, 64, 50) --->>> (N, 72, 50)
u_hat_vectors = K.conv1d(inputs, self.W)为什么说他是过度权重呢?
首先,该层传入的数据,它不符合计算的数据格式,需要对它做一些调整。
比如:这层需要做一个3行5列的矩阵跟一个5行7列的矩阵做矩阵乘法,但是我输入的数据是3行6列的,怎么办?这里作者使用了卷积,把3行6列卷成3行5列。
怎么卷?一维卷积!相当于用了50个channel=64的1x1的卷积核做卷积,这里一定要想明白。相当于keras的Conv1D
那为什么不用Dense(全连接层)?也可以,当然可以。但是卷积的参数量小嘛,并且可以减少过拟合的风险,当然这里我个人认为用全连接也未尝不可,可能效果没有卷积好。
其次,如上所说,用全连接也可以达到这个效果,用池化行不行?也行!所以这步本质上只是一个过渡,过渡到胶囊核心计算所要求的数据格式。
到此,咱们的数据变成(N, 72, 50)的结构
(2)调整胶囊结构
# (N, 72, 5, 10)
u_hat_vectors = K.reshape(u_hat_vectors, (batch_size,
input_num_capsule,
self.num_capsule,
self.dim_capsule))
# (N, 72, 5, 10) --->>> (N, 5, 72, 10)
u_hat_vectors = K.permute_dimensions(u_hat_vectors, (0, 2, 1, 3))这两句怎么理解呢?我们可以看成该数据有N个句子,每个句子最大72个字,每个字由5个胶囊单元组成,每个单元包含10个维度的抽象信息。
我们把该数据组合做一下转置,转成:N个句子,每个句子由5个胶囊单元组成,每个胶囊单元由72个字组成,每个字包含10个维度的抽象信息。
到这步,你会发现,这步操作跟自注意力的多头机制是一模一样的、一模一样的、一模一样的!了解过多头自注意力的看官,接下里看着感觉就是炒多头的旧饭!
(3)初始化一个胶囊权重
routing_weights = K.zeros_like(u_hat_vectors[:, :, :, 0])这个权重会贯穿整个胶囊单元的计算
(4)胶囊单元计算(路由算法)
1)softmax调整权重
capsule_weights = K.softmax(routing_weights, 1)这一步可以先跳过,待会回头来看这一步
2)打分机制
# (N, 5, 72) * (N, 5, 72, 10) --->>> (N, 5, 5, 10)
outputs = K.batch_dot(capsule_weights, u_hat_vectors, [2, 2])这一步,又跟多头自注意力是一致的。唯一的区别是,多头自注意力是互相打分,而这里的胶囊计算是一个人给其他所有人打分!胶囊权重参数跟每一个channel的胶囊单元进行矩阵乘法,即:打分!
3)对胶囊个数所在维度进行求和
if K.ndim(outputs) == 4:
# (N, 5, 10)
outputs = K.sum(outputs, axis=1)这是根据论文的原意进行的计算操作。这一步个人感觉,主要是为了把数据继续拉回符合下一步计算的格式。你说用K.mean可不可以,用K.max可不可以,我觉得似乎问题都不大。
4)L2正则。常规减少过拟合操作
outputs = K.l2_normalize(outputs, -1)5)再一次打分机制!
# (N, 5, 5, 72)
routing_weights = K.batch_dot(outputs, u_hat_vectors, [2, 3])这一次的矩阵乘法维度是[2, 3],这次设计打分是对胶囊单元的维度进行打分
看到这里,你还敢说跟多头自注意力机制不像?
6)继续求和,拉回到初始胶囊单元的数据格式
if K.ndim(routing_weights) == 4:
# (N, 5, 72)
routing_weights = K.sum(routing_weights, axis=1)到这,那简直就是多头自注意力模型的变体。他俩几乎一模一样。
我们先回顾一下,多头自注意力模型的核心过程。
a、对输入数据做拆分,分成QKV的前身
b、对QKV进行多头拆分
c、Q跟K互相打分--->>>得到W
d、W跟V互相打分--->>>得到O
e、对O进行多头合并
g、如此循环b——e,便可以形成深层多头自注意力模型
咱们再回顾一下胶囊网络的核心过程。
a、对输入数据做一维卷积,得到胶囊输入U的前身
b、路由权重W跟胶囊输入U打分,求和得到输出O
c、输出O跟胶囊输入U打分,求和更新路由权重W
d、重复b——c,便可以形成深层路由层
所以,仔细想想,真正实现出来的胶囊网络跟论文以及上篇博客论述的胶囊网络,还是有点差异的。这里我把我从源码读出来的胶囊网络跟大家分享一下
中间的核心计算层,他简直就是自注意力层的一个缩小版!!!
r_w表示路由权重,c_w表示胶囊权重,他们都只是一个权重在不同阶段的状态罢了。
他跟自注意力层的区别有两大点:
1、打分机制不同。attention一致都是自己跟自己打分- -,且同一维度跟同一维度打分;而胶囊网络是设置一个可学习的单维权重(相对胶囊输入数据而言是单维的),跟多维的输入数据进行数据维度一对多的打分,在跟胶囊维度一对多的打分。
2、激活函数不同。胶囊网络使用squash激活函数,attention使用gelu和relu。
三、其他
1、squash激活函数
公式如下:
简单吧!给大家看看图长什么样。
画面真是不能太舒服。。。
这个公式主要由两个式子构成,左边和右边。。。其中s是指向量
左边:向量二范式的平方 / 向量二范式的平方 + 1,说白了就是![]()
右边:单位向量嘛
所以这个公式既保证了数据在0-1之间,也保留了向量的方向(可以理解为数据在另一个维度的特征)。
2、损失函数
Margin loss
啊,这里不展开了
四、总结
原来这就是胶囊网络。看过bert源码的,对这个胶囊结构应该是一见如故吧,它俩可真是太像了,设计理念是异曲同工的,各类预测结果还都让人眼前一亮。
对于胶囊网络,个人觉得,对于数据的结构操作,不太适合做图像的backbone。因为胶囊输入需要的是N, row, col三维数据,这就必然导致三维图像(N, row, col, chanel)需要做reshape操作,这一操作,讲不准损失了什么图像的空间信息。
总之,胶囊网络是读完了,不造给位看官是否还有点雾水上头啊。