《TensorFlow 深度学习》阅读笔记（三）—— 神经网络

二、神经网络

---

注：整理自《TensorFlow 深度学习》(龙龙老师)一书，侵删

1. 神经网络组成

   

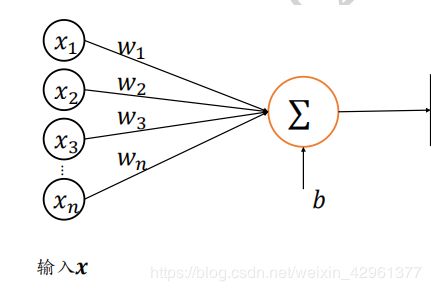
   神经元模型如上图，X为输入的向量，W为超参数向量，b为偏置项。输出的计算公式如下：
   $$y=\sum _{i=1}^n{x}_i{w}_i$$
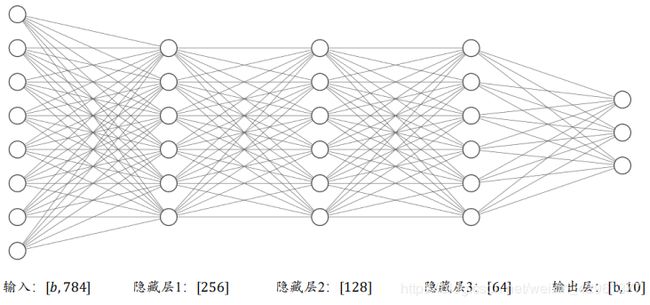
   多个神经元，可以构成神经网络，如下图：

中间部分称为隐藏层，神经网络层数在计算的时候只计算隐藏层及输出层。

2. 神经网络的实现

   对于上述的神经网络有两种方式实现：

   • 张量方式

   # 隐藏层 1 张量
   w1 = tf.Variable(tf.random.truncated_normal([784, 256], stddev=0.1))
   b1 = tf.Variable(tf.zeros([256]))
   # 隐藏层 2 张量
   w2 = tf.Variable(tf.random.truncated_normal([256, 128], stddev=0.1))
   b2 = tf.Variable(tf.zeros([128]))
   # 隐藏层 3 张量
   w3 = tf.Variable(tf.random.truncated_normal([128, 64], stddev=0.1))
   b3 = tf.Variable(tf.zeros([64]))
   # 输出层张量
   w4 = tf.Variable(tf.random.truncated_normal([64, 10], stddev=0.1))
   b4 = tf.Variable(tf.zeros([10]))
   
   .
   .
   .
   
   # 计算的时候（前向传播）
   with tf.GradientTape() as tape: # 梯度记录器
       # x: [b, 28*28]
    	# 隐藏层 1 前向计算，[b, 28*28] => [b, 256]
    	h1 = x@w1 + tf.broadcast_to(b1, [x.shape[0], 256])
    	h1 = tf.nn.relu(h1) # 输出通过激活函数
    	# 隐藏层 2 前向计算，[b, 256] => [b, 128]
    	h2 = h1@w2 + b2
    	h2 = tf.nn.relu(h2)
    	# 隐藏层 3 前向计算，[b, 128] => [b, 64] 
    	h3 = h2@w3 + b3
    	h3 = tf.nn.relu(h3)
    	# 输出层前向计算，[b, 64] => [b, 10] 
    	h4 = h3@w4 + b4
   

   • 层方式实现

   fc1 = layers.Dense(256, activation=tf.nn.relu) # 隐藏层 1
   fc2 = layers.Dense(128, activation=tf.nn.relu) # 隐藏层 2
   fc3 = layers.Dense(64, activation=tf.nn.relu) # 隐藏层 3
   fc4 = layers.Dense(10, activation=None) # 输出层
   
   .
   .
   .
   
   # 计算的时候（前向传播）
   with tf.GradientTape() as tape: # 梯度记录器
   	x = tf.random.normal([4,28*28])
   	h1 = fc1(x) # 通过隐藏层 1 得到输出
   	h2 = fc2(h1) # 通过隐藏层 2 得到输出
   	h3 = fc3(h2) # 通过隐藏层 3 得到输出
   	h4 = fc4(h3) # 通过输出层得到网络输出
   

   上述层方式，各层在定义后，可以将各层按顺序放入列表之中，在将列表放入模型容器。计算的时候，将输入的观测值传入模型容器即可。如下：

   model = layers.Sequential([
       layers.Dense(256, activation=tf.nn.relu) , # 创建隐藏层 1
    	layers.Dense(128, activation=tf.nn.relu) , # 创建隐藏层 2
    	layers.Dense(64, activation=tf.nn.relu) , # 创建隐藏层 3
    	layers.Dense(10, activation=None) , # 创建输出层
   ])
   
   #计算过程(前向传播)
   with tf.GradientTape() as tape: # 梯度记录器
       x = tf.random.normal([4,28*28])
       out = model(x)
   

3. 前向传播过程

   前向传播即从输入开始，通过各神经网络层，最后得到输出的过程。其最后一步就是完成误差的计算：
   $$\mathcal{L}=g(f_{\theta }(x),y)$$
   其中$f_{\theta }(\bullet )$代表了利用参数化的神经网络模型，$g(\bullet )$称之为误差函数，用来描述当前网络的
   预测值$f_{\theta }(\bullet )$与真实标签y之间的差距度量，比如常用的均方差误差函数，ℒ称为网络的误差
   (Error，或损失 Loss)，一般为标量。

   训练的目标即为在训练集上寻找一组能够使得损失函数朝着所期望的方向变化的最好的超参数。

4. 激活函数

   前向传播过程经常需要将观测值通过神经网络层输出之后，再通过一个激活函数，以获得观测值的非线性信息。常用的激活函数有：

   • Sigmoid

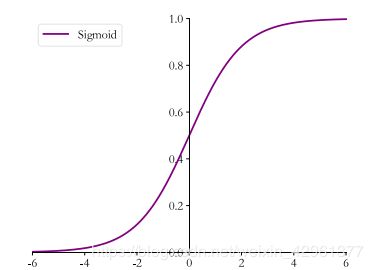
     Sigmoid 函数也叫 Logistic 函数，定义为：
     $$Sigmoid:=\frac{1}{1+e^{-x}}$$
     其图像如下：

     

     它的一个优良特性就是能够把 ∈ 的输入“压缩”到 ∈ [0,1]区间，这个区间的数值在机器学习常用来表示以下意义:

     • 概率分布 [0,1]区间的输出和概率的分布范围契合，可以通过 Sigmoid 函数将输出转译为概率输出。
     • 信号强度 一般可以将 0~1 理解为某种信号的强度，如像素的颜色强度，1 代表当前通道颜色最强，0 代表当前通道无颜色；抑或代表门控值(Gate)的强度，1 代表当前门控全部开放，0 代表门控关闭。

   • ReLU

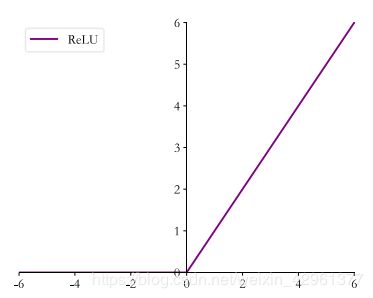
     ReLU定义如下：
     $$ReLU(x):=\max (0,x)$$
     其图像如下：

   

   在 ReLU(REctified Linear Unit，修正线性单元)激活函数提出之前，Sigmoid 函数通常是神经网络的激活函数首选。但是 Sigmoid 函数在输入值较大或较小时容易出现梯度值接近于 0 的现象，称为梯度弥散现象，网络参数长时间得不到更新，很难训练较深层次的网络模型。

   除了可以使用函数式接口 tf.nn.relu实现 ReLU 函数外，还可以像 Dense 层一样将ReLU 函数作为一个网络层添加到网络中，对应的类为 layers.ReLU()类。一般来说，激活函数类并不是主要的网络运算层，不计入网络的层数。

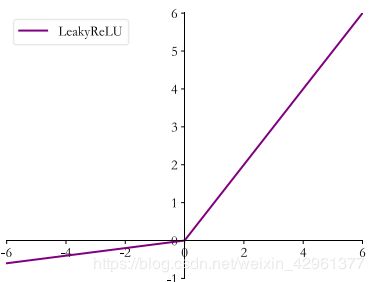
   • LeakyReLU

     LeakyReLU 表达式为:
     $$LeakyReLU=\{\begin{array}{l}x,x\ge 0\\ p\ast x,x<0\end{array}$$
     其图像如下：

     

     其中为用户自行设置的某较小数值的超参数，如 0.02 等。当 = 0时，LeayReLU 函数退化为 ReLU 函数；当 ≠ 0时， < 0能够获得较小的梯度值，从而避免出现梯度弥散现象。

     tf.nn.leaky_relu 对应的类为 layers.LeakyReLU，可以通过LeakyReLU(alpha)创建 LeakyReLU 网络层，并设置参数，像 Dense 层一样将LeakyReLU层放置在网络的合适位置。

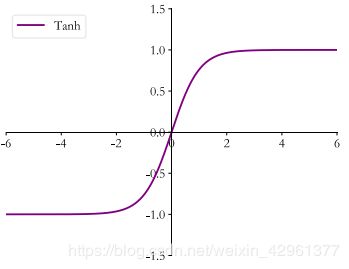
   • Tanh

     Tanh 函数能够将 ∈ 的输入“压缩”到[−1,1]区间，定义为：
     $$\begin{gathered} tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}} \\ =2\ast sigmoid(2x)-1 \end{gathered}$$
     可以看到 tanh 激活函数可通过 Sigmoid 函数缩放平移后实现，函数曲线如下：

     

     可以通过 tf.nn.tanh 实现 tanh 函数。

5. 输出层的设计

   常见的几种输出类型包括：

   • $o\in R^d$ 输出属于整个实数空间，或者某段普通的实数空间，比如函数值趋势的预测，年龄的预测问题等。

   • ∈ [0,1] 输出值特别地落在[0, 1]的区间，如图片生成，图片像素值一般用[0, 1]表示；或者二分类问题的概率，如硬币正反面的概率预测问题。

     对于二分类问题，如硬币的正反面的预测，输出层可以只需要一个节点，表示某个事件 A 发生的概率P(|)。只需要在输出层的净活性值 z 后添加 Sigmoid 函数即可将输出转译为概率值。

   • ∈ [0,  1],${\sum }_i{o}_i=1$输出值落在[0, 1]的区间，并且所有输出值之和为 1，常见的如多分类问题，如 MNIST 手写数字图片识别，图片属于 10 个类别的概率之和为 1。

     可以通过在输出层添加 Softmax 函数实现。Softmax 函数定义为：
     $$\sigma (z_i)=\frac{e^{z_i}}{{\sum }_{j=1}^{d_{out}}{e}^{z_j}}$$
     Softmax 函数不仅可以将输出值映射到[0,1]区间，还满足所有的输出值之和为 1 的特性。但是在 Softmax 函数的数值计算过程中，容易因输入值偏大发生数值溢出现象；在计算交叉熵时，也会出现数值溢出的问题。TensorFlow 中提供了一个统一的接口，将 Softmax 与交叉熵损失函数同时实现，函数式接口为tf.keras.losses.categorical_crossentropy(y_true,y_pred,from_logits=False)，其中 y_true 代表了one-hot 编码后的真实标签，y_pred 表示网络的预测值，from_logits 为 True 时，y_pred 表示须为未经过 Softmax 函数的变量 z；当from_logits 为 False 时，y_pred 表示为经过 Softmax 函数的输出。类方式为losses.CategoricalCrossentropy(from_logits)同时实现 Softmax 与交叉熵损失函数的计算。

   • ∈ [−1,  1] 输出值在[-1, 1]之间。

6. 损失函数及误差计算

   • 均方差

     均方差误差(Mean Squared Error, MSE)函数把输出向量和真实向量映射到笛卡尔坐标系的两个点上，通过计算这两个点之间的欧式距离(准确地说是欧式距离的平方)来衡量两个向量之间的差距：
     $$MSE:=\frac{1}{d_{out}}\sum _{i=1}^{d_{out}}(y_i-o_i{)}^2$$
     可以通过函数的方式实现：

     loss = keras.losses.MSE(y_pred, y_true)
     

     也可以通过层方式实现：

     criteon = keras.losses.MeanSquaredError()
     loss = criteon(y_pred, y_true)
     

   • 交叉熵及KL散度

     熵在信息学科中也叫信息熵，或者香农熵。熵越大，代表不确定性越大，信息量也就越大。某个分布 P()的熵定义为：
     $$H(P):=-\sum _{i}P(i)lo{g}_{2}P(i)$$
     在 TensorFlow 中间，我们可以利用 tf.math.log 来组合计算熵。基于熵引出交叉熵(Cross Entropy)的定义:
     $$H(p,q):=-\sum _{i=0}p(i)lo{g}_2[q(i)]$$
     交叉熵可以分解为 p 的熵()与 p,q 的 KL 散度(Kullback-Leibler Divergence)的和：
     $$H(p,q):=H(p)+D_{KL}(p|q)$$
     其中KL散度定义为：
     $$D_{KL}(p|q)=\sum _{x\in X}p(x)log(\frac{p(x)}{q(x)})$$
     需要注意的是，交叉熵和KL散度都是不对称的，即：
     $$\begin{gathered} H(p,q)\ne H(q,p) \\ {D}_{KL}(p|q)\ne D_{KL}(q|p) \end{gathered}$$
     特别地，当分类问题中 y 的编码分布采用one-hot 编码时：() = 0，此时：
     $$H(y,o)=H(y)+D_{KL}(y|o)=D_{KL}(y|o)=\sum _j{y}_{i}log(\frac{y_j}{o_j})$$
     即：
     $$H(y,o)=1\ast log\frac{1}{o_i}+\sum _{j\ne i}0\ast log(\frac{0}{o_j})=-log{o}_i$$
     其中为 One-hot 编码中为 1 的索引号。最小化交叉熵的过程也是最大化正确类别的预测概率的过程。从这个角度去理解交叉熵损失函数，非常直观易懂。

   • 损失函数可以自定义。

7. 反向传播

   我们把函数所有偏导数写成向量形式：
   $$\nabla L=(\frac{\delta L}{\delta {\theta }_1},\frac{\delta L}{\delta {\theta }_2},...,\frac{\delta L}{\delta {\theta }_n})$$
   此时梯度下降算法可以按着向量形式进行更新：
   $${\theta }^{{}^{\prime }}=\theta -\eta \nabla L$$
   梯度下降算法一般是寻找函数的最小值，有时希望求解函数的最大值，如增强学习中希望最大化奖励函数，则可按着梯度方向更新:
   $${\theta }^{{}^{\prime }}=\theta +\eta \nabla L$$
   这样，则可以从通过某损失函数的输出层开始，求取每个节点对应的所有超参数的偏导数，通过上式，更新对应的超参数；然后向后传播，依次求取倒数第一层隐藏层、倒数第二层隐藏层至更新输入层与第一层隐藏层的超参数为止。此时整个网络的参数已经得到更新，再次进行下一轮的前向传播，如此重复，直到损失函数、准确率等评判标准满足要求为止。

   求导数的时候如果输出值经过某个激活函数，则需要利用链式求导规则，对复合后的函数进行求导，然后再进行上述计算。

   根据此原理，则可以手动推到偏导计算式，再利用编程实现相应的求导公式，利用相应的输出进行超参数更新。在Tensorflow 2.0中，提供了自动求导工具，即通过梯度记录器进行函数梯度的计算，如下：

   with tf.GradientTape() as tape: # 梯度记录器,定义别名tape
       x = tf.random.normal([4,28*28])
       out = model(x)
       loss = any_loss_function()
   grad = tape.gradient(loss, model.trainable_variables)
   optimizer.apply_gradients(zip(grads, model.trainable_variables))
   

   上述代码中，将整个前向传播过程的计算式或者层写到函数梯度记录器的with结构中，再把整个训练过程的损失函数最后一个函数以及需要求偏导的参数传递到梯度记录器的gradient方法中，以此求取全局中各个节点所对应的超参数的梯度，最后再用此梯度求取更新后的超参数。

8. 测量工具

   在网络的训练过程中，经常需要统计准确率，召回率等信息，除了可以通过手动计算并平均方式获取统计数据外，keras 提供了一些常用的测量工具 keras.metrics，专门用于统计训练过程中需要的指标数据。

   • 新建测量器：loss_meter = metrics.Mean()(还有其他的统计测量器)
   • 写入数据：loss_meter.update_state(float(loss)), 也可以直接将梯度记录器中的损失函数等需要测量的输出函数对象传入测量工具对象。（真实值在前，预测值在后）。
   • 读取统计信息：loss_meter.result()
   • 清除：loss_meter.reset_states()，一般每次读取完测量结果后，清零统计信息，以便下一轮统计的开始。

9. 可视化

   TensorFlow 提供了一个专门的可视化工具，叫做TensorBoard，他通过 TensorFlow 将监控数据写入到文件系统，并利用 Web 后端监控对应的文件目录，从而可以允许用户从远程查看网络的监控数据。其创建过程如下：

   • 模型端

     在模型端，需要创建写入监控数据的 Summary 类，并在需要的时候写入监控数据。首先通过 tf.summary.create_file_writer 创建监控对象，并制定监控数据的写入目录：

     summary_writer = tf.summary.create_file_writer(log_dir)
     

     在前向计算完成后，对于误差这种标量数据，我们通过 tf.summary.scalar 函数记录监控数据，并指定时间戳 step:

     with summary_writer.as_default(): 
      	# 当前时间戳 step 上的数据为 loss，写入到 ID 位 train-loss 对象中
      	tf.summary.scalar('train-loss', float(loss), step=step)
     

     需要注意的是，TensorBoard 通过字符串 ID 来区分不同类别的监控数据，因此对于误差数据，我们将它命名为”train-loss”，其他类的数据不可写入此对象，防止数据污染。

     对于图片类型的数据，通过 tf.summary.image 函数写入监控图片数据：

     with summary_writer.as_default():
      	# 写入测试准确率
      	tf.summary.scalar('test-acc', float(total_correct/total),step=step)
      	# 可视化测试用的图片，设置最多可视化 9 张图片
      	tf.summary.image("val-onebyone-images:", val_images, max_outputs=9, step=step)
     

     除了监控标量数据和图片数据外，TensorBoard 还支持通过 tf.summary.histogram 查看张量的数据直方图分布，以及通过 tf.summary.text 打印文本信息：

     with summary_writer.as_default(): 
      	# 当前时间戳 step 上的数据为 loss，写入到 ID 位 train-loss 对象中
      	tf.summary.scalar('train-loss', float(loss), step=step) 
      	# 可视化真实标签的直方图分布
      	tf.summary.histogram('y-hist',y, step=step)
      	# 查看文本信息
      	tf.summary.text('loss-text',str(float(loss)))
     

     运行模型程序后，相应的数据将写入到指定文件目录中。

   • 浏览器端

     在运行程序时，通过运行 tensorboard --logdir path 指定 Web 后端监控的文件目录
     path，如图：

   

   此时打开浏览器，并输入网址 http://localhost:6006 (也可以通过 IP 地址远程访问，具体端口号可能会变动，可查看命令提示) 即可监控网络训练进度。

10. 神经网络的优化

    机器学习的主要目的是从训练集上学习到数据的真实模型，从而能够在未见过的测试集上面也能够表现良好，我们把这种能力叫做泛化能力。

    模型的容量或表达能力，是指模型拟合复杂函数的能力。一种体现模型容量的指标为模型的假设空间(Hypothesis Space)大小，即模型可以表示的函数集的大小。假设空间越大越完备，从假设空间中搜索出逼近真实模型的函数也就越可能；反之，如果假设空间非常受限，就很难从中找到逼近真实模型的函数。

    为了挑选模型超参数和检测过拟合、欠拟合现象，一般需要将原来的训练集再次切分为新的训练集和验证集(Validation set)，即数据集需要切分为训练集、验证集和测试集 3 个子集。一般训练集用于训练得到模型超参数；验证集用于得出评判模型好坏的相关信息，用于选择合适的模型超参数，即根据验证集的性能表现调整学习率、权值衰减系数、训练次数、网络结构以及是否出现过拟合或者欠拟合；而测试集则用于检测模型的泛化能力，则测试集的性能不能作为模型训练的反馈。为了防止训练的模型记住数据的特征，测试集不应该参与模型训练。

    过拟合与欠拟合：

    • 过拟合

      在训练集上面表现较好，但是在未见的样本上表现不佳，也就是泛化能力偏弱，我们把这种现象叫做过拟合(Overfitting)。当设置模型的假设空间过大时，我们发现学到的模型很有可能过分去拟合训练样本，导致学习模型在训练样本上的误差非常小，甚至比真实模型在训练集上的误差还要小。但是对于测试样本，模型性能急剧下降，泛化能力非常差。

    • 欠拟合

      模型不能够很好的学习到训练集数据的模态，导致训练集上表现不佳，同时在未见的样本上表现也不佳，我们把这种现象叫做欠拟合(Underfitting)。如果我们用模型容量小于真实模型的线性函数去回归这些数据，会发现很难找到一条线性函数较好地逼近训练集数据的模态，具体表现为学习到的线性模型在训练集上的误差(如均方差)较大，同时在测试集上面的误差也较大。

    通过观测训练准确率和验证准确率可以大致推断模型是否过拟合和欠拟合。如果模型的训练误差较低，训练准确率较高，但是验证误差较高，验证准确率较低，那么可能出现了过拟合现象。如果训练集和验证集上面的误差都较高，准确率较低，那么可能出现了欠拟合现象。

    • 解决办法：

      • 当我们发现当前的模型在训练集上面误差一直维持较高的状态，很难优化减少，同时在测试集上也表现不佳时，我们可以考虑是否出现了欠拟合的现象，这个时候可以通过增加神经网络的层数、增大中间维度的大小、尝试更复杂的网络结构等手段，比较好的解决欠拟合的问题。

      • 当观测到过拟合现象时，可以重新设计网络模型的容量，如降低网络的层数、降低网络的参数量、添加假设空间的约束等，使得模型的容量降低，从而减轻或去除过拟合现象。

      • 数据增强

        数据增强(Data Augmentation)是指在维持样本标签不变的条件下，根据先验知识改变样本的特征，使得新产生的样本也符合或者近似符合数据的真实分布。以图片数据为例，对于图片，根据先验知识，旋转、缩放、平移、裁剪、改变视角、遮挡某局部区域都不会改变图片的类别标签，因此可以采用相关操作实现数据增强：

        x = tf.image.rot90(x,k=1) #旋转k个90°
        x = tf.image.random_flip_left_right(x) #随机水平翻转
        x = tf.image.random_flip_up_down(x) # 随机竖直翻转
        x = tf.image.resize(x, [244, 244]) # 缩放
        x = tf.image.random_crop(x, [224,224,3]) #随机裁剪
        

        通过生成模型在原有数据上学习到数据的分布，从而生成新的样本，这种方式也可以在一定程度上提升网络性能。如通过自编码器、条件生成对抗网络(Conditional GAN, CGAN)可以生成带标签的样本数据。

      对于神经网络，即使网络结构超参数保持不变(即网络最大容量固定)，模型依然会出现过拟合的现象，这是因为神经网络的有效容量和网络参数的状态息息相关，神经网络的有效容量可以很大，也可以通过稀疏化参数、添加正则化等手段降低。

      • 正则化：

        通过设计不同层数、大小的网络模型可以为优化算法提供初始的函数假设空间，但是模型的实际容量可以随着网络参数的优化更新而产生变化。

        此时，通过限制网络参数的稀疏性，可以来约束网络的实际容量。这种约束一般通过在损失函数上添加额外的参数稀疏性惩罚项实现，在未加约束之前的优化目标是：
        $$MinimizeL(f_{\theta }(x),y),(x,y)\in D^{train}$$
        对模型的参数添加额外的约束后，优化的目标变为:
        $$MinimizerL(f_{\theta }(x),y)+\lambda \Omega (\theta ),(x,y)\in D^{train}$$
        其中，$\Omega (\theta )$表示对超参数$\theta$的稀疏性约束函数，一般通过超参数的L范数实现。可以是L0，L1,L2范数，其中L0范数不可导，所以不适用于梯度下降算法优化。

        正则化施加到全局同类参数。可以在定义网络层的时候，设置

      • Dropout：

        Dropout 通过随机断开神经网络的连接，减少每次训练时实际参与计算的模型的参数量；但是在测试时，Dropout 会恢复所有的连接，保证模型测试时获得最好的性能。在添加了 Dropout 功能的网络层中，每条连接是否断开符合某种预设的概率分布，如断开概率为的伯努利分布。

        可以通过 tf.nn.dropout(x, rate)函数实现某条连接的 Dropout 功能，其中 rate 参数设置断开的概率值：

        x = tf.nn.dropout(x, rate=0.5)
        

        也可以将 Dropout 作为一个网络层使用，在网络中间插入一个 Dropout 层：

        model.add(layers.Dropout(rate=0.5))
        

    神经网络建模之后，模型可能在现有的验证集，测试集均有良好的性能，然而不能更好的贴合实际使用。例如，商店进货，当利润明显高于成本的时候，期望预测进货量能稍多于市场需求，但是当利润比较低的时候，期望预测的进货量能稍低于市场需求，以此使得亏本的风险尽可能降低。此时，常用的现有损失函数很可能便不适用于当前模型的训练。遇到这样的情况，可以根据实际情况定义损失函数，以此使得相关收益最大化，从而训练得到更加贴合实际的模型。

    有时我们在训练网络的时候，可能会发现模型性能判断的标准，如损失函数值、验证集准确率等，在一个比较大的范围类波动，因而难以收敛；或是能够收敛，但是收敛速度比较慢，甚至训练结束之后，若在此模型的基础上继续进行训练，损失函数值还会继续降低、验证集准确率还会继续升高的情况。此时可以考虑学习率的设置不合适。学习率过大，会出现振荡不收敛的情况，过小则会出现收敛过慢的情况。为了使得学习率能够很好的贴合模型训练的需要，可以考虑使用指数衰减学习率，使得开始时的学习率较大，收敛相对较快，而随着训练的进行，学习率不断减少，使得训练结果能够收敛。指数衰减学习率的计算公式如下：
    $$learning\_rate=base\_rate\ast decay\_rate\ast \frac{gloable\_step}{batch\_size}$$
    其中，base_rate，为基础学习率，decay_rate，为学习率衰减率，gloable_step为当前训练轮数，批量训练的样本数。一般将学习率的更新频率设置为总的样本数除以批量训练的样本数。目前指数衰减学习率API在2.0中被移除，如有需要，可以考虑自行实现。或者实现其他具有类似效果的函数，以实现学习率的动态变化。

11. 模型的保存与加载

    模型训练完成后，需要将模型保存到文件系统上，从而方便后续的模型测试与部署工作。在训练时间隔性地保存模型状态也是非常好的习惯，这一点对于训练大规模的网络尤其重要，一般大规模的网络需要训练数天乃至数周的时长，一旦训练过程被中断或者发生宕机等意外，之前训练的进度将全部丢失。

    • 张量方式

      网络的状态主要体现在网络的结构以及网络层内部张量参数上，因此在拥有网络结构源文件的条件下，直接保存网络张量参数到文件上是最轻量级的一种方式。通过调用Model.save_weights(path)方法即可讲当前的网络参数保存到 path 文件上：

      network.save_weights('weights.ckpt')
      

      上述代码将 network 模型保存到 weights.ckpt 文件上，在需要的时候，只需要先创建好网络对象，然后调用网络对象的 load_weights(path)方法即可将指定的模型文件中保存的张量数值写入到当前网络参数中去：

      # 保存模型参数到文件上
      network.save_weights('weights.ckpt')
      print('saved weights.')
      del network # 删除网络对象
      # 重新创建相同的网络结构
      network = Sequential([layers.Dense(256, activation='relu'),
       	layers.Dense(128, activation='relu'),
       	layers.Dense(64, activation='relu'),
       	layers.Dense(32, activation='relu'),
       	layers.Dense(10)])
      # 配置网络
      network.compile(optimizer=optimizers.Adam(lr=0.01),
      loss=tf.losses.CategoricalCrossentropy(from_logits=True),
      metrics=['accuracy']) 
      # 从参数文件中读取数据并写入当前网络
      network.load_weights('weights.ckpt')
      print('loaded weights!')
      

      从上述代码可以看出，需要加载模型的时候，需要记住网络结构，并复现网络结构之后，再通过模型的load_weights方法加载模型。

    • 网络方式

      通过 Model.save(path)函数可以将模型的结构以及模型的参数保存到一个 path 文件上，在不需要网络源文件的条件下，通过 keras.models.load_model(path)即可恢复网络结构和网络参数。如：

      # 保存模型结构与模型参数到文件
      network.save('model.h5')
      print('saved total model.')
      del network # 删除网络对象
      # 从文件恢复网络结构与网络参数
      network = tf.keras.models.load_model('model.h5')
      

    • SavedModel 方式

      通过 tf.keras.experimental.export_saved_model(network, path)即可将模型以SavedModel方式保存到 path 目录中，此方法更具有平台无关性。如：

      # 保存模型结构与模型参数到文件
      tf.keras.experimental.export_saved_model(network, 'model-savedmodel')
      print('export saved model.')
      del network # 删除网络对象
      # 从文件恢复网络结构与网络参数
      network=tf.keras.experimental.load_from_saved_model('model-savedmodel')
      

12. 自定义网络层及模型容器类

    一般直接使用层方式来完成模型的搭建，在 tf.keras.layers 命名空间(后续使用 layers 指代 tf.keras.layers)中提供了大量常见网络层的类接口，如全连接层，激活含水层，池化层，卷积层，循环神经网络层等。同时在tf.keras命名空间下，定义了Sequential()容器类，进行网络层结构的封装，以此得到模型对象。而Sequential()类中提供了add()方法，可以动态的将网络层结构加入到模型容器中，以此实现神经网络的动态创建。如：

    network = Sequential([layers.Dense(256, activation='relu'),
     	layers.Dense(128, activation='relu'),
     	layers.Dense(64, activation='relu'),
     	layers.Dense(32, activation='relu'),
     	layers.Dense(10)])
    
    network.add(layers.Dense(5)) # 继续添加神经网络层
    

    除了本身包含的网络层及模型容器外，用户还可以方面的自定义相应的网络层及网络模型。

    • 自定义网络层

      对于自定义的网络层，需要实现初始化__init__方法和前向传播逻辑 call方法。我们以某个具体的自定义网络层为例，假设我们需要一个没有偏置的全连接层，即 bias 为 0，同时固定激活函数为 ReLU 函数。如：

      class MyDense(layers.Layer):
      	# 自定义网络层
      	def __init__(self, inp_dim, outp_dim):
      		super(MyDense, self).__init__()
      		# 创建权值张量并添加到类管理列表中，设置为需要优化,也可以设置为不可训练变量
      		self.kernel = self.add_variable('w',[inp_dim,outp_dim],trainable=True)
      
      	def call(self, inputs, training=None):
      		# 实现自定义类的前向计算逻辑
      		# X@W
      		out = inputs @ self.kernel # 矩阵运算，也可以为out=tf.matmul(inputs,self.kernel)
      		# 执行激活函数运算
      		out = tf.nn.relu(out)
      		return out
      

      自定义类的前向运算逻辑需要实现在 call(inputs, training)函数中，其中 inputs 代表输入，由用户在调用时传入；training 参数用于指定模型的状态：training 为 True 时执行训练模式，training 为 False 时执行测试模式，默认参数为 None，即测试模式。由于全连接层的训练模式和测试模式逻辑一致，此处不需要额外处理。对于部份测试模式和训练模式不一致的网络层，需要根据 training 参数来设计需要执行的逻辑。

    • 自定义网络模型

      我们可以继承基类来实现任意逻辑的自定义网络类。下面我们来创建自定义网络容器类，首先创建并继承 Model 基类，分布创建对应的网络层对象：

      class MyModel(keras.Model):
          # 自定义网络类，继承自 Model 基类
      	def __init__(self):
      		super(MyModel, self).__init__()
      		# 完成网络内需要的网络层的创建工作
      		self.fc1 = MyDense(28*28, 256)
      		self.fc2 = MyDense(256, 128)
      		self.fc3 = MyDense(128, 64)
      		self.fc4 = MyDense(64, 32)
      		self.fc5 = MyDense(32, 10)
              
              #网络模型前向传播定义
          def call(self, inputs, training=None):
      		# 自定义前向运算逻辑
      		x = self.fc1(inputs) 
      		x = self.fc2(x) 
      		x = self.fc3(x) 
      		x = self.fc4(x) 
      		x = self.fc5(x) 
      		return x
      

      最后可以通过实例化自定义的模型类进行神经网络的计算。

13. 神经网络MNIST手写字识别实战

    源代码：

    import tensorflow as tf
    from tensorflow import keras
    from tensorflow.keras import layers, optimizers, Sequential, losses, datasets
    
    
    BATCH_SIZE = 64
    EPOCH_SIZE = 5
    PRINT_TEMPLATE = "train_loss: {:.4f}, train_accuracy: {:.4f}, test_loss: {:.4f}, test_accuracy: {:.4f}"
    
    # import data
    (x_train, y_train), (x_test, y_test) = datasets.mnist.load_data()
    x_train, x_test = x_train / 255.0, x_test/255.0
    data_train = tf.data.Dataset.from_tensor_slices((x_train, y_train))
    data_test = tf.data.Dataset.from_tensor_slices((x_test, y_test))
    data_train = data_train.shuffle(10000).batch(BATCH_SIZE)
    data_test = data_test.shuffle(5000).batch(BATCH_SIZE)
    
    # def layers and model
    model = Sequential([
        layers.Flatten(input_shape=(28, 28)),
        layers.Dense(784),
        layers.Dense(500),
        layers.Dense(10)])
    
    # def optimizer and loss
    criteon = losses.CategoricalCrossentropy(from_logits=True)
    optimizer = optimizers.Adam()
    
    # def metrics
    train_loss_metric = keras.metrics.Mean(name='train_loss_metric')
    train_acc_metric = keras.metrics.SparseCategoricalAccuracy(name='train_acc_metric')
    test_loss_metric = keras.metrics.Mean(name='test_loss_metric')
    test_acc_metric = keras.metrics.SparseCategoricalAccuracy(name='test_acc_metric')
    
    # train the model
    for epoch in range(EPOCH_SIZE):
        # reset the metrics state
        train_loss_metric.reset_states()
        train_acc_metric.reset_states()
        test_loss_metric.reset_states()
        test_acc_metric.reset_states()
        # training
        for step, (x, y) in enumerate(data_train):
            with tf.GradientTape() as tape:
                pred = model(x)
                y_onehot_train = tf.one_hot(y,depth=10)
                loss = criteon(y_onehot_train, pred)
            grads = tape.gradient(loss, model.trainable_variables)
            optimizer.apply_gradients(zip(grads, model.trainable_variables))
            train_loss_metric(loss)
            train_acc_metric(y, pred) # 注：y_true在前，y_pred在后
    
        # test the model
        for step_t, (x_t, y_t) in enumerate(data_test):
            y_onehot_t = tf.one_hot(y_t,depth=10)
            pred_t = model(x_t)
            loss_t = criteon(y_onehot_t, pred_t)
            test_loss_metric(loss_t)
            test_acc_metric(y_t, pred_t)
    
        print(PRINT_TEMPLATE.format(train_loss_metric.result(),train_acc_metric.result(),
                                    test_loss_metric.result(),test_acc_metric.result()))
    

    结果：

    train_loss: 0.4071, train_accuracy: 0.8842, test_loss: 0.3420, test_accuracy: 0.9014
    train_loss: 0.3371, train_accuracy: 0.9042, test_loss: 0.3206, test_accuracy: 0.9104
    train_loss: 0.3268, train_accuracy: 0.9082, test_loss: 0.3200, test_accuracy: 0.9120
    train_loss: 0.3132, train_accuracy: 0.9117, test_loss: 0.3285, test_accuracy: 0.9086
    train_loss: 0.3020, train_accuracy: 0.9148, test_loss: 0.2983, test_accuracy: 0.9174
    

    随便定义的无优化措施网络，结果并不理想。