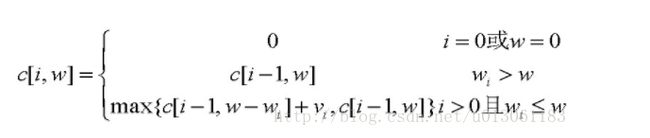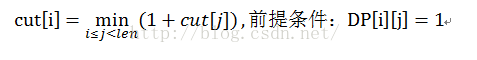LeetCode(132)分割回文串 II和背包问题
一.01背包问题
一、问题描述:有n 个物品,它们有各自的重量和价值,现有给定容量的背包,如何让背包里装入的物品具有最大的价值总和?
二、总体思路:根据动态规划解题步骤(问题抽象化、建立模型、寻找约束条件、判断是否满足最优性原理、找大问题与小问题的递推关系式、填表、寻找解组成)找出01背包问题的最优解以及解组成,然后编写代码实现;
三,原理:当前物品重量wi大于当前背包容量w的时候,直接去前一个物品在背包容量为w时的最大价值,否则取前一个物品在w时的最大价值 和 前一个物品在w-wi的最大价值加上当前物品vi的价值 中最大的价值。
def bag(n, c, w, v) -> "n 是个数,c是背包最大容量,w是物品的的重量,v是物品的价值":
w.insert(0, 0)
v.insert(0, 0) # 为了是序号跟res保持同步,因为res是从1开始计算的
res = [[-1 for i in range(c + 1)] for j in range(n + 1)]
for j in range(c + 1):
res[0][j] = 0
for i in range(1, n + 1):
for j in range(1, c + 1):
if j < w[i]:
res[i][j] = res[i - 1][j]
else:
res[i][j] = max((res[i - 1][j], res[i - 1][j - w[i]] + v[i]))
print(res[1:])
return res
def show(n, c, w, res):
print('最大价值为:', res[n][c])
x = [False for i in range(n)]
j = c
for i in range(n, 0, -1):
if res[i][j] > res[i - 1][j]:
x[i - 1] = True
j -= w[i - 1]
print('选择的物品为:')
for i in range(n):
if x[i]:
print('第', i, '个,')
print('')
if __name__ == '__main__':
n = 5
c = 10
w = [2, 2, 6, 5, 4]
v = [6, 3, 5, 4, 6]
res = bag(n, c, w, v)
show(n, c, w, res)
然后我们想改进解法:你会发现,res[i][j],只跟res[i-1][j]和res[i-1][j-w[i]]有关,即j只跟i1层的小于等于那么j的值有关,如果每一行j从最后更新,那么一维数组就能保存所有的信息。
def bag(n, c, w, v) -> "n 是个数,c是背包最大容量,w是物品的的重量,v是物品的价值":
w.insert(0, 0)
v.insert(0, 0) # 为了是序号跟res保持同步,因为res是从1开始计算的
res = [0 for j in range(c+1)]
for i in range(1, n + 1):
for j in range(c, 0, -1): # j从大到小循环,这样可以使一维数组保存所有信息。
if j二.分割回文串 II
重述题意:输入一个字符串,将其进行分割,分割后各个子串必须是“回文”结构,要求最少的分割次数。显然,为了求取最少分割次数,一个简单的思路是穷尽所有分割情况,再从中找出分割后可构成回文子串且次数最少的分割方法。
解题思路:对于输入字符串如s=“aab”,一个直观的思路是判断“aab”是否构成回文,根据回文的特点是对称性,那么,我们可以判断s[0]与s[2]是否相等,不等,因此“aab”不能构成回文,此后再怎么判断呢???这种无章法的操作没有意义,因为一个字符串构成回文的情况是很复杂的,对于一个长度为n的字符串,其构成回文的子串长度可能的长度分布范围可以是1—n:整体构成回文如“baab”,则子串长度可为n=4;如“cab”,只能构成长度为1的回文子串。
鉴于上述分析,对于一个字符串,我们需要考虑所有可能的分割,这个问题可以抽象成一个DP问题,对于一个长度为n的字符串,设DP[i][j]表示第i个字符到第j个字符是否构成回文,若是,则DP[i][j]=1;若否,则DP[i][j]=0;如此,根据回文的约束条件(对称性),DP[i][j]构成回文需满足:
1、输入字符串s[i]==s[j],对称性;
2、条件1满足并不能保证i到j构成回文,还须:(j-i)<=1或者DP[i+1][j-1]=1;即,i、j相邻或者i=j,也就是相邻字符相等构成回文或者字符自身构成回文,如果i、j不相邻或者相等,i到j构成回文的前提就是DP[i+1][j-1]=1.
所以状态转移方程:DP[i][j]=(s[i]==s[j]&&(j-i<=1||DP[i+1][j-1]==1))。
由于i必须小于j,i>=0&&i
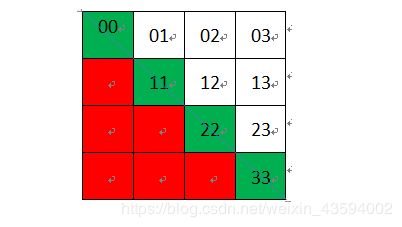
经过判断,得到状态矩阵:绿色部分,即字符串“baab”可构成的回文子串分割情况:绿色部分DP[0][0]、DP[1][1]、DP[2][2]和DP[3][3]构成的是单字符回文子串,DP[1][2]和DP[0][3]构成的是多字符回文子串。
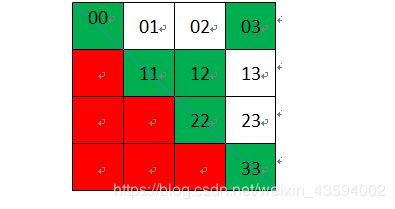
在得到输入字符串的所有回文子串的分割情况之后,我们需要考虑如何求取回文子串的最小分割次数,显然,回文子串越长,分割次数越少,因此,分割的时候回文子串应分别取最大长度,如上面的例子,s=“baab”,可行的分割情况有三种:(显然,最少分割次数为0,当然,根据DP[][]矩阵可以很容易求取最长回文子串!
1、{DP[0][0]、DP[1][1]、DP[2][2]、DP[3][3]};
2、{DP[0][0]、DP[1][2]、DP[3][3]};
3、{DP[0][3]}
当输入字符串所有可能的分割情况求出来之后,我们需要进一步寻找最少分割次数,我们可以用一个一维数组来存储分割次数:设int[] cut=new int[s.length()+1],cut[i]表示第i个字符到最后一个字符所构成的子串的最小分割次数,这里的i有约束条件,就是第i个位置必须是可进行回文分割的,即DP[i][j]==1 (j>=i&&j 根据这个公式,我们最终要求的cut[0]与cut[0]、cut[1]…cut[len]都有关,直接求需要递归,效率低,因此我们可以逆序求解,即:先求cut[len-1],最后求cut[0].class Solution(object):
def minCut(self, s):
"""
:type s: str
:rtype: int
"""
s = '$' + s
dp = [sys.maxint for i in range(len(s)+1)]
dp[1] = 0
for i in range(2,len(s)+1):
if s[1:i+1] == s[1:i+1][::-1]:
dp[i] = 0
else:
for j in range(2,i+1):
if s[j:i+1] == s[j:i+1][::-1]:
dp[i] = min(dp[i],dp[j-1] + 1)
return dp[len(s)]