一个二维码能装10T电影?看样子我都能改变世界了。
![]()
大意是中国专利局公开了一项申请,有家公司发明了一个非常牛逼的压缩算法,理论上能做到 万亿分之一的压缩比例。

按照他的说法 10T 大小的内容我们也可以轻松压缩到 6000比特,换算下来只有0.73 KB ,还不及一张表情包的大小。
这是啥水平?用这算法压缩以后,上百部电影也只要一眨眼就能下载完。
而现在的二维码技术可以做到单张二维码存储接近3000字节的信息,也就是说, 只要一个小小的二维码,就可以带走数量庞大的电影,你说听起来牛不牛逼??

这要是真的,对人类意义可是巨大。
众所周知,计算机数据会占用存储空间。为了节约空间,人们研究出了压缩技术,分为 「有损压缩」和「无损压缩」两个领域。
其中有损压缩指的就是像MP3、JPG一样的文件,日常生活中我们用不着听特别高清的音乐,看特别高清的图片,因此 会主动消除掉一些数据来减少空间。

这类压缩有个特点,就是我们得到的结果最多就是看个糊一点的图片,不至于不能用。
这个方法的核心思路,就是用更少的信息「替换」表达原来的信息,打个比方,我们在和朋友描述电话号码时「 1111 」转而用「 4 个 1 」代替,这个过程少说了 1 个字,这也算是某种压缩。
无损压缩的过程有点像「翻字典」。

大家都知道英文单词比较长,中文同意词汇比较短,文言文则更短。。。一个好的压缩算法就好比将几十个字母的英文句子翻译为十个字的文言文。
我们举一个例子,比如我们需要压缩这样一串字符: 「abcabcaacabdaacabd」。
但是在仔细观察后,可以发现在字符串中存在着多个重复的字符串 「abc」, 「aac」以及 「abd」。

那么只要我们建立一个对照翻译表, 用「 1 」代替字符串「 abc 」,用数字「 2 」代替字符串「 aac 」,用数字「 3 」代替字符串「 abd 」。
整个字符串可以简化为了 「 112323 」的数字串,相较于原始字符串已经精简了许多。
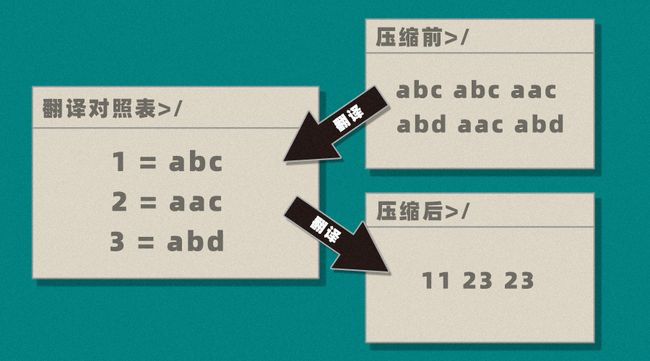
如果更进一步,用「Ⅰ」代表「11」,用「Ⅱ」代表「23」,这样字符串还可以精简为 「 Ⅰ Ⅱ Ⅱ 」。

电脑里的压缩文件过程原理大概就是如此,只不过实际上文件不是只有字符串,而且数据量比这个大得多。
解压缩的原理自然也很容易想到,回到前面的例子中,我们只需要对照翻译表将数字重新还原,就能够得到原始字符串。

这样一套操作逻辑就叫做字典编码算法,所谓的翻译对照表也就是算法中的 「字典」,不论是什么压缩算法,都得带着这本「字典」,也就是 解码参数。
不同的压缩方式对应不同的文件格式,我们常见的有 rar/zip/7z 等等,其实就是在告诉电脑这是用什么方式压缩的。
而相应的的翻译工具,则就是常见的压缩软件,相信不少人都被这张图骚扰过↓
理论上来说,我们可以搞一波智障操作,这么写翻译表:abcabcaacabdaacabd = 1 ,整个字符串只用一个数字就能代替了。
但这么干的话,字典本身的大小就和原文一样了,再加上压缩后的数字, 信息量反倒变大了。
所以说这事儿挺不简单的,目前为止工程师们研究出了很多方法,最快的压缩效率也只是接近 2 : 1 。

所以才说开头那个万亿分之一的消息惊得让我摔在了地上。
事实上,工程师怎么实现是一回事,压缩的极限比例其实能用数学工具算出来。
这就不得不提到一位天降猛男,信息论之父—— 克劳德·香农。

作为一个伟大的科学家,克劳德·香农提出了信息熵函数,而在后续学者的配合下,终结了这个疑问。
信息熵公式▼
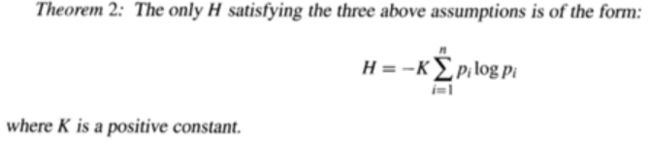
总而言之, 在这个宇宙里,信息压缩的比例是存在理论上限的,和信息的复杂程度有关,但是远远达不到万亿分之一,这个专利要真能达到万亿分之一,香农的棺材板都要压不住了。。。

果然,在文章并没有与万亿级相关的字眼和描述,取而代之的则是千分之一和万分之一的描述。

也不是,尽管在文章中没有提到万亿级压缩,但是申请者对自己的专利也是信心满满: 理论上任何数据都可以压缩到只剩 2 个比特和解码参数。

还记得前面提到的智障操作吗?。。。压缩到 2 个比特情况下没提解码参数有多大,这不耍流氓么?
而且就算不谈万亿级别的压缩率,仅仅是万分之一的压缩率可以实现吗?
可以, 很简单,但没有任何意义:
假设我有个由 100万个 a 组成的字符串,那我就只需要用「 100万个 a 」这句话,就完成了这波极限操作。
还记得差评君以前介绍过的 压缩炸弹吗?一个 42 KB 文件通过自我复制 N 遍达到 4.5 PB ,这玩意儿就是压缩比高得吓人,但一点卵用都没。

总之,这个还在申请中的专利绝对不可能有网传万亿分之一的压缩比那么夸张,专利文件里写到的「任何数据都可以压缩到只剩 2 个比特和解码参数」也多半是没有实际意义的极端情况。
话说回来,这玩意儿要真推翻香农的定理或者是打了我的脸,那差评君高兴还来不及呢: 人类的信息科学一直都在解决信息处理和传递问题,要是真那么牛逼,那我们飞出太阳系指日可待。
