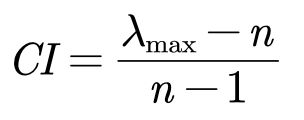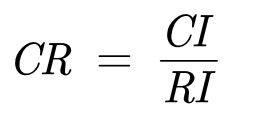数学建模(一)、层次分析法以及代码实现
(刚刚开始学习数学建模,边学习边总结下,慢慢来,当做学习笔记了)
层次分析法
- 什么是层次分析法?
层次分析法可以利用树状的层级结构,将复杂的决策问题在一个层级中区分为数个简单的子问题,并且每个子问题可以独立进行分析,这个层级中的子问题可以包含是任何类型的子问题,无论是有形的还是无形的,仔细计算的或者粗略估计的,理解清晰或模糊的,只要是用于最终决策的子问题都可以包括于此。
一旦这个层级建立完毕,决策专家会有有系统地评估尺度针对每一个部分的相对重要性给予权重数值,其后建立成对比较矩阵,并求出特征向量及特征值,以该特征向量代表每一层级中各部分的优先权,能提供决策者充分的决策资讯并组织有关决策的评选条件或标准(criteria)、权重(weight)和分析(analysis),且能减少决策错误的风险性。
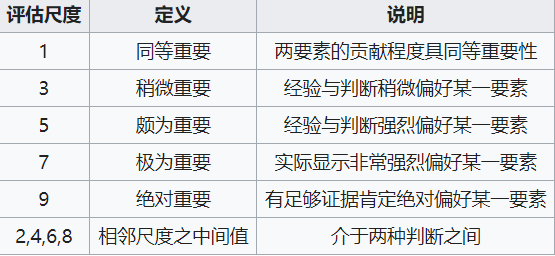
AHP 的评估尺度作为每一层级指标因素间的成对比较,基本划分包括五项,即等强(Equal Strong)、稍强(Weak Strong)、颇强(Strong)、极强(Very Strong)、绝强(Absolution),并赋予名目尺度 1、3、5、7、9 的衡量值,另设四个尺度介于五个基本尺度之间,并赋予 2、4、6、8 的衡量值,共计九个尺度,各尺度所代表之意义如下表所示。
- 如何构建层次分析法
层次分析法的步骤,运用层次分析法构造系统模型时,大体可以分为以下四个步骤:
1.建立层次结构模型;
2.构造判断 (成对比较) 矩阵;
3.层次单排序及其一致性检验;
4.层次总排序及其一致性检验;
- 层次分析法的基本步骤
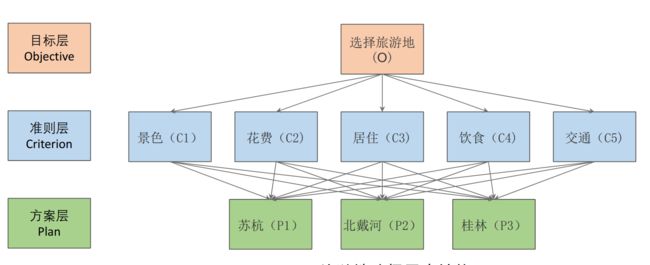
- 建立层次结构模型
将决策的目标、考虑的因素 (决策准则) 和决策对象按他们之间的相互关系分成最高层、中间层和最低层,绘制层次结构图。
最高层 (目标层):决策的目的、要解决的问题;
最低层 (方案层):决策时的备选方案;
中间层 (准则层或指标层):考虑的因素、决策的准则;
如图所示:
2. 构建判断矩阵
对于同一层次的各元素关于上一层次中某一准则的重要性进行两两比较,构造两两比较矩阵(判断矩阵)。
成对比较矩阵是表示本层所有因素针对上一层某一个因素 (准侧或目标) 的相对重要性的比较。
成对比较矩阵的元素aij表示的是第 i个因素相对于第 j个因素的比较结果,这个值使用的是 Santy 的 1-9 标度方法给出。
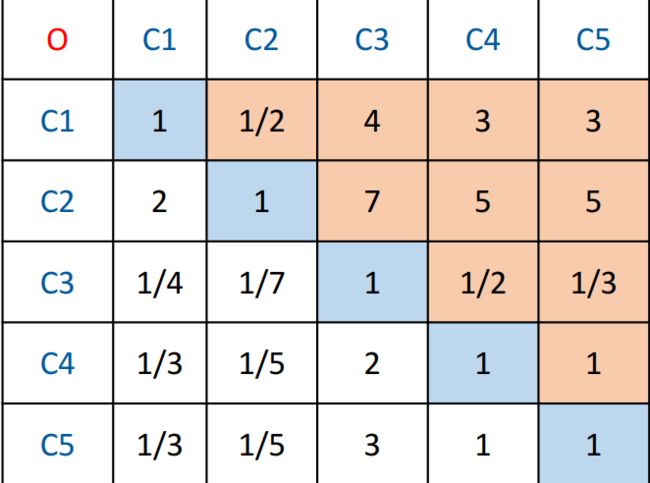
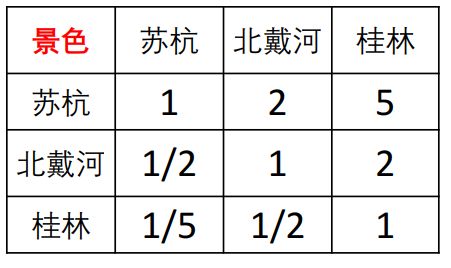
如下图,准则层的判断矩阵O — C
(如上图中2-1,值为2,意为C2比C1略微重要(介于同等重要1和稍微重要3之间吧) )
当我们把所有数据全部比较完,这就是我们的判断矩阵。又因为aij*aji=1,故此也称为正互反矩阵。
上面为目标层到准则层的判断矩阵
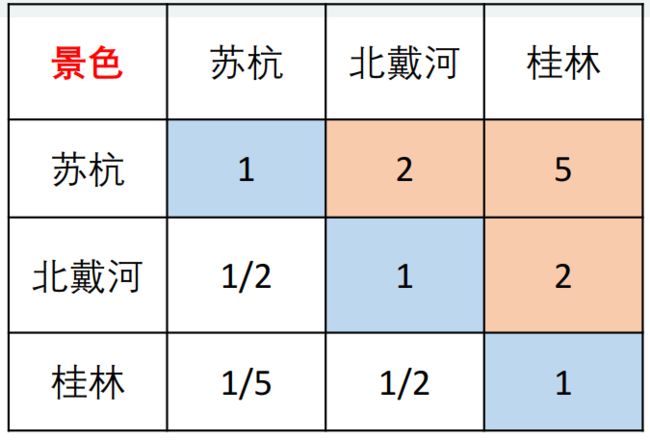
下面则需要继续仿照上面写出准则层到方案层的判断矩阵
上图中准则层为景色 方案层为苏杭,北戴河,桂林(需要将所有准则层到方案层全部列出)
3. 层次单排序及一致性检(注意:在使用判断矩阵求权重之前,必须对其进行一致性检验。 )
1. 若矩阵中每个元素 aij>0且满足aij*aji=1,则我们称该矩阵为正互反矩阵。
在层次分析法中,我们构造的判断矩阵均是正互反矩阵。
若正互反矩阵满足 aij*ajk=aik,则我们称为一致矩阵。(各行(列)之间成倍数关系)
2. 一致性检验
(1). 计算一致性指标CI
(2). 查找对应的平均随机一致性指标RI
(3). 计算一致性比例CR
如果CR<0.1,则可认为判断矩阵的一致性可以接收;否则需要对判断矩阵进行修正。
4. 一致矩阵计算权重
方法一、算数平均法求权重
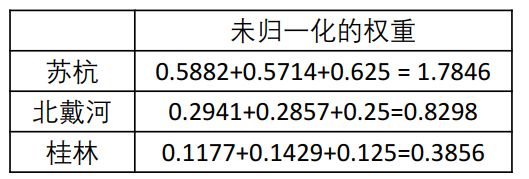
第一步、将判断矩阵按照列归一化(每一个元素除以其所在列的和) (如图)
第二步、将归一化的各列相加(按行求和)
第三步、将相加后得到的向量中每个元素除以n即可得到权重向量
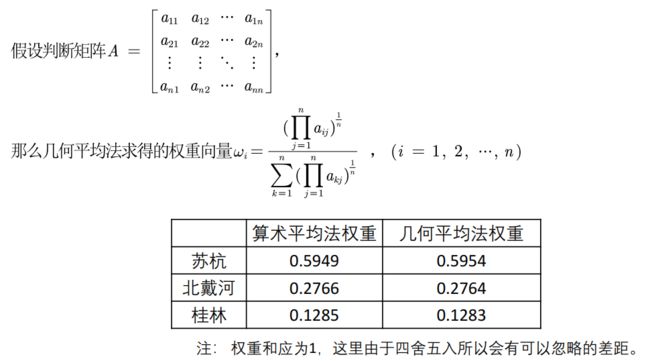
方法二、几何平均法求权重
几何平均法求权重也有三步:
第一步:将A的元素按照行相乘得到一个新的列向量
第二步:将新的向量的每个分量开n次方
第三步:对该列向量进行归一化即可得到权重向量
算法如图:
方法三、特征值法求权重
假如我们的判断矩阵一致性可以接受,那么我们可以仿照一致矩阵权重的求法。
第一步:求出矩阵A的最大特征值以及其对应的特征向量
第二步:对求出的特征向量进行归一化即可得到我们的权重
代码copy的一个网上的,学习学习
disp('请输入判断矩阵A')
A=input('A=');
[n,n] = size(A);
% % % % % % % % % % % % %方法1: 算术平均法求权重% % % % % % % % % % % % %
Sum_A = sum(A);
SUM_A = repmat(Sum_A,n,1);
Stand_A = A ./ SUM_A;
disp('算术平均法求权重的结果为:');
disp(sum(Stand_A,2)./n)
% % % % % % % % % % % % %方法2: 几何平均法求权重% % % % % % % % % % % % %
Prduct_A = prod(A,2);
Prduct_n_A = Prduct_A .^ (1/n);
disp('几何平均法求权重的结果为:');
disp(Prduct_n_A ./ sum(Prduct_n_A))
% % % % % % % % % % % % %方法3: 特征值法求权重% % % % % % % % % % % % %
[V,D] = eig(A);
Max_eig = max(max(D));
[r,c]=find(D == Max_eig , 1);
disp('特征值法求权重的结果为:');
disp( V(:,c) ./ sum(V(:,c)) )
% % % % % % % % % % % % %下面是计算一致性比例CR的环节% % % % % % % % % % % % %
CI = (Max_eig - n) / (n-1);
RI=[0 0.0001 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59]; %这里的RI最多支持 n = 15
% 这里n=2时,一定是一致矩阵,所以CI = 0,我们为了避免分母为0,将这里的第二个元素改为了很接近0的正数
CR=CI/RI(n);
disp('一致性指标CI=');disp(CI);
disp('一致性比例CR=');disp(CR);
if CR<0.10
disp('因为CR<0.10,所以该判断矩阵A的一致性可以接受!');
else
disp('注意:CR >= 0.10,因此该判断矩阵A需要进行修改!');
end
%(关于如何用这个选择女朋友(梦里)
%选一个研究对象… 比如,你的对象… 为了衡量 Ta 的魅力程度,分别从颜值、身高、体重、财富、人文等角度进行评价。分别对上述指标的重要性进行赋权。
%如果暂时没有对象的话,更好… 我们可以选取多个备选方案 (1 号, 2 号… 等等),分别将备选方案的各项指标的实际值与上一步的权重相乘,就得到了每个备选的得分,得分最高的,就是最优方案。
%比如,觉得颜值正义,其他因素不重要,颜值的权重为 0.9,其他因素权重合计为 0.1。 把 1 号, 2 号… N 号拉出来,哪个颜值最好,那他对应的魅力指数就越高…)(手动狗头)