图像降噪算法——小波硬阈值滤波（上）

图像降噪算法——小波硬阈值滤波（上）

小波变换相对于傅里叶变换要更加抽象难以理解，其实到写这篇博客的时候我也没有完全理解小波变换，下面的基本介绍部分主要是根据《数字图像处理》和《A Tutorial of the Wavelet Transform》这两篇参考文献结合自己的理解过一遍推导过程，然后我基于OpenCV和FFWT库完成了一个简单的基于离散小波变换的图像降噪算法。

1. 多分辨率展开

在推导之前，首先需要引入一个思想，一个函数$f(x)$可以通过函数集合$\{{\phi }_k(x)\}$表示（展开），如下：$$f(x)=\sum _k{\alpha }_k{\phi }_k(x)$$如果基于函数集合$\{{\phi }_k(x)\}$展开方式唯一，则将${\phi }_k(x)$称为基函数，如果基函数满足：$$⟨{\phi }_j(x),{\phi }_k(x)⟩=\int {\phi }_j(x){\phi }_k(x{)}^{\ast }dx={\delta }_{jk}=\{\begin{array}{ll}0,& j\ne k\\ 1,& j=k\end{array}$$那么我们就可以通过积分来求解展开级数系数${\alpha }_k$：$$\begin{array}{rl}⟨f(x),{\phi }_k(x)⟩& =\int f(x){\phi }_k^{\ast }(x)dx\\ & =\int \left(\sum _{k^{\prime }}{\alpha }_{k^{\prime }}{\phi }_{k^{\prime }}(x)\right){\phi }_k^{\ast }(x)dx\\ & =\sum _{k^{\prime }}{\alpha }_{k^{\prime }}\left(\int {\phi }_{k^{\prime }}(x){\phi }_k^{\ast }(x)dx\right)\\ & =\sum _{k^{\prime }}{\alpha }_{k^{\prime }}{\delta }_{k^{\prime }k}\\ & ={\alpha }_k\end{array}$$基函数为${\phi }_k(x)=\exp (j2\pi kx/T)$的傅里叶级数展开就是上式的一个特例。

2. 尺度函数

尺度函数是定义为如下所示的一组函数的集合：$${\phi }_{j,k}(x)=2^{j/2}\phi \left(2^{j}x-k\right)$$其中，参数$j$决定了函数的宽度，参数$k$决定了函数的位置，这种操作可以理解为高中学的对函数的平移和缩放，以哈尔尺度函数为例：$$\phi (x)=\{\begin{array}{ll}1,& 0\le x<1\\ 0,& otherwise\end{array}$$那么$${\phi }_{0,0}(x)=\phi (x)=\{\begin{array}{ll}1,& 0\le x<1\\ 0,& otherwise\end{array}$$$${\phi }_{0,1}(x)=\phi (x-1)=\{\begin{array}{ll}1,& 1\le x<2\\ 0,& otherwise\end{array}$$$${\phi }_{1,0}(x)=\sqrt{2}\phi (2x)=\{\begin{array}{ll}\sqrt{2},& 0\le x<\frac{1}{2}\\ 0,& otherwise\end{array}$$$${\phi }_{1,1}(x)=\sqrt{2}\phi (2x-1)=\{\begin{array}{ll}\sqrt{2},& \frac{1}{2}\le x<1\\ 0,& otherwise\end{array}$$以此类推。

将缩放固定，平移变化（参数 $j$ 相同，参数 $k$ 不同）的一组函数构建为一个函数子集合$V_j$：
$$V_j=\overline{\mathrm{Span}}\left\{{\phi }_{j,k}(x)\right\}$$其中，$j$越大，缩放后的函数子集合中的函数越“窄”，则代表的细节越多。且“宽”函数子集合可以由“窄”函数子集合表示，即$V_j$可以由$V_{j+1}$表示，同样以哈尔尺度函数为例，我们可以发现：$${\phi }_{0,0}(x)=\frac{1}{\sqrt{2}}{\phi }_{1,0}(x)+\frac{1}{\sqrt{2}}{\phi }_{1,1}(x)$$对$V_0$和$V_1$两个函数子集合有：$${\phi }_{0,k}(x)=\frac{1}{\sqrt{2}}{\phi }_{1,2k}(x)+\frac{1}{\sqrt{2}}{\phi }_{1,2k+1}(x)$$这种关系可以用递推关系式表示为：$$\phi (x)=\sum _n{h}_{\phi }(n)\sqrt{2}\phi (2x-n)$$其中，$h_{\phi }(n)$成为尺度函数系数，同样是上面的哈尔尺度函数，我们已知$h_{\phi }(0)=h_{\phi }(1)=1/\sqrt{2}$，$V_0$和$V_1$两个函数子集合的关系就可以通过递推关系式直接获得：$$\phi (x)=\frac{1}{\sqrt{2}}[\sqrt{2}\phi (2x)]+\frac{1}{\sqrt{2}}[\sqrt{2}\phi (2x-1)]=\phi (2x)+\phi (2x-1)$$那么$h_{\phi }(n)$怎么求呢？对于不同的尺度函数是不同的，哈尔尺度函数的尺度函数系数就可以通过公式直接计算出来，即哈尔变换矩阵的计算公式，书上有且有一丢丢复杂，在此就不进行赘述。

3. 小波函数

小波函数是定义为如下所示的一组函数的集合：$${\psi }_{j,k}(x)=2\sqrt[j/2]{\psi \left(2^{j}x-k\right)}$$仿照上面尺度函数，我们同样定义一个函数子集合：$$W_j=\overline{\mathrm{Span}}\left\{{\psi }_{j,k}(x)\right\}$$小波函数子集合$W_j$和尺度函数子集合$V_j$之间的关系为（非常重要）是：$$V_{j+1}=V_j\oplus W_j$$其中，$\oplus$是并集符号，$V_{j+1}$和$V_j$的正交补集是$W_j$，且$V_j$中的所有函数$W_j$中的所有函数都正交，这种关系我们可以用这样一张图表示：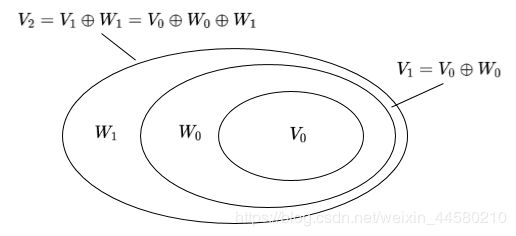
前面我们知道，即$V_j$可以由$V_{j+1}$表示，那么同样的道理，即$W_j$也可以由$V_{j+1}$表示，因此我们可以获得和尺度函数类似的递推关系式：$$\psi (x)=\sum _n{h}_{\psi }(n)\sqrt{2}\phi (2x-n)$$其中$h_{\psi }(n)$为小波函数系数，并且和尺度函数系数有如下关系：$$h_{\psi }(n)=(-1{)}^n{h}_{\phi }(1-n)$$还是以上面的哈尔尺度函数为例，我们来推导哈尔小波函数：
我们已知$h_{\phi }(0)=h_{\phi }(1)=1/\sqrt{2}$，那么根据上式有$$h_{\psi }(0)=(-1{)}^0{h}_{\phi }(1-0)=1/\sqrt{2}$$$$h_{\psi }(1)=(-1{)}^1{h}_{\phi }(1-1)=-1/\sqrt{2}$$因此我们有：$$\psi (x)=\phi (2x)-\phi (2x-1)$$我们带入$j=0$,$k=0$时的哈尔尺度函数：$${\phi }_{0,0}(x)=\phi (x)=\{\begin{array}{ll}1,& 0\le x<1\\ 0,& otherwise\end{array}$$这样我们就可以推导出$j=0$,$k=0$时的哈尔小波函数：$${\psi }_{0,0}(x)=\psi (x)=\{\begin{array}{ll}1,& 0⩽x<0.5\\ -1,& 0.5⩽x<1\\ 0,& otherwise\end{array}$$其他的小波函数可以按照同样的方式进行递推。

4. 小波级数展开

有了上面的铺垫，这里就可以给出小波级数展开的公式：$$f(x)=\sum _k{c}_{j_0}(k){\phi }_{j_0,k}(x)+\sum _{j=j_0}^{\infty }\sum _k{d}_j(k){\psi }_{j,k}(x)$$其中，${\phi }_{j_0,k}(x)$和${\psi }_{j,k}(x)$就是前面介绍的尺度函数和小波函数。$c_{j_0}(k)$和$d_j(k)$就是前面提到的尺度系数和小波系数（注意区分尺度函数系数和小波函数系数）。很幸运的是我们的尺度函数和小波函数满足1.1节中介绍的多分辨率展开条件，因此有：$$c_{j_0}(k)=⟨f(x),{\phi }_{j_0,k}(x)⟩=\int f(x){\phi }_{j_0,k}(x)\mathrm{d}x$$$$d_j(k)=⟨f(x),{\psi }_{j,k}(x)⟩=\int f(x){\psi }_{j,k}(x)\mathrm{d}x$$这里可能会有疑问，为什么小波函数的参数$j$是从$j_0$到$\infty$，而尺度函数的参数$j$仅仅为$j_0$？ 这个问题可以通过上面提到的小波函数子集合$W_j$和尺度函数子集合$V_j$之间的关系去理解，因为任何一个函数$f(x)$都最终可以由$V_0\oplus W_0\oplus W_1\oplus W_2\oplus \cdot \cdot \cdot$这样一个函数集合表示，尺度函数子集合$V_0$ 中的函数即${\phi }_{j0,k}(x)$，而$W_0$、$W_1\cdot \cdot \cdot$这样的小波函数子集合中的函数即${\psi }_{0,k}$、${\psi }_{1,k}\cdot \cdot \cdot$

这里紧接着上面的哈尔尺度函数和哈尔小波函数的例子进行小波级数展开，给定函数：$$y=\{\begin{array}{ll}{x}^2,& 0⩽x⩽1\\ 0,& otherwise\end{array}$$那么按照上面的公式有：$$c_0(0)={\int }_0^1{x}^2{\phi }_{0,0}(x)\mathrm{d}x={\int }_0^1{x}^2\mathrm{d}x={\frac{x^3}{3}|}_0^1=\frac{1}{3}$$$$d_0(0)={\int }_0^1{x}^2{\psi }_{0,0}(x)\mathrm{d}x={\int }_0^{05}{x}^2\mathrm{d}x-{\int }_{05}^1{x}^2\mathrm{d}x=-\frac{1}{4}$$$$d_1(0)={\int }_0^1{x}^2{\psi }_{1,0}(x)\mathrm{d}x={\int }_0^{0.25}{x}^2\sqrt{2}\mathrm{d}x-{\int }_{0.25}^{0.5}{x}^2\sqrt{2}\mathrm{d}x=-\frac{\sqrt{2}}{32}$$$$d_1(1)={\int }_0^1{x}^2{\psi }_{1,1}(x)\mathrm{d}x={\int }_{05}^{0.75}{x}^2\sqrt{2}\mathrm{d}x-{\int }_{0.75}^1{x}^2\sqrt{2}\mathrm{d}x=-\frac{3\sqrt{2}}{32}$$因此次函数的小波级数展开为：$$y=\underset{V_0}{\frac{1}{3}{\phi }_{0,0}(x)}+\underset{W_0}{[-\frac{1}{4}{\psi }_{0,0}(x)}+\underset{W_1}{\left[-\frac{\sqrt{2}}{32}{\psi }_{1,0}(x)-\frac{3\sqrt{2}}{32}{\psi }_{1,1}(x)\right]}+\cdots$$

5. 离散小波变换

离散小波变换就是用小波级数展开中小波系数和尺度系数在“小波域”中描述函数，相当于傅里叶变换后频域中的幅值和相角，因为是离散数据，所以需要通过加权求和的方式来代替积分，和如下图所示

其中$W_{\phi }\left(j_0,k\right)$就相当于$c_{j_0}(k)$，$W_{\psi }(j,k)$相当于$d_j(k)$，参考0小波级数展开，那么正向变换为：$$W_{\phi }\left(j_0,k\right)=\frac{1}{\sqrt{M}}\sum _{n}f(n){\phi }_{j_0,k}(n)$$$$W_{\psi }(j,k)=\frac{1}{\sqrt{M}}\sum _{n}f(n){\psi }_{j,k}(n),j⩾j_0$$而反向变换为：$$f(n)=\frac{1}{\sqrt{M}}\sum _k{W}_{\phi }\left(j_0,k\right){\phi }_{j_0,k}(n)+\frac{1}{\sqrt{M}}\sum _{j=j_0}^{\infty }\sum _k{W}_{\psi }(j,k){\psi }_{j,k}(n)$$其中${\phi }_{j0,k}(n)$和${\psi }_{j,k}(n)$是${\phi }_{j0,k}(x)$和${\psi }_{j,k}(x)$的采样形式，即$${\phi }_{j_0,k}(n)={\phi }_{j_0,k}\left(x_s+n\Delta x_s\right)$$$${\psi }_{j,k}(n)={\psi }_{j,k}\left(x_s+n\Delta x_s\right)$$$n=0,1,2,\cdots M-1$，$j=0,1,2,\cdots J-1$，其中$M$和$J$是有关系的，即$M=2^J$，我们可以这么说，变换是由$M$个系数组成的，最小尺度为$0$，最大尺度为$J-1$，起始位置$x_s$和位置间隔$\Delta x_s$是可以人为选择的，选择方法通常是使得采样点能够均匀分布到基函数的支撑区，具体怎么操作看下面的例子：

承接上面的例子，给定离散函数$f(0)=1,f(1)=4,f(2)=-3,f(3)=0$，我们以哈尔函数为基函数进行离散小波变换：
（1）首先由给定的采样值我们知道$M=4$，那么$J=2$，因此我们采用的哈尔尺度函数是${\phi }_{0,0}(x)$，采用的哈尔小波函数是${\psi }_{0,0}(x)$，${\psi }_{1,0}(x)$，${\psi }_{1,1}(x)$，前面已经推导过这些函数的表达式。
（2）接下来就是选择$x_s$和$\Delta x_s$了，哈尔函数的支撑区为$0$到$1$，因此我们就在区间$0$到$1$中选取四个采样点进行离散小波变换，例如令$x_s=0.2,\Delta x_s=0.2$，那么四个采样点为$x_0=0.2,x_1=0.4,x_2=0.6,x_3=0.8$，带入正向变换公式有：$$W_{\phi }(0,0)=\frac{1}{2}\sum _{n=0}^{3}f(n){\phi }_{0,0}(x_n)=\frac{1}{2}[1\cdot 1+4\cdot 1-3\cdot 1+0\cdot 1]=1$$$$W_{\psi }(0,0)==\frac{1}{2}\sum _{n=0}^{3}f(n){\psi }_{0,0}(x_n)=\frac{1}{2}[1\cdot 1+4\cdot 1-3\cdot (-1)+0\cdot (-1)]=4$$$$W_{\psi }(1,0)==\frac{1}{2}\sum _{n=0}^{3}f(n){\psi }_{1,0}(x_n)=\frac{1}{2}[1\cdot \sqrt{2}+4\cdot (-\sqrt{2})-3\cdot 0+0\cdot 0]=-1.5\sqrt{2}$$$$W_{\psi }(1,1)==\frac{1}{2}\sum _{n=0}^{3}f(n){\psi }_{1,1}(x_n)=\frac{1}{2}[1\cdot 0+4\cdot 0-3\cdot \sqrt{2}+0\cdot (-\sqrt{2})]=-1.5\sqrt{2}$$那么同样地，反向变换：$$f(0)=\frac{1}{2}\left[W_{\phi }(0,0){\phi }_{0,0}(x_0)+W_{\psi }(0,0){\psi }_{0,0}(x_0)+W_{\psi }(1,0){\psi }_{1,0}(x_0)+W_{\psi }(1,1){\psi }_{1,1}(x_0)\right]=\frac{1}{2}[1\cdot 1+4\cdot 1-1.5\sqrt{2}\cdot (\sqrt{2})-1.5\sqrt{2}\cdot 0]=1$$$f(1)$、$f(2)$、$f(3)$的反向变换操作以此类推。

6. 快速小波变换

以离散小波变换的正向变换为例，说白了我们就像想要获得的一些列小波系数$W_{\psi }(j,k)$和尺度系数$W_{\phi }\left(j_0,k\right)$，而我们在上面离散小波变换中的算法是将带变换的函数$f(n)$与尺度函数${\phi }_{j0,k}(n)$和小波函数${\psi }_{j,k}(n)$进行內积（加权求和）操作，这样计算量为$O\left(M^2\right)$,那么我们有什么办法可以更加快速地获得$W_{\psi }(j,k)$和$W_{\phi }\left(j_0,k\right)$吗？

答案就是快速小波变换，快速小波变换的基础如下：$$W_{\psi }(j,k)={h_{\psi }(-n)\star W_{\phi }(j+1,n)|}_{n=2k,k⩾0}$$$$W_{\phi }(j,k)={h_{\phi }(-n)\star W_{\phi }(j+1,n)|}_{n=2k,k⩾0}$$公式的推导过程可以参考《数字图像处理》，其中，$\star$是卷积符号，尺度函数系数$h_{\psi }(n)$和小波函数系数$h_{\phi }(n)$前文提到过可以直接通过公式计算，最高尺度系数$W_{\phi }(J,n)$我们假定为函数本身的采样值$f(n)$，那么我们就可以通过卷积以及下采样过程，一层一层地求解$W_{\psi }(j,k)$和$W_{\phi }(j,k)$，流程如下图所示：

这中间注意两点：
（1）已知$h_{\psi }(n)$和$h_{\phi }(n)$，那么与$h_{\psi }(-n)$和$h_{\phi }(-n)$卷积其实就是将已知的$h_{\psi }(n)$和$h_{\phi }(n)$翻转后再卷积；
（2）公式中 的$n=2k$指的是卷积操作是在$n=2k$是进行的，因此在卷积完成后还需要进行以2为基的下采样。
这样说可能还是比较抽象，举个例子就好了，还是离散小波变换中同样的例子：

给定离散函数$f(0)=1,f(1)=4,f(2)=-3,f(3)=0$以哈尔函数为基函数进行离散小波变换：

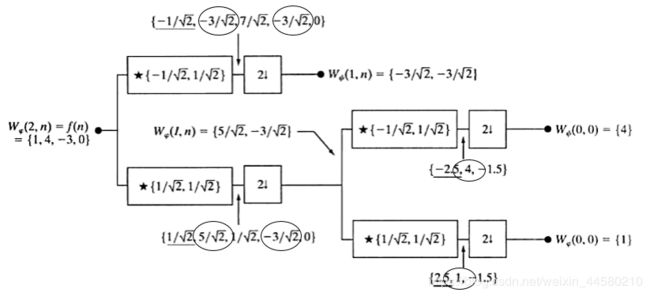
按照快速小波变换给出的算法我们可以画出上图所示的计算流程图，以$W_{\psi }(1,n)$的计算过程为例，首先进行卷积操作卷积操作，我们已知$h_{\phi }(0)=h_{\phi }(1)=1/\sqrt{2}，h_{\psi }(0)=1/\sqrt{2}，h_{\psi }(1)=-1/\sqrt{2}$，那么：$$h_{\psi }(-n)\star W_{\phi }(2,n)=h_{\psi }(-n)\star f(n)=\{-1/\sqrt{2},1/\sqrt{2}\}\star \{1,4,-3,0\}=\{-1/\sqrt{2},-3/\sqrt{2},7/\sqrt{2},-3/\sqrt{2},0\}$$这里解释下，因为$h_{\psi }(-n)$需要将$h_{\psi }(n)$翻转后当做卷积核，因此是$\{-1/\sqrt{2},1/\sqrt{2}\}$，卷积时需要将卷积核翻转后再逐位相乘，因此获得上面的结果。然后进行以2为基的下采样，就可以获得$W_{\psi }(1,n)=\{-3/\sqrt{2},-3/\sqrt{2}\}$，在图中下采样过程用椭圆进行了标注。

7. 图像小波变换

终于算是切入这篇博客的正题了，图像的小波变换中需要用到二维尺度函数和二维小波函数，它们其实就是通过一维尺度函数和一维小波函数乘积获得的，一共有一个二维尺度函数：$$\phi (x,y)=\phi (x)\phi (y)$$和三个二维小波函数：$$\begin{array}{rl}& {\psi }^H(x,y)=\psi (x)\phi (y)\\ & {\psi }^V(x,y)=\phi (x)\psi (y)\\ & {\psi }^D(x,y)=\psi (x)\psi (y)\end{array}$$其中${\psi }^H$是度量图像沿列方向的变化，${\psi }^V$是度量图像沿行方向的变化，${\psi }^D$是度量图像沿对角线方向的变化，这里首先给出二维尺度函数和二维小波函数公式：$${\phi }_{j,m,n}(x,y)=2^{j/2}\phi \left(2^{j}x-m,2^{j}y-n\right)$$$${\psi }_{j,m,n}^i(x,y)=2^{j/2}{\psi }^i\left(2^{j}x-m,2^{j}y-n\right),i=\{H,V,D\}$$那么$M\times N$图像的小波变换的正向变换为：$$W_{\phi }\left(j_0,m,n\right)=\frac{1}{\sqrt{MN}}\sum _{x=0}^{M-1}\sum _{y=0}^{N-1}f(x,y){\phi }_{j_0,m,n}(x,y)$$$$W_{\psi }^i(j,m,n)=\frac{1}{\sqrt{MN}}\sum _{x=0}^{M-1}\sum _{y=0}^{N-1}f(x,y){\psi }_{j,m,n}^i(x,y),i=\{H,V,D\}$$反向变换为$$\begin{array}{rl}f(x,y)=& \frac{1}{\sqrt{MN}}\sum _m\sum _n{W}_{\phi }\left(j_0,m,n\right){\phi }_{j_0,m,n}(x,y)+\\ & \frac{1}{\sqrt{MN}}\sum _{i=H,V}\sum _{j=j_0}^{\infty }\sum _m\sum _n{W}_{\psi }^i(j,m,n){\psi }_{j,m,n}^i(x,y)\end{array}$$这几个求和符号一叠加就知道二维离散小波变换计算量肯定不小，因此在实际操作中采用的更多是二维快速小波变换，其原理和上面介绍的一维快速小波变换一致，先卷积，然后下采样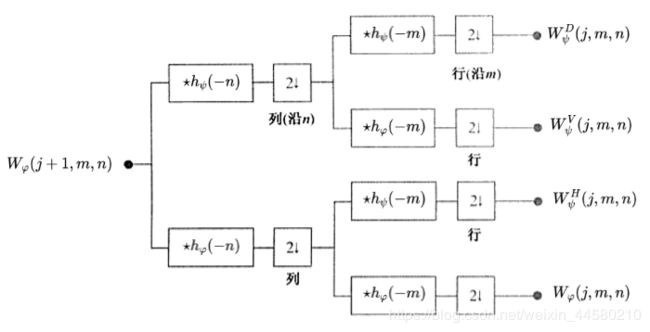：这里需要注意的是：
（1）卷积是先按列进行，然后再按行进行
（2）因为是以2为基的下采样，因此会导致经过小波变换后的图像分辨率以2为因子下降，因此小波变换后输出的图像如下所示：
原始图像：

$J=1$时的小波变换：

$J=2$时的小波变换：

$J=3$时的小波变换：

这篇博客主要按照《数字图像处理》一书中的思路循序渐进地推导了小波离散变换以及将其应用到图像上，如果想知道如何利用OpenCV和FFWT库实现上面的图像小波变换，以及如果利用小波变换对图像进行降噪，请参考：

图像降噪算法——离散小波变换（下）

那么这个篇博客就先到此为止，欢迎交流～