0x6A.图论 - 网络流初步

声明：
本系列博客是《算法竞赛进阶指南》+《算法竞赛入门经典》+《挑战程序设计竞赛》的学习笔记，主要是因为我三本都买了 按照《算法竞赛进阶指南》的目录顺序学习，包含书中的少部分重要知识点、例题解题报告及我个人的学习心得和对该算法的补充拓展，仅用于学习交流和复习，无任何商业用途。博客中部分内容来源于书本和网络（我尽量减少书中引用），由我个人整理总结（习题和代码可全都是我自己敲哒）部分内容由我个人编写而成，如果想要有更好的学习体验或者希望学习到更全面的知识，请于京东搜索购买正版图书：《算法竞赛进阶指南》——作者李煜东，强烈安利，好书不火系列，谢谢配合。

---

下方链接为学习笔记目录链接（中转站）

学习笔记目录链接

---

ACM-ICPC在线模板

---

真的只是网络流初步。

一、网络流基本概念

网络流:所有弧上流量的集合$f=f(u,v)$,称为该容量网络的一个网络流.

定义：带权的有向图$G=(V,E)$，满足以下条件，则称为网络流图($flownetwork$)：

• 仅有一个入度为0的顶点s，称s为源点
• 仅有一个出度为0的顶点t，称t为汇点
• 每条边的权值都为非负数，称为该边的容量，记作$c(i,j)$。特别地，如果$(x,y)\notin E$，则$C(x,y)=0$。

弧的流量:通过容量网络G中每条弧< u,v>,上的实际流量(简称流量),记为$f(u,v)$，$c(x,y)-f(x,y)$称作边的剩余容量。

性质
对于任意一个时刻，设f(u,v)实际流量，则整个图G的流网络满足3个性质：

• 容量限制：对任意$u,v\in V，f(u,v)\le c(u,v)$。
• 反对称性：对任意$u,v\in V，f(u,v)=-f(v,u)$。从u到v的流量一定是从v到u的流量的相反值。
• 流守恒性：对任意u，若u不为S或T，一定有${\sum }_{(u,x)\in E}f(u,x)={\sum }_{(x,v)\in E}f(x,v)$。流入u的流量和u点流出的流量相等，u点本身不会”制造”和”消耗”流量。

可行流 :在容量网络G中满足以下条件的网络流f,称为可行流.

• 弧流量限制条件: $0<=f(u,v)<=c(u,v)$;

• 平衡条件:即流入一个点的流量要等于流出这个点的流量,(源点和汇点除外).

零流 :若网络流上每条弧上的流量都为0,则该网络流称为零流.

伪流:如果一个网络流只满足弧流量限制条件,不满足平衡条件,则这种网络流为伪流,或称为容量可行流.(在预流推进优化算法中使用)

二、最大流

对于网络流图G，流量最大的可行流f，称为最大流,此时的流量被称作最大流量。

最大流算法可以解决很多实际的问题，比如二分图的最大匹配数就等于网络的最大流量。因此我们可以使用dinic算法或者EK算法优化匈牙利算法。求出最大流以后，所有有"流"经过的点、边就是匹配点、匹配边。

下面是所有最大流算法的精华部分：引入反向边
为什么要有反向边呢？

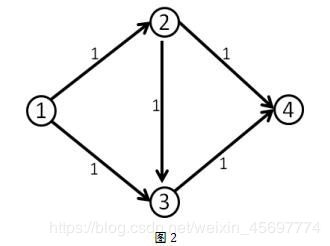
我们第一次找到了1-2-3-4这条增广路，这条路上的delta值显然是1。于是我们修改后得到了下面这个流。（图中的数字是容量）

这时候(1,2)和(3,4)边上的流量都等于容量了，我们再也找不到其他的增广路了，当前的流量是1。

但这个答案明显不是最大流，因为我们可以同时走1-2-4和1-3-4，这样可以得到流量为2的流。

那么我们刚刚的算法问题在哪里呢？问题就在于我们没有给程序一个”后悔”的机会，应该有一个不走(2-3-4)而改走(2-4)的机制。那么如何解决这个问题呢？回溯搜索吗？那么我们的效率就上升到指数级了。

而这个算法神奇的利用了一个叫做反向边的概念来解决这个问题。即每条边(I,j)都有一条反向边(j,i)，反向边也同样有它的容量。

我们直接来看它是如何解决的：

在第一次找到增广路之后，在把路上每一段的容量减少delta的同时，也把每一段上的反方向的容量增加delta。即在Dec(c[x,y],delta)的同时，inc(c[y,x],delta)

我们来看刚才的例子，在找到1-2-3-4这条增广路之后，把容量修改成如下

这时再找增广路的时候，就会找到1-3-2-4这条可增广量，即delta值为1的可增广路。将这条路增广之后，得到了最大流2。

那么，这么做为什么会是对的呢？我来通俗的解释一下吧。

事实上，当我们第二次的增广路走3-2这条反向边的时候，就相当于把2-3这条正向边已经是用了的流量给”退”了回去，不走2-3这条路，而改走从2点出发的其他的路也就是2-4。（有人问如果这里没有2-4怎么办，这时假如没有2-4这条路的话，最终这条增广路也不会存在，因为他根本不能走到汇点）同时本来在3-4上的流量由1-3-4这条路来”接管”。而最终2-3这条路正向流量1，反向流量1，等于没有流量。

这就是这个算法的精华部分，利用反向边，使程序有了一个后悔和改正的机会

1）$Edmonds-Karp$算法

若一条从源点到汇点的路径上各条边的剩余容量都大于0，则称这条路径为一条增广路。

Edmonds-Karp增广路的策略就是不断用bfs寻找增广路，直至网络中不在存在增广路为止。

在每次寻找增广路的过程中，EK算法只考虑图中所有$f(x,y)<c(x,y)$即剩余容量大于0的边。这样用bfs寻找增广路，并计算路径上各边剩余容量的最小值minf，最后网络的流量就可以增加minf。（想象成水管，最后只能流出所有管道里口径最小的流量。）

但是当一条边的流量$f(x,y)>0$时，根据斜对称性质，它的反向边流量$f(x,y)<0$，则必有$f(x,y)<c(x,y)$，因此我们还需要考虑每条边的反向边。

因此我们利用成对变换技巧，每条边只记录剩余流量$c-f$即可，当一条边$(x,y)$流过大小为e的流时，令$(x,y)$的剩余流量减少e，$(y,x)$的剩余流量增加$e$ (想一想，为什么)

$Edmonds-Karp$的时间复杂度为$O(n{m}^2)$，但是在实际运用时效率往往很高，一般能处理$10^3$~ $10^4$规模的网络。

luogu P2740草地排水 Edmonds-Karp增广路，最大流模板

题目链接：草地排水

根据上述EK算法思路实现的AC模板代码：

#include
#include
#include
#include
#include
#include
#include
#include
#define ls (p<<1)
#define rs (p<<1|1)
#define over(i,s,t) for(register int i = s;i <= t;++i)
#define lver(i,t,s) for(register int i = t;i >= s;--i)
//#define int __int128
#define lowbit(p) p&(-p)
using namespace std;

typedef long long ll;
typedef pair<int,int> PII;
const int INF = 0x3f3f3f3f;
const int N = 2e3+7;
const int M = 5e3+7;

int head[N],nex[M],ver[M],tot = 1,edge[M];
int vis[N],incf[N],pre[N];
int n,m,s,t,maxflow;

void add(int x,int y,int z){//建正边和反边
    ver[++tot] = y;edge[tot] = z;nex[tot] = head[x];head[x] = tot;
    ver[++tot] = x;edge[tot] = 0;nex[tot] = head[y];head[y] = tot;
}

bool bfs(){//bfs找增广路
    memset(vis,0,sizeof vis);
    queue<int>q;
    q.push(s);
    vis[s] = 1;
    incf[s] = INF;//增广路上各边的最小剩余容量
    while(q.size()){
        int x = q.front();
        q.pop();
        for(int i = head[x];i;i = nex[i]){
            if(edge[i]){//只有剩余容量>0才往下走
                int y = ver[i];
                if(vis[y])continue;
                incf[y] = min(incf[x],edge[i]);
                pre[y] = i;//存前驱，用于找到最长路的实际方案
                q.push(y);vis[y] = 1;
                if(y == t)return 1;
            }
        }
    }
    return 0;
}

void update(){//更新增广路及其反向边的剩余容量
    int x = t;
    while(x != s){
        int i = pre[x];
        edge[i] -= incf[t];
        edge[i ^ 1] += incf[t];
        x = ver[i ^ 1];//成对变换
    }
    maxflow += incf[t];
}

int main(){
    while(cin>>m>>n){
        memset(head,0,sizeof head);
        s = 1,t = n;tot = 1;maxflow = 0;
        over(i,1,m){
            int x,y,z;
            scanf("%d%d%d",&x,&y,&z);
            add(x,y,z);
        }
        while(bfs())
            update();
        printf("%d\n",maxflow);
    }
    return 0;
}

2）$Dinic$算法

Dinic算法是网络流最大流的优化算法之一，每一步对原图进行分层，然后用DFS求增广路。时间复杂度是O(n^2*m)，Dinic算法最多被分为n个阶段，每个阶段包括建层次网络和寻找增广路两部分。
Dinic算法的思想是分阶段地在层次网络中增广。它与最短增广路算法不同之处是：最短增广路每个阶段执行完一次BFS增广后，要重新启动BFS从源点Vs开始寻找另一条增广路;而在Dinic算法中，只需一次DFS过程就可以实现多次增广。

层次图：

层次图，就是把原图中的点按照点到源的距离分“层”，只保留不同层之间的边的图。

算法流程：

1、根据残量网络计算层次图。
2、在层次图中使用DFS进行增广直到不存在增广路。
3、重复以上步骤直到无法增广。

实现

首先对每条弧存一条反向弧，初始流量为0，当正向弧剩余流量减少时，反向弧剩余流量随之增加，这样就为每条弧提供了一个反悔的机会，可以让一个流沿反向弧退回而去寻找更优的路线。对于一个网络流图，用bfs将图分层，只保留每个点到下一个层次的弧，目的是减少寻找增广路的代价。对于每一次可行的增广操作，用dfs的方法寻找一条由源点到汇点的路径并获得这条路径的流量c。根据这条路径修改整个图,将所经之处正向边流量减少c，反向边流量增加c。如此反复直到bfs找不到可行的增广路线。

当前弧优化：

对于一个节点x，当它在dfs中走到了第i条弧时，前i-1条弧到汇点的流一定已经被流满而没有可行的路线了。那么当下一次再访问x节点的时候，前i-1条弧就可以被删掉而没有任何意义了。所以我们可以在每次枚举节点x所连的弧时，改变枚举的起点，这样就可以删除起点以前的所有弧以达到优化的效果。

本题增强了数据，时间更是卡到了500ms，以前的好多题解都过不去了。
有一个问题是我使用弧优化最后两个点跑了750ms T 了，但是我把弧优化去掉了以后只跑了60ms，成功AC，真是很玄学。

我知道哪里的问题了，蓝书《算法竞赛进阶指南》上的弧优化好像有点问题，now[x] = i好像应该放到for循环里面，我参照的洛谷日报上的写法，跑了最后一个点只13ms。蓝书的写法可能会让第i条边还有剩余容量时直接被跳过，所以要写到里面。（评论区的大佬说的）

#include
#include
#include
#include
#include
#include
//#define ls (p<<1)
//#define rs (p<<1|1)
#define over(i,s,t) for(register int i = s;i <= t;++i)
#define lver(i,t,s) for(register int i = t;i >= s;--i)
//#define int __int128
//#define lowbit(p) p&(-p)
using namespace std;

typedef long long ll;
typedef pair<int,int> PII;
const ll INF = 1e18;
const int N = 5e2+7;
const int M = 2e5+7;

int head[N],nex[M],ver[M],tot = 1;
ll edge[M];
int n,m,s,t;
ll maxflow;
ll deep[N];//层级数，其实应该是level
int now[M];//当前弧优化
queue<int>q;

inline void read(int &x){
    int f=0;x=0;char c=getchar();
    while(c<'0'||c>'9')f|=c=='-',c=getchar();
    while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
    x=f?-x:x;
}

inline void add(int x,int y,int z){//建正边和反向边
    ver[++tot] = y;edge[tot] = z;nex[tot] = head[x];head[x] = tot;
    ver[++tot] = x;edge[tot] = 0;nex[tot] = head[y];head[y] = tot;
}

inline bool bfs(){//在残量网络中构造分层图
    over(i,1,n)deep[i] = INF;
    while(!q.empty())q.pop();
    q.push(s);deep[s] = 0;now[s] = head[s];//一些初始化
    while(!q.empty()){
        int x = q.front();q.pop();
        for(int i = head[x];i;i = nex[i]){
            int y = ver[i];
            if(edge[i] > 0 && deep[y] == INF){//没走过且剩余容量大于0
                q.push(y);
                now[y] = head[y];//先初始化，暂时都一样
                deep[y] = deep[x] + 1;
                if(y == t)return 1;//找到了
            }
        }
    }
    return 0;
}

//flow是整条增广路对最大流的贡献，rest是当前最小剩余容量，用rest去更新flow
ll dfs(int x,ll flow){//在当前分层图上增广
    if(x == t)return flow;
    ll ans = 0,k,i;
    for(i = now[x];i && flow;i = nex[i]){
        now[x] = i;//当前弧优化（避免重复遍历从x出发的不可拓展的边）
        int y = ver[i];
        if(edge[i] > 0 && (deep[y] == deep[x] + 1)){//必须是下一层并且剩余容量大于0
            k = dfs(y,min(flow,edge[i]));//取最小
            if(!k)deep[y] = INF;//剪枝，去掉增广完毕的点
            edge[i] -= k;//回溯时更新
            edge[i ^ 1] += k;//成对变换
            ans += k;
            flow -= k;
        }
        //if(!flow)return rest;
    }

    return ans;
}

void dinic(){
    while(bfs())
        maxflow += dfs(s,INF);
}

int main()
{
    read(n);read(m);read(s);read(t);
    tot = 1;//成对变换
    over(i,1,m){
        int x,y,z;
        read(x);read(y);read(z);
        add(x,y,z);
    }
    dinic();
    printf("%lld\n",maxflow);
    return 0;
}

三、最小割

UVA1660 电视网络 Cable TV Network（网络流，最小割）

题目链接

题意翻译
电视电缆网络的继电器之间的连接是双向的。如果任意两个继电器之间都连通，那么这个网络就是连通的，否则不连通。特别地，一个空网络或只有一个继电器的网络是连通的。
定义一个有n个继电器的网络的安全指数f为
如果不管移除几个继电器，网络都连通，f=n
使网络不连通至少要移除的继电器数
给出t(t≤20)个网络，求每个网络的安全指数(每个网络的继电器数≤50)。

枚举两个不直接连通的点 S 和 T ，求在剩余的 n−2 个节点中最少去掉多少个可以使 S 和 T 不连通，在每次枚举的结构中取 min 就是本题的答案。

运用点边转化技巧

把原来无向图中的每个点 x ，拆成入点 x 和出点 x′。在无向图中删去一个点⇔在网络中断开 (x,x′) 。对 $\forall x\ne S,x\ne T$
连有向边 (x,x′)，容量为 1 。对原无向图的每条边 (x,y) ，连有向边 (x’,y),(y’,x)，容量为 $+\infty$（防止割断）。

因为原来要删点，那么与这个点相连的若干条边都要切掉比较麻烦，那么直接将点 $x$ 转换为入点 $x$ 和出点 $x^{\prime }$ 并将他们连起来，这样在想要删掉x这个点的时候只需要将边$x->x^{\prime }$这一条边删掉即可。
最小割中设置容量为 $+\infty$ 的边具有“防止割断”的含义。

其他所有的相连的边都置为INF，标记不可割断，拆的是单个点自己和自己的入点和出点的边。

#include
#include
#include
#include
#include
#include
using namespace std;

typedef long long ll;
typedef pair<int,int> PII;
const int INF = 0x3f3f3f3f;
const int N = 100;
const int M = 5e4+7;

int s1,t1,n,m;
int head[N<<1],ver[M],nex[M],edge[M],tot;
int a[N * N],b[N * N],deep[N<<1];


inline void add(int x,int y,int z){//正边反边
    ver[++tot] = y;edge[tot] = z;
    nex[tot] = head[x];head[x] = tot;
    ver[++tot] = x;edge[tot] = 0;
    nex[tot] = head[y];head[y] = tot;
}

inline bool bfs(){
    memset(deep,0,sizeof deep);
    queue<int>q;
    q.push(s1);
    deep[s1] = 1;//分层
    while(q.size()){
        int x = q.front();
        q.pop();
        for(int i = head[x];i;i = nex[i]){
            int y = ver[i],z = edge[i];//剩余容量>0才属于残量网络
            if(z > 0 && !deep[y]){//不只是更新deep数组，是在残量网络上更新deep数组
                q.push(y);
                deep[y] = deep[x] + 1;
                if(y == t1)return true;
            }
        }
    }
    return false;
}

inline int dinic(int x,int flow){
    if(x == t1)return flow;
    int res = flow;
    for(int i = head[x];i && res;i = nex[i]){
        int y = ver[i],z = edge[i];
        if(z > 0 && (deep[y] == deep[x] + 1)){
            int k = dinic(y,min(res,z));
            if(!k)deep[y] = 0;
            edge[i] -= k;
            edge[i ^ 1] += k;
            res -= k;
        }
    }
    return flow - res;
}

int main(){
    while(cin>>n>>m){
        for(int i = 0;i < m;++i){
            char str[20];
            scanf("%s",str);
            a[i] = b[i] = 0;
            int j;
            for(j = 1;str[j] != ',';j++)
                a[i] = a[i] * 10 + (str[j] - '0');
            for(j++;str[j] != ')';j++)
                b[i] = b[i] * 10 + (str[j] - '0');
        }
        int ans = INF;
        for (s1 = 0; s1 < n; s1++)
		for (t1 = 0; t1 < n; t1++)
        if(s1 != t1){
            memset(head,0,sizeof head);
            tot = 1;
            int maxflow = 0;
            for(int i = 0;i < n;++i){
                if(i == s1 || i == t1)//i是入点,i+n是出点
                     add(i,i + n,INF);//防止被割断
                else add(i,i + n,1);
            }
            for(int i = 0;i < m;++i){
                add(a[i] + n,b[i],INF);//不能割
                add(b[i] + n,a[i],INF);
            }
            while(bfs()){
                int num;
                while((num = dinic(s1,INF)))
                    maxflow += num;
            }
            ans = min(ans,maxflow);
        }
        if(n <= 1 || ans == INF)ans = n;
        cout<<ans<<endl;
    }
    return 0;
}

四、费用流

luogu P2045 方格取数加强版（k取方格数）(最大费用最大流)

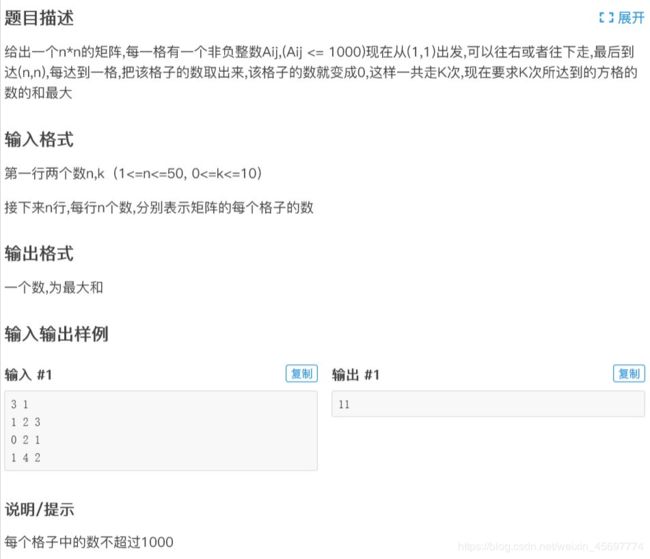
点边转化：把每个格子 (i,j) 拆成一个入点一个出点。
详解链接：【图论技巧】点边转化（拆点和拆边）
从每个入点向对应的出点连两条有向边：一条容量为 1 ，费用为格子 (i,j) 中的数；
另一条容量为 k−1 ，费用为 0 。

从 (i,j) 的出点到 (i,j+1) 和 (i+1,j) 的入点连有向边，容量为 k ，费用为 0 。
以 (1,1) 的入点为源点， (n,n) 的出点为汇点，求最大费用最大流。

#include
#include
#include
#include
#include
#include
//#define ls (p<<1)
//#define rs (p<<1|1)
#define over(i,s,t) for(register int i = s;i <= t;++i)
#define lver(i,t,s) for(register int i = t;i >= s;--i)
//#define int __int128
//#define lowbit(p) p&(-p)
using namespace std;

typedef long long ll;
typedef pair<int,int> PII;
const ll INF = 1e18;
const int N = 5e3+7;
const int M = 5e5+7;
int maxflow,s,t,k;
int n,m,ans,e;
int head[N],ver[M],nex[M],edge[M],cost[M],tot;
bool vis[N];
int dis[N],incf[N],pre[N];

void add(int x,int y,int z,int c){//正边反边
    ver[++tot] = y;edge[tot] = z;cost[tot] = c;
    nex[tot] = head[x];head[x] = tot;
    ver[++tot] = x;edge[tot] = 0;cost[tot] = -c;
    nex[tot] = head[y];head[y] = tot;
}

int num(int i,int j,int k){
    return (i - 1) * n + j + k * n * n;
}

bool spfa(){//spfa求最长路
    queue<int>q;
    memset(vis,0,sizeof vis);
    memset(dis,0xcf,sizeof dis);//-INF
    q.push(s);
    dis[s] = 0;vis[s] = 1;
    incf[s] = 1<<30;//增广路各边的最小剩余容量
    while(q.size()){
        int x = q.front();q.pop();
        vis[x] = 0;//spfa的操作
        for(int i = head[x];i;i = nex[i]){
            if(edge[i]){//剩余容量要>0,才在残余网络中
                int y = ver[i];
                if(dis[y] < dis[x] + cost[i]){
                    dis[y] = dis[x] + cost[i];
                    incf[y] = min(incf[x],edge[i]);//最小剩余容量
                    pre[y] = i;//记录前驱（前向星编号），方便找到最长路的实际方案
                    if(!vis[y])
                        vis[y] = 1,q.push(y);
                }
            }
        }
    }
    if(dis[t] == 0xcfcfcfcf)
        return false;//汇点不可达，已求出最大流
    return true;
}

//EK的老操作了,更新最长增广路及其反向边的剩余容量
void update(){
    int x = t;
    while(x != s){
        int i = pre[x];
        edge[i] -= incf[t];
        edge[i ^ 1] += incf[t];//成对变换,反边加
        x = ver[i ^ 1];//反边回去的地方就是上一个结点
    }
    maxflow += incf[t];//顺便求最大流
    ans += dis[t] * incf[t];//题目要求
}

void EK(){
    while(spfa())//疯狂找增广路
        update();
}

int main(){
    cin>>n>>k;
    s = 1;t = 2 * n * n;
    tot = 1;
    over(i,1,n)
    over(j,1,n){
        int c;
        scanf("%d",&c);
        add(num(i,j,0),num(i,j,1),1,c);//自己（入点0）与自己（出点1）
        add(num(i,j,0),num(i,j,1),k-1,0);//两条边（取k次嘛，第一次有值，以后就没值了，用作下次选取）
        if(i < n)add(num(i,j,1),num(i+1,j,0),k,0);//自己（出点1）与下一行（入点0）或者下一列（入点0）
        if(j < n)add(num(i,j,1),num(i,j+1,0),k,0);
    }
    EK();
    printf("%d\n",ans);
    return 0;
}