遗传算法解决TSP问题二(python实现)
上次尝试用简单的交叉变异方式编写了遗传算法,这次将使用启发式的交叉变异方式:
启发式交叉由Grefenstette, Gopal, Rosrnaita和Gucht首先提出。启发式交叉步骤(最近邻点法)为:
步骤1:从一对双亲中随机地选取一个城市作为开始城市;
步骤2:由当前城市出发,选择一条不构成循环的最短边(由双亲表达的)。若两条边都构成循环,则随机选取一个能使巡回继续的城市;
步骤3:如巡回完成,停机;否则转第2步。
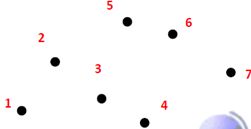
例如,对于如上的地图,随机选取城市3作为开始的城市,得到的子代为:

启发式变异由Cheng和Gen提出。采用邻域技术,以获得后代的改进。启发式变异过程如下:
步骤1:随机地选出λ个基因;
步骤2:按所有选出基因的可能的换位产生邻域;
步骤3:评估所有邻域点,选出最好的作为变异产生的后代。
示例:

下面给出启发式交叉变异方式解决TSP问题的完整代码:
import numpy as np
import random as rd
import matplotlib.pyplot as plt
"""计算染色体对应的路线总长"""
def countlen(chromo, distance, cityNum):
lenth = 0
for iii in range(cityNum - 1):
lenth += distance[chromo[iii]][chromo[iii + 1]]
lenth += distance[chromo[cityNum - 1]][chromo[0]] # 加上返回起点的距离
return lenth
"""生成初始种群"""
def crepopula(cityNum, M):
popula = [] # 种群
for ii in range(M):
chromo = np.random.permutation(cityNum).tolist() # 染色体
popula.append(chromo)
return popula
"""计算种群中每个个体的累积概率"""
def countprobabily(popula,distance,cityNum):
evall = []
for chromo in popula:
eval = max(30000 - countlen(chromo, distance,cityNum),0) # 适应值函数
evall.append(eval)
seval = sum(evall)
probabil = evall/seval #单个概率
probabily = probabil.copy()
for i in range(1,len(popula)):
probabily[i]=probabily[i]+probabily[i-1] #累积概率
return probabily
"""轮盘赌挑选子代个体"""
def lpd(popula,probabily,M):
newpopula=[]
for i in range(M):
proba = rd.random()
for ii in range(len(probabily)):
if probabily[ii] >= proba:
selechromo = popula[ii]
break
newpopula.append(selechromo)
return newpopula
"""启发式交叉:最近邻点法"""
def crossover_nn(father1, father2,cityNum,distance):
father_1 = father1.copy()
father_2 = father2.copy()
city0 = rd.randint(0, cityNum-1) #随机选择一个城市作为起始点
son = [city0]
while len(son) < len(father1):
ord1 = father_1.index(city0)
ord2 = father_2.index(city0)
if ord1 == len(father_1)-1 :
ord1 = -1
if ord2 == len(father_1)-1 :
ord2 = -1
city1 = father_1[ord1 + 1]
city2 = father_2[ord2 + 1]
father_1.remove(city0)
father_2.remove(city0)
if distance[city0][city1] <= distance[city0][city2]:
son.append(city1)
city0 = city1
else:
son.append(city2)
city0 = city2
return son
"""启发式变异"""
import itertools
def variat2(father,cityNum,distance):
or1 = rd.randint(0, cityNum - 1) #随机生成5个位置
or2 = rd.randint(0, cityNum - 1)
or3 = rd.randint(0, cityNum - 1)
or4 = rd.randint(0, cityNum - 1)
or5 = rd.randint(0, cityNum - 1)
nosame = list(set([or1, or2, or3, or4, or5]))
ords = list(itertools.permutations(nosame, len(nosame)))
sons = [] #将所有子代表示出来
sonn = father.copy()
for ord in ords:
for ii in range(len(nosame)):
sonn[nosame[ii]] = father[ord[ii]]
sons.append(sonn)
son_leng = [] #计算所有子代的距离
for sonn in sons:
leng = countlen(sonn, distance, cityNum)
son_leng.append(leng)
n = son_leng.index(min(son_leng)) #挑选最小距离
return sons[n]
def main():
M = 10 # 种群规模
cityNum = 52 # 城市数量,染色体长度
"""52个城市坐标位置"""
cities = [[565, 575],[25, 185],[345, 750],[945, 685],[845, 655],[880, 660],[25, 230],[525, 1000],[580, 1175],
[650, 1130],[1605, 620],[1220, 580],[1465, 200],[1530, 5],[845, 680],[725, 370],[145, 665],[415, 635],
[510, 875],[560, 365],[300, 465],[520, 585],[480, 415],[835, 625],[975, 580],[1215, 245],[1320, 315],
[1250, 400],[660, 180],[410, 250],[420, 555],[575, 665],[1150, 1160],[700, 580],[685, 595],[685, 610],
[770, 610],[795, 645],[720, 635],[760, 650],[475, 960],[95, 260],[875, 920],[700, 500],[555, 815],
[830, 485],[1170, 65],[830, 610],[605, 625],[595, 360],[1340, 725],[1740, 245]]
"""生成距离矩阵"""
distance = np.zeros([cityNum,cityNum])
for i in range(cityNum):
for j in range(cityNum):
distance[i][j] = pow((pow(cities[i][0]-cities[j][0],2)+pow(cities[i][1]-cities[j][1],2)),0.5)
"""初始化种群"""
popula = crepopula(cityNum, M)
for n in range(600): # 循环次数
"""种群进化"""
pc = 0.8 # 交叉率
pv = 0.25 # 变异率
son = []
##交叉
crossgroup = []
for i in range(M):
cpb = rd.random()
if cpb < pc: # 小于交叉率的进行交叉
crossgroup.append(popula[i])
if len(crossgroup) % 2 == 1: # 如果奇数个
del crossgroup[-1]
if crossgroup != []: # 启发式交叉
for ii in range(0, len(crossgroup), 2):
sonc = crossover_nn(crossgroup[ii], crossgroup[ii + 1], cityNum, distance)
son.append(sonc)
##变异
variatgroup = []
for j in range(M):
vpb = rd.random()
if vpb < pv: # 小于变异率的进行变异
variatgroup.append(popula[j])
if variatgroup != []:
for vag in variatgroup:
sonv = variat2(vag, cityNum, distance) #启发式变异
son.append(sonv)
"""计算每个染色体的累积概率"""
populapuls = popula + son
probabily = countprobabily(populapuls, distance, cityNum)
"""轮盘赌选择新种群"""
popula = lpd(populapuls, probabily, M)
"""挑选最好的染色体"""
opt_chr = popula[0]
opt_len = countlen(popula[0], distance, cityNum)
for chr in popula:
chrlen = countlen(chr, distance, cityNum)
if chrlen < opt_len:
opt_chr = chr
opt_len = chrlen
print("最优路径: " + str(opt_chr))
print("最优值:" + str(opt_len))
"""绘制地图"""
for cor in range(len(opt_chr)-1) :
x = [cities[opt_chr[cor]][0],cities[opt_chr[cor+1]][0]]
y = [cities[opt_chr[cor]][1],cities[opt_chr[cor+1]][1]]
plt.plot(x,y,"b-")
plt.show()
if __name__ =="__main__":
main()
输出结果:(已知最优解:7542)
此程序的最优总距离:10802.005083049522

由此,可见启发式算法收敛性能有所提高,并且能够跳出局部最优解,更好地找到全局最优解。收敛速度和收敛精度有了大大的提高。所以启发式遗传算法优于不加启发式的遗传算法。
备注:通过增大种群规模(程序中的M),可以使运算结果更接近已知最优解。