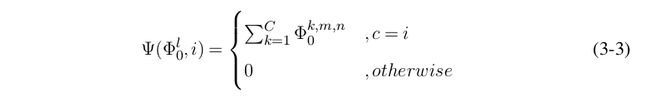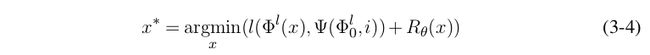小锐驿站

神经网络压缩 (总结6)

神经网络压缩

1.1神经网络压缩的必要性与可能性

深度学习的实际应用往往受限于其存储和运算规模。例如,VGG-16网络含有约1.4亿浮点数参数,假设每个参数存储为32位浮点数格式,则整个网络需要占用超过500兆存储空间。在运算时,单张测试图片共需要大约3.13 × 10 8 次浮点数运算。这样的计算量在目前只能通过高性能并行设备进行,且仍不具备很好的实时性。高性能并行计算设备具有体积大、能耗大、价格高的特点,在许多场合都不能使用。因此,如何在资源受限场合,如手机、平板电脑、各种嵌入式和便携式设备上运行神经网络,是深度学习走向日常生活的关键一步。

神经网络的压缩不但具有必要性，也具有可能性。首先，尽管神经网络通常是深度越深，效果越好，但针对具体的应用场景和需求，适当深度和参数数目的网络即能够满足。盲目加深网络复杂度所带来的微弱性能提升在许多应用场合意义并不大。其次，神经网络常常存在过参数化的问题，网络神经元的功能具有较大的重复性，即使在网络性能敏感的场景，大部分网络也可以被“安全地”压缩而不影响其性能。

神经网络压缩的方法

2.1 基于张量分解的网络压缩

张量是向量和矩阵的自然推广，向量可称为一阶张量，矩阵可称为二阶张量，将矩阵堆叠形成“立方体”，这种数据结构则称为三阶张量。一张灰度图像在计算机中由矩阵表示，是二阶张量。一张RGB三通道的彩色图像在计算机中则保存为三阶张量。当然，三阶张量也可以堆叠形成更高阶的张量。张量分解是张量分析中的重要组成部分，其基本原理是利用张量数据中的结构信息，将张量分解为形式更简单、存储规模更小的若干张量的组合。典型的张量分解方法有CP分解，Tucker分解等。
在神经网络中，参数通常以“张量”的形式集中保存。对全连接层而言，全连接通过权重矩阵将输入向量变换到输出向量，其参数为二阶张量。对卷积层而言，设输入数据为具有?通道的三阶张量。则卷积层中的每一个卷积核也都是具有?通道的三阶卷积核，故一层卷积层所包含的一组卷积核构成了形如? ×? ×? ×?的四阶张量。
基于张量分解的网络压缩的基本思想，就是利用张量分解的技术将网络的参数重新表达为小张量的组合。重新表达后的张量组一般能够在一定的精度下近似与原张量相同，而所占用的空间又得到大大降低，从而获得网络压缩的效果。文献[41]和文献[39]分别是利用张量CP分解和Tucker分解的网络压缩工作。文献[69]利用的是较新的TensorTrain分解方法，经过Tensor Train分解得到的张量组可以通过反向传播算法获得更新，实际上形成了一种占用空间更小的网络层。

[41] E. Denton, W. Zaremba, J. Bruna, et al. Exploiting Linear Structure Within Convolutional Networks for Efficient Evaluation[C]. Montreal, Quebec, Canada, 2014, 1269–1277

[39] Y. D. Kim, E. Park, S. J. Yoo, et al. Compression of deep convolutional neural networks for fast and low power mobile applications[J]. arXiv preprint arXiv:1511.06530, 2015

[69] A. Novikov, D. Podoprikhin, A. Osokin, et al. Tensorizing neural networks[C]. Neural Information Processing Systems, Montreal, Quebec, Canada, 2015, 442–450

2.2 基于量化的网络压缩

第二类网络压缩的方法是基于量化的方法。这里的量化主要包含两层含义,第一是用低精度参数代替高精度参数,对参数进行精度截取,其本质是均匀量化。第二是进行权重共享,限制网络权重可取的种类。有限的权重种类可以随后进行进一步编码,这种量化的手段本质是非均匀量化。
文献 [70] 是降低权重精度的一种极限情况,在该文献中,卷积网络的权重被二值化为+1与-1,网络的运算速度得到大幅度提升,存储消耗大幅度降低,且二值化网络有潜在的利用硬件逻辑运算实现的可能性。文献[46]是近期的权值共享的工作。权值共享的量化将网络权重的取值从全体实数集映射到有限数集的过程,在该工作中,每一层的网络权重被量化到{W n ,0,W p }三种可能的取值上,其中W p 和W n 在网络训练的过程中自适应的确定。

[70] M. Rastegari, V. Ordonez, J. Redmon, et al. XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks[C]. Amsterdam, The Netherlands, 2016

[46] C. Z. Zhu, S. Han, H. Z. Mao, et al.Trained Ternary Quantization[J].arXiv preprintarXiv:1612.01064, 2016

2.3 基于裁剪的网络压缩

基于张量分解和量化的网络压缩方法,其着眼点都是网络的参数。在网络压缩的过程中网络的拓扑结构保持不变。在基于裁剪的网络压缩中,网络的拓扑结构和数据的推断方法都可能发生改变。基于裁剪的网络压缩将直接改变网络的结构,其本质是将网络中的冗余部分剔除。
依据裁剪对象的不同,网络裁剪可以分为层级裁剪,神经元级裁剪,神经连接级裁剪等多个粒度。层级裁剪的裁剪对象是整个网络层,主要适合于网络层数较多的模型,裁剪的结果是神经网络变得更“浅” ,文献 [71] 去除了深度残差网络的若干模块,实际上就是一种层级裁剪。神经元级裁剪的裁剪对象是单个神经元或滤波器,裁剪的结果是神经网络变得更“瘦” 。神经连接级裁剪的目标是单个神经网络连接权,裁剪的结果是使得神经网络更“稀疏” 。图3-1(a)和图3-1(b)分布展示了神经元级裁剪与神经连接级裁剪的不同结果,一旦一个神经元被裁剪,则与它相连的所有连接权都被剪断。所以神经元裁剪实际上是神经连接裁剪的一种特殊情况。

[71] A. Veit, M. Wilber, S. Belongie. Residual Networks are Exponential Ensembles of Relatively Shallow Networks[J]. arXiv preprint:1605.06431, 2016

层级裁剪由于粒度较粗糙,对层内特征表达影响很大,研究相对较少。神经连接级裁剪是目前研究较多的网络压缩方法之一,相对而言具有更精细的裁剪粒度。但它具有的副作用是,稀疏的神经连接的保存需要使用稀疏张量的存储和运算方法。稀疏张量的存储需要保存数据点位置的额外存储开销,其实际节约的存储空间小于裁减掉的参数数目。稀疏张量的计算需要用特殊的计算方法,不利于并行计算。我们称神经连接级的裁剪破坏了网络的“正规性” 。神经元级裁剪是本文研究的主要内容,它的裁剪粒度适中,并且能够保持原网络的正规性。裁减后的网络是原网络的一个子网络,其运算方式、运行环境、并行方式不需要做任何更改。

2.4 神经网络冗余性分析与可视化

神经网络的冗余性是网络压缩的基础,只有存在冗余的神经网络才具有可压缩的空间。对神经元级的网络裁剪而言,我们所关心的是网络中神经元的功能是否重复。在本节中,我们提出一种称为特征图反转 [72] 的方式,并利用可视化的手段直观展示网络中滤波器的功能,随后通过图像聚类,直观展示神经网络中存在的滤波器功能重复现象。

[72] Z. Q. Xia, C. Zhu, Z. T. Wang, et al. Every Filter Extracts A Specific Texture In Convolutional Neural Networks[J]. arXiv preprint:1608.04170, 2016

2.5 神经网络可视化技术

神经网络的特点之一是可解释性弱,到目前为止,我们仍然缺乏关于神经网络工作原理的可靠解释。神经网络可视化技术是揭示神经网络工作原理,打开深度学习的“黑盒子”的一种方法。其主要目的是用可视化的手段直观展示神经网络中某一层、某一神经元的功能。神经网络的可视化主要包含激活值最大化 [73] 与编码反转 [74] 两种技术。设x是一张待优化的噪声图像,Φ l,i (x)是图像在l层第i个滤波器或神经元上的响应,则激活值最大法试图寻找图像x * 满足:

其中,R θ (x)是对图像的正则,包含了图像的先验信息,如TV范数。激活值最大化方法的过程就是不断强化一张初始图片,使其在感兴趣的神经元或网络层上有最大的响应。编码反转同样从一张初始图像x出发,设一张有意义图像在某一层或某一神经元上的响应为Φ 0 ,则编码反转不断优化初始图片,以满足:

其中l(Φ l,i (x), Φ 0 )是衡量输入图片特征与Φ 0 相似度的损失函数。编码反转通过寻找与目标图像具有相同特征的图像,揭示网络在解析目标图像时所做的工作。

[73] D. Erhan, Y. Bengio, A. Courville, et al. Visualizing higher-layer features of a deep network[J]. University of Montreal, 2009, 1341:3
[74] A. Mahendran, A. Vedaldi. Visualizing Deep Convolutional Neural Networks Using Natural Pre-images[J]. International Journal of Computer Vision, 2015, 5(4):1–23

2.6 特征图反转

我们在文献[72]中对编码反转做了改进,使得编码反转技术可以用于反应单个神经元的具体功能。对于含有C个卷积核的卷积层,图像x在该层的响应是形如H × W × C的三阶张量,沿着第三个维度的每一张2D特征图都对应于该卷积层中的一个滤波器,因而对单个特征图可视化的结果能够反应对应滤波器的功能。

在特征反转中,对于l层的给定的目标特征Φ l 0 ,我们选定感兴趣的滤波器i,然后修改目标特征Φ l 0 使得感兴趣滤波器所对应的特征图得到强化,而其他滤波器对应的特征图被弱化。具体而言,为了保持Φ l 0 的总能量不变,我们将感兴趣滤波器的响应强度设置为所有滤波器响应强度之和,并将其余滤波器的响应置为0。经过修正后,我们通过运行标准的特征图反转算法,即可得到反应感兴趣滤波器功能的图像。记Ψ(∙)为调整目标特征的操作,则Ψ(∙)定义为:

其中i是感兴趣滤波器。特征图反转的优化目标因而调整为:

算法的优化过程是标准的神经网络梯度反传过程,在前向运算中,x经神经网络在l层产生特征。在后向运算中,损失函数l()产生的梯度逐层反传,传入输入端的梯度对x进行调整。与一般的深度学习训练过程不同,在该过程中神经网络的参数保持固定不变,算法仅对输入图像进行修改。经过优化后产生的图像反映了目标神经元试图在内容图像中寻找的特征,经过分析,我们的结论是每一个滤波器都在试图从图像中寻找一类特定的纹理基元,利用纹理基元的相似性,我们可以直观的观察出神经元功能的重复性。我们将特征图反转的算法总结如算法1。