LeetCode 97. Interleaving String

题目：

Given s1, s2, s3, find whether s3 is formed by the interleaving of s1 and s2.

For example,
Given:
s1 = "aabcc",
s2 = "dbbca",

When s3 = "aadbbcbcac", return true.
When s3 = "aadbbbaccc", return false.

思路：递归求解，s3的每一个字符必定来自s1和s2其中一个。s3中的一个char既可以s1匹配和可以和s2匹配时，匹配一个后，匹配成功则返回，不然匹配另一个。进入递归。

其中，index1，index2，index3分别是s1,s2,s3指向将要匹配的char。递归会超时，最后一个case不能通过，应该循环能过。

class Solution {
public:
    bool iteatorleave(string s1, string s2, string s3,int index1,int index2,int index3)
    {
        if(index1==-1&&index2==-1&&index3==-1)
        {
            return true;
        }
        else
        {
            bool temp1=0,temp2=0;
            if(s1[index1]==s3[index3])
            {
                temp1=iteatorleave(s1,s2,s3,index1-1,index2,index3-1);
		if(temp1) return true;
            }
            if(s2[index2]==s3[index3])
            {
                temp2=iteatorleave(s1,s2,s3,index1,index2-1,index3-1);
		if(temp2) return true;
            }
             return false;
        }
    }
    bool isInterleave(string s1, string s2, string s3)
    {
        int len1=s1.size()-1,len2=s2.size()-1,len3=s3.size()-1;
        return iteatorleave(s1,s2,s3,len1,len2,len3);
    }
};

思路2：DP算法，建立二维的动态匹配地图，示例地图如下

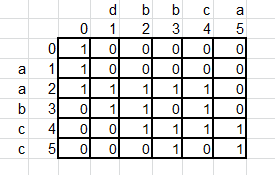
从左上走到右下即代表匹配成功，最后返回右下元元素（1代表能到达，0为不可到达），原地址：http://blog.csdn.net/doc_sgl/article/details/11714793 

没想过这种方法，记下。感觉应该可以用求直方图的最大矩形面积的动态规划栈的做法来实现，没继续思考。

class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        int m = s1.size();
        int n = s2.size();
        if(m+n != s3.size())
            return false;
        vector > path(m+1, vector(n+1, false));
        for(int i = 0; i < m+1; i ++)
        {
            for(int j = 0; j < n+1; j ++)
            {
                if(i == 0 && j == 0)
                // start
                    path[i][j] = true;
                else if(i == 0)
                    path[i][j] = path[i][j-1] & (s2[j-1]==s3[j-1]);
                else if(j == 0)
                    path[i][j] = path[i-1][j] & (s1[i-1]==s3[i-1]);
                else
                    path[i][j] = (path[i][j-1] & (s2[j-1]==s3[i+j-1])) || (path[i-1][j] & (s1[i-1]==s3[i+j-1]));
            }
        }
        return path[m][n];
    }
};