pandas DataFrame 空值和缺失值的处理;计算各特征的均值和方差;计算各自变量与目标变量的相关系数;计算各自变量(两两)之间的相关系数------未完!!!!!!
import numpy as np import pandas as pdfrom copy import deepcopy
pdf=pd.DataFrame([1,pd.NaT,3,"",np.nan],index=['int','NaT','int','null','nan'],columns=['列名']) print("type(pdf)-----------:",type(pdf)) print("pdf------------:") print(pdf)
#运行结果:
print(pdf.isnull())
#运行结果:
print(pdf[pdf==""])
#运行结果:
print(pdf["列名"][pdf["列名"]==""])
#运行结果:
df = pd.DataFrame([[np.nan, 2, np.nan, 0], [3, 4, "", 1],[np.nan, np.nan, np.nan, 5],[np.nan, 3, "", 4]], columns=list("ABCD"))print(df)
#运行结果:
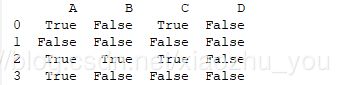
print(df.isnull())
#运行结果:
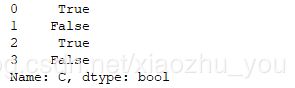
print(df['C'].isnull())
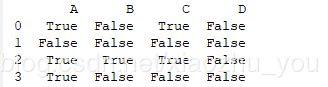
print(df.isna())
#运行结果:
print(df.dropna(inplace=False,axis=0))#备注:参数inplace=True时,操作的是原数据(即原DataFrame)
#运行结果:
print(df.dropna(inplace=False,axis=1))
#运行解果:
#填充空值。(步骤:先取再插)
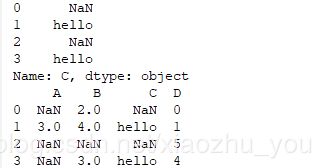
clean_z=df["C"] clean_z[clean_z==""]="hello" print(clean_z) df['C']=clean_z print(df)
#运行结果:
df = pd.DataFrame([[np.nan, 2, np.nan, 0], [3, 4, "", 1],[np.nan, np.nan, np.nan, 5],[np.nan, 3, "", 4]],
columns=list("ABCD"))print(df)
#运行结果:
clean=df["C"] print("type(clean)----------:",type(clean)) print("--"*20) print(clean[clean==""])
#运行结果:
print(df.mean(axis=1))#axis=1表示每行(抛却缺失值和空值)的均值
#运行解果:
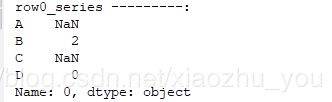
print("row0_series ---------:") print(row0_series)
#运行结果:
print("row0_series.isna()---:") print(row0_series.isna())
#运行结果:
print("row0_series[row0_series.isna()]--------:") print(row0_series[row0_series.isna()]) print("row0_series[row0_series.isna()==True]--:") print(row0_series[row0_series.isna()==True])
#运行结果:
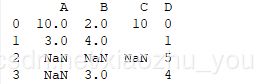
row0_series[row0_series.isna()]=10 #或:row0_series[row0_series.isna()==True]=10 df.loc[0,:]=row0_series print(df)
#运行结果:
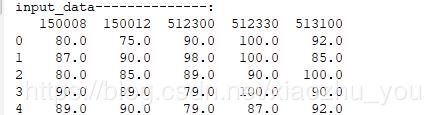
#读取文件 input_data=pd.read_csv('txt40.txt',header=0,dtype=np.float) print("input_data--------------:") print(input_data)
#运行结果:
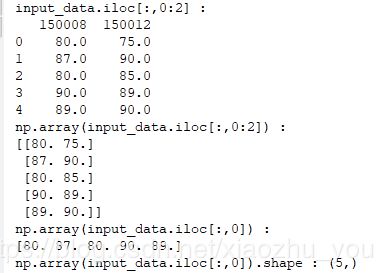
#pandas Series 和 pandas DataFrame 与numpy ndarray之间的关系 print("input_data.iloc[:,0:2] :") print(input_data.iloc[:,0:2]) print("np.array(input_data.iloc[:,0:2]) :") print(np.array(input_data.iloc[:,0:2])) print("np.array(input_data.iloc[:,0]) :") print(np.array(input_data.iloc[:,0])) print("np.array(input_data.iloc[:,0]).shape :",np.array(input_data.iloc[:,0]).shape)
#运行结果:
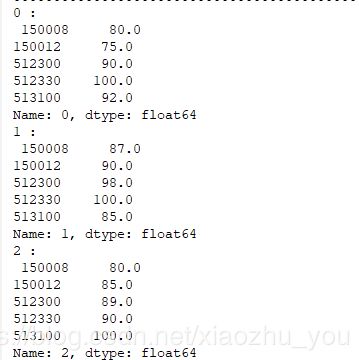
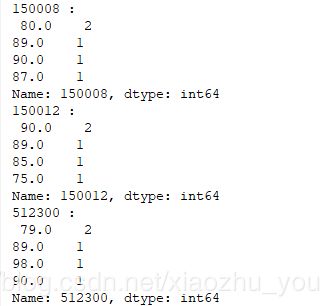
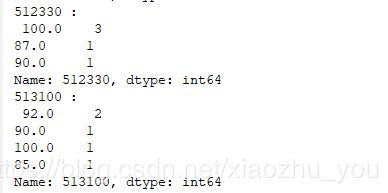
for index , row in input_data.iterrows():# row为DataFrame的一行数据, index为此行对应的索引。备注:row是pandas Series print(index,":\n",row) for column_name ,column in input_data.iteritems():# column为DataFrame的一列数据, column_name为此行列的列名。备注:column是pandas Series print(column_name,":\n",column.value_counts()) #Series().value_counts() //统计重复出现的数据的个数。返回以数据作为key,以重复次数为value的 Series对象。#input_data[0].value_counts().index[0] //最多的那个数
#运行结果:
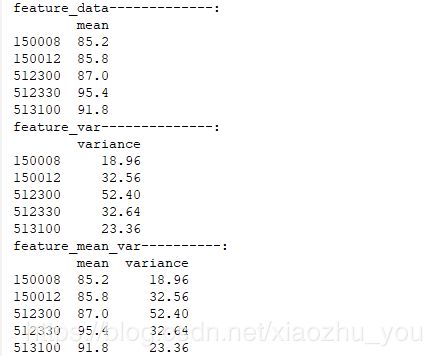
一. 计算各特征的均值和方差
def feature_mean_var(input_data): #3.计算各特征的均值和方差 #3.1计算各特征的均值 feature_mean=pd.DataFrame(np.mean(input_data,axis=0),index=input_data.columns,columns=["mean"]) print("feature_data-------------:") print(feature_mean) #3.2计算各特征的方差 feature_var=pd.DataFrame(np.var(input_data,axis=0),index=input_data.columns,columns=["variance"]) print("feature_var--------------:") print(feature_var) #3.3按照左右的index合并集合 feature_mean_var=pd.merge(feature_mean,feature_var,left_index=True,right_index=True) print("feature_mean_var----------:") print(feature_mean_var) feature_mean_var(input_data)
#运行结果:
二. z-score标准化
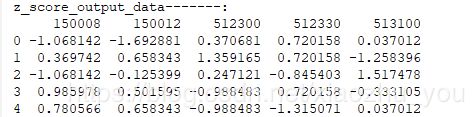
def z_score_scaler(input_data): #4. z-score标准化 公式:X=(X-X')/S # 备注:X--某特征向量;X'--此特征向量的均值;S--此特征向量的标准差。结果:此特征向量标准差为1,均值为0 #需要计算每个特征的均值和标准差 output_data=deepcopy(input_data) for i in range(input_data.shape[1]): col_data=output_data.iloc[:,i] mean_val=col_data.mean() #或则:mean_val=np.mean(col_data) std_val=col_data.std() if std_val !=0: output_data.iloc[:,i]=(col_data - mean_val)/std_val else: output_data.iloc[:,i]=0 return output_data output_data=z_score_scaler(input_data) print("z_score_output_data-------:") print(output_data)
#运行结果:
三. min-max标准化
def min_max_scaler(input_data):
#5. min-max标准化 公式:(X-X.min())/(X.max()-X.min())
#min-max为每一个特征向量的最小值和最大值,标准化之后的数据范围在[0,1]之间
output_data=np.ones_like(input_data)
for i in range(input_data.shape[1]):
col_data=input_data.iloc[:,i]
max_col=col_data.max()
min_col=col_data.min()
if max_col - min_col !=0:
output_data[:,i]=np.round((col_data - min_col)/(max_col - min_col),3)
else:
output_data[:, i]=0
return output_data
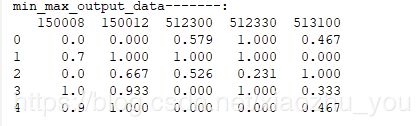
output_data=min_max_scaler(input_data)
output_data=pd.DataFrame(output_data,columns=input_data.columns)
print("min_max_output_data-------:")
print(output_data)#运行结果:
四. 正则化(normalization)
#将每个样本缩放到单位范数(每个样本的范数为1),如果后面要使用二次型(点积)或者其它核方法计算两个样本之间的相似性此方法会很有用。 #normalization的思想主要是对每个样本计算其p-范数,然后对该样本中的每个元素除以该范数,这样处理的结果是使得每个处理后的样本的p-范数 #等于1。p-范数计算公式:||X||p=(|x1|^p + |x2|^p +|x3|^p +...+ |xn|^p)^(1/p)备注:处理的每个样本。
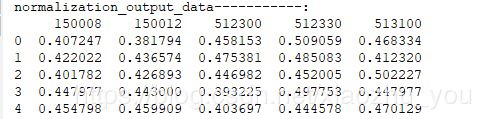
def normalization_data(input_data, norm_strategy): # 输入:需要处理的特征向量(为一个dataframe),处理的策略(l1(即p=1)或l2(即=2)范数) # 输出:经过正则处理后的dataframe output_data=deepcopy(input_data) for i in range(input_data.shape[0]): row_data=output_data.iloc[i,:] if norm_strategy=='l1': norm_val=row_data.map(abs).sum() #或者:norm_val=np.sum(row_data.apply(abs) # 注意:apply()和map()是Series的方法;而applymap()是pandas DataFrame的方法 output_data.iloc[i,:]=row_data/norm_val elif norm_strategy=="l2": norm_val=np.sqrt( (row_data.apply(lambda x:x**2).sum()) ) output_data.iloc[i,:]=row_data/norm_val else: return "参数norm_strategy传入有误!" return output_data output_data=normalization_data(input_data,'l2') print("normalization_output_data-----------:") print(output_data)
#运行结果:
五. 计算各自变量与目标变量(或因变量)的相关系数[借助皮尔森相关系数]
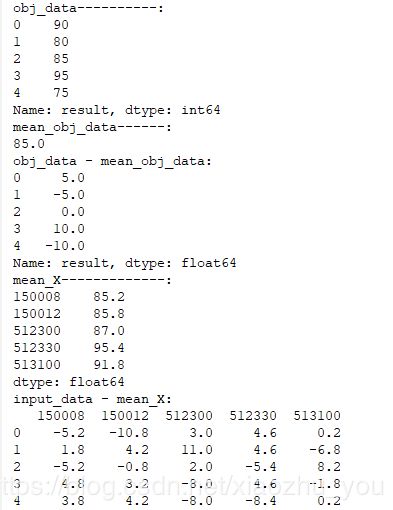
def cal_pearson(input_data, obj_data, sort_para): """ 计算各个特征和目标变量皮尔森相关系数,只能判断线性相关性,范围[-1,1]。 两个变量之间的皮尔逊相关系数定义为两个变量之间的协方差和标准差的商。 注释:0.8-1.0 极强相关 0.6-0.8 强相关 0.4-0.6 中等程度相关 0.2-0.4 弱相关 0.0-0.2 极弱相关或不相关 :param input_data: 特征向量的矩阵 :param obj_data: 目标变量 :param sort_para: 是否对输出进行排序 :return: pearson相关系数的数组,数组第i项为第i个特征的评分 """ print("obj_data----------:") print(obj_data) mean_obj_data=obj_data.mean() print("mean_obj_data------:") print(mean_obj_data) Y_deviation=obj_data - mean_obj_data print("obj_data - mean_obj_data:") print(Y_deviation)#目标变量(或因变量)的离差阵。(因为目标变量只有一个,所以是一个pandas Series) mean_X=input_data.mean(axis=0) #默认就是0轴。 print("mean_X-------------:") print(mean_X) X_deviation=input_data - mean_X #各随机变量的中与其对应的均值相减之后新生成的pandas DataFrame print("input_data - mean_X:") print(X_deviation)#各自变量的离差阵。(因为有多个变量,所以是一个pandas DataFrame) X_deviation_transpose=X_deviation.transpose()#转置 print("X_deviation_transpose:") print(X_deviation_transpose) dividend_pearson=X_deviation_transpose.dot(Y_deviation) #皮尔逊系数 分子部分 print("dividend_pearson------------:") print(dividend_pearson) divisor_pearson=np.sqrt((X_deviation**2).sum()) * np.sqrt((Y_deviation**2).sum()) #皮尔逊系数 分母部分 print("divisro_pearson-------------:") print(divisor_pearson) #各指标(或特征向量)皮尔逊系数 组成的Series对象如下: feature_pearson_coef=dividend_pearson*(divisor_pearson.map(lambda x:1/x)) #转换为DataFrame feature_pearson_coef=pd.DataFrame(feature_pearson_coef,index=input_data.columns,columns=['pearson_coef']) if sort_para==True: return feature_pearson_coef.sort_values(by=['pearson_coef'],ascending=False) else: return feature_pearson_coef obj_data=pd.Series([90,80,85,95,75],index=None,name='result') feature_pearson_coef=cal_pearson(input_data,obj_data,True) print("feature_pearson_coef------:") print(feature_pearson_coef)
#运行结果:
六. 计算各自变量(两两)之间的相关系数[借助皮尔森相关系数]
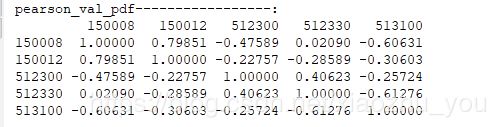
#第一种方法: def cal_pearson_feature(input_data): ''' 计算各个变量间的线性相关性使用pearson相关系数来评定。 一般输出两个系数:相关系数和检验系数p值,相关系数在[-1,1]之间,p值用来检验样本的显著水平; 如果不显著,相关系数再高也没用,可能只是因为偶然因素引起的。那么多少才算显著?一般p值小于0.05就是显著了;通常需要p值小于0.1, 最好小于小于0.05甚至0.01,才能得出结论:两组数据有明显关系;如果p=0.5,远大于0.1,只能说明相关程度不明显甚至不相关, 起码不是线性相关。 相关系数,也就是Pearson Correlation coefficent(皮尔逊相关系数),通常也称为R值。在确认上面指标显著情况下,再来看这个指标, 一般相关系数越高,表名两者关系越紧密。R>0表示两个变量正相关,即一个变大另一个也变大;R<0表示两个变量负相关,即一个变大但另一个变小; R=0比较特殊,这里暂不做分析。 :param input_data: 输入的的特征向量 :return: 各特征向量的相关矩阵的pandas DataFrame形式 ''' def pearson_correlation_coefficient(X,Y): ''' 求两个随机变量的皮尔逊相关系数 :param X: Series :param Y: Series :return: 各向量的相关矩阵的pandas DataFrame 注释:相关矩阵也叫相关系数矩阵,其是由矩阵各列间的相关系数构成的。 也就是说,相关矩阵第i行第j列的元素是原矩阵第i列和第j列的相关系数。 ''' mean_X=np.mean(X) deviation_X=X-mean_X mean_Y=np.mean(Y) deviation_Y=Y-mean_Y dividend_pearson=deviation_X.dot(deviation_Y) # print("dividend_pearson:",dividend_pearson) divisor_pearson=np.sqrt((deviation_X**2).sum())*np.sqrt((deviation_Y**2).sum()) pearson=dividend_pearson/divisor_pearson return pearson pearson_val=[] for i in range(input_data.shape[1]): for j in range(input_data.shape[1]): x= pearson_correlation_coefficient(input_data.iloc[:,i],input_data.iloc[:,j]) pearson_val.append(np.round(x,5)) return pd.DataFrame([pearson_val[5*k : 5*(k+1)] for k in range(len(pearson_val)//5)],index=input_data.columns, columns=input_data.columns) pearson_val_pdf=cal_pearson_feature(input_data) print("pearson_val_pdf-----------------:") print(pearson_val_pdf)
#运行结果:
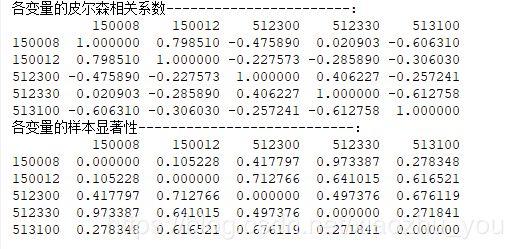
#第二种方法:借助scipy模块中的pearsonr函数方法实现,返回两变量的皮尔逊相关系数和样本显著性二元组。 def pearson_corr_coef(input_data): from scipy.stats import pearsonr pearson_correlation_pdf=pd.DataFrame([],index=input_data.columns,columns=input_data.columns) pearson_pvalue_pdf=pd.DataFrame([],index=input_data.columns,columns=input_data.columns) for i in range(input_data.shape[1]): for j in range(input_data.shape[1]): pearson_correlation_pdf.iloc[i,j] ,pearson_pvalue_pdf.iloc[i,j] = pearsonr(input_data.iloc[:,i],input_data.iloc[:,j]) # print("pearson_correlation_pdf:") # print(pearson_correlation_pdf) # print("pearson_pvalue_pdf:") # print(pearson_pvalue_pdf) return pearson_correlation_pdf, pearson_pvalue_pdf print("各变量的皮尔森相关系数-----------------------:") print(pearson_corr_coef(input_data)[0].astype(dtype='float')) print("各变量的样本显著性---------------------------:") print(pearson_corr_coef(input_data)[1].astype(dtype='float'))
#运行结果:
'''
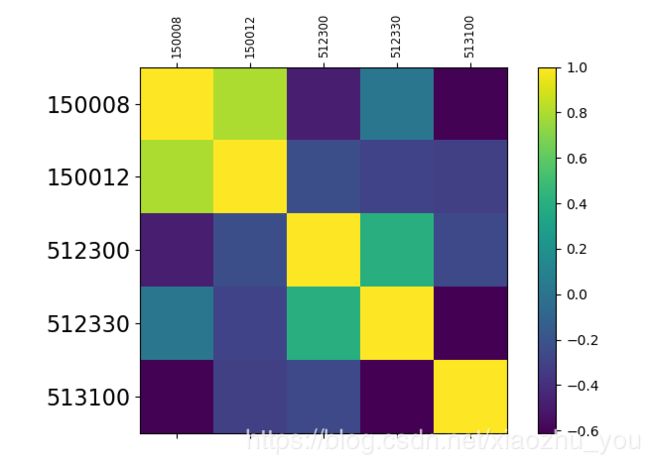
画出皮尔逊相关系数的"矩阵图"
'''
import matplotlib.pyplot as plt
def plot_pearson_coef(input_data):
pearson_cor, p_value=pearson_corr_coef(input_data)#这是上面自定义的方法
fig=plt.figure()
fig.set_size_inches(8,5)
ax=fig.add_subplot(111)
cax=ax.matshow(pearson_cor.astype(dtype='float'))#绘制热力图,从-1到1
# print("cax-----------:",cax)#AxesImage(100,55;620x385)
fig.colorbar(cax)#为matshow生成的热力图设置颜色渐变条
ticks=np.arange(0,len(input_data.columns),1)
ax.set_xticks(ticks=ticks)#生成刻度
ax.set_yticks(ticks=ticks)#生成刻度
ax.set_xticklabels(labels=input_data.columns,rotation=90,fontdict={"fontsize":'small'})#生成x轴标签
ax.set_yticklabels(labels=input_data.columns,fontdict={"fontsize":16})#生成y轴标签
plt.show()
plot_pearson_coef(input_data)
#运行结果:
七. 计算输入的samples中与变量A有最大相关性的变量B,以及它们的p值(即显著相关性)
def max_pearson_corr(input_data, *val_thre):
'''
计算输入的samples中与变量A有最大相关性的变量B,以及他们的p值。
:param input_data: 需要计算的特征向量数据(dataframe格式)
:param val_thre: 相关系数的阈值
:return: 相关系数最大的向量
'''
pearson_cor, p_value = pearson_corr_coef(input_data)#上文中自定义的函数
lis=[] #或 lis1=[]
for i in range(pearson_cor.shape[1]):
sorted_coef=pearson_cor.iloc[:,i].sort_values(ascending=False)
max_coef_val=sorted_coef.values[1]
max_coef_name=sorted_coef.index[1]
pvalue=p_value.loc[max_coef_name,sorted_coef.name]
pvalue1=p_value.loc[sorted_coef.name,max_coef_name]
lis.append([sorted_coef.name,max_coef_name,max_coef_val,pvalue])
#或:lis1.append([sorted_coef.name,max_coef_name,max_coef_val,pvalue1])
max_coef_pdf=pd.DataFrame(lis,columns=["variable_initial","variable_correlation",'max_coef',"pvalue"])
#或:max_coef_pdf1=pd.DataFrame(lis1,columns=["variable_initial","variable_correlation",'max_coef',"pvalue"])
return max_coef_pdf #或 return max_coef_pdf1
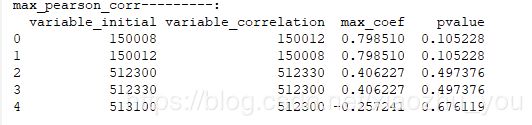
max_pearson_corr=max_pearson_corr(input_data)
print("max_pearson_corr---------:")
print(max_pearson_corr)#运行结果: