MLX90640开发笔记(五)阵列插值处理-多项式插值由32*24像素到512*384像素
MLX90640的32*24=768像素虽然比以往的8*8或者16*8像素提高了很多,但若直接用这些像素还是不能很好的形成热像图,为了使用这些像素点平滑成像就需要对其进行插值,使用更多的像素来绘制图像。
看了一些别人的算法,感觉主要就是多项式插值,仅是插值方法的组合方式不同。
比较有代表性的是杭州电子科技大学杨风健等《基于MLX90620的低成本红外热成像系统设计》,使用三次多项式+双线性插值,将原16*4像素扩展为256*64像素。双线性插值的本质就是一次函数(一次多项式)。该文章得到的结论是:
(1)双线性插值法计算量小、速度快,但对比度低、细节模糊。
(2)三次多项式插值,图像效果较清晰,对比度较高,但计算量较大。
(3)先双线性插值再三次多项式插值,效果优于上两种单一插值方法。
(4)先三次多项式插值再双线性插值,高低温分布更加明显,图像效果更接趋于真实。
同时,该文章还使用了一种对图像质量的评估方法---熵&平均梯度
熵,热力学中表征物质状态的参量之一,用符号S表示,其物理意义是体系混乱程度的度量。用于图像评价表示图像表达信息量的多少。图像熵越高信息量越大。
平均梯度,指图像的边界或影线两侧附近灰度有明显差异,即灰度变化率大,这种变化率的大小可用来表示图像清晰度。它反映了图像微小细节反差变化的速率,即图像多维方向上密度变化的速率,表征图像的相对清晰程度。值越大表示图像越清晰。
插值实现
每行或者列的首个像素在前面插值2个点
1~n-1像素,每个像素后面插值3个点
最后一个像素,在后面插值1个点
n+2+(n-1)*3+1=n+2+n*3-1*3+1=4n+2-3+1=4n,即:像素变为原来的4倍
上面的处理方法,首个像素之前插入2个点,最后一个像素之后插入1个点,下次插值时,应首个之前插值1个点,末个像素之后插值2个点,以达到图像平衡。
每次插值后像素为插值前的4倍,经过两次插值,即可将32*24改变为512*384像素。
下面是已经实际使用的插值算法,不过是用Pascal(Delphi)写的,有兴趣的可以改为C语言的,语句对应直接改就行,语言本来就是相通的嘛。
//这是一维数组插值算法
//SourceDatas:TDoubles;插值前的一维数组
//Dir:Integer;在哪个方向和末尾插入2个值(0:前面;1:末尾)
//times:Integer多项式的项数,一次多项式是2项,二次多项式是3项
//返回值:插值后的一维数组(数量是插值前*4)
function PolynomialInterpolationArr(
SourceDatas:TDoubles;
Dir:Integer;
times:Integer):TDoubles;//一维数组插值
var
i,j,k:Integer;
arrCount:Integer;
startIndex:Integer;
OriginDatas,TargetDatas:ArrayOf2D;
tempStr:string;
tempDou:Double;
coes:array[0..5] of Double;
begin
arrCount:=Length(SourceDatas);
SetLength(Result,arrCount*4);
if Dir=0 then startIndex:=2
else startIndex:=1;
//源数据复制到目标数组Result
for i := 0 to arrCount-1 do
begin
Result[startIndex+i*4]:=SourceDatas[i];
end;
SetLength(OriginDatas,2,times);
//插值,插值完成后是*4像素
for i := 0 to arrCount-times do
begin
for j := 0 to times-1 do//初始化拟合原始数据
begin
OriginDatas[0][j]:=j*4;
OriginDatas[1][j]:=SourceDatas[i+j];
end;
GetPolyData_U(OriginDatas,times,coes);
//插值
for j := 1 to 4-1 do
begin
if times>=2 then tempDou:=coes[0]+j*coes[1];
if times>=3 then tempDou:=tempDou+j*j*coes[2];
if times>=4 then tempDou:=tempDou+j*j*j*coes[3];
Result[startIndex+i*4+j]:=tempDou;
end;
end;
//两端插值,两端插值直接使用线性插值(一次多项式)
SetLength(OriginDatas,2,2);
//前端插值
OriginDatas[0][0]:=0;
OriginDatas[1][0]:=SourceDatas[0];
OriginDatas[0][1]:=4;
OriginDatas[1][1]:=SourceDatas[1];
GetPolyData_U(OriginDatas,2,coes);
if Dir=0 then
begin
tempDou:=coes[0]+(-1)*coes[1];
Result[1]:=tempDou;
tempDou:=coes[0]+(-2)*coes[1];
Result[0]:=tempDou;
end
else
begin
tempDou:=coes[0]+(-1)*coes[1];
Result[0]:=tempDou;
end;
//末端插值
for i := (arrCount-times) to (arrCount-2) do
begin
for j := 0 to 2-1 do//初始化拟合原始数据
begin
OriginDatas[0][j]:=j*4;
OriginDatas[1][j]:=SourceDatas[i+j];
end;
GetPolyData_U(OriginDatas,2,coes);
//插值
for j := 1 to 4-1 do
begin
tempDou:=coes[0]+j*coes[1];
Result[startIndex+i*4+j]:=tempDou;
end;
end;
if Dir=0 then
begin
tempDou:=coes[0]+(5)*coes[1];
Result[arrCount*4-1]:=tempDou;
end
else
begin
tempDou:=coes[0]+(5)*coes[1];
Result[arrCount*4-2]:=tempDou;
tempDou:=coes[0]+(6)*coes[1];
Result[arrCount*4-1]:=tempDou;
end;
end;
上面函数里用到的一个系数求解函数如下
function GetPolyData_U(OriginData: ArrayOf2D;times:Integer;var coes:array of Double): ArrayOf2D;//times为项数,1次多项式有ab两项,以些类推
var
x1,x2,x3,x4:Double;
y1,y2,y3,y4:Double;
begin
//1次多项式:a+bx=y
//2次多项式:a+bx+cx^2=y
//3次多项式:a+bx+cx^2+dx^3=y
if ((times<2) or (times>4)) then
times:=2;
if times=2 then
begin
x1:=OriginData[0][0];
x2:=OriginData[0][1];
y1:=OriginData[1][0];
y2:=OriginData[1][1];
coes[1]:=(y2-y1)/x2;
coes[0]:=y1;
end
else if times=3 then
begin
x1:=OriginData[0][0];
x2:=OriginData[0][1];
x3:=OriginData[0][2];
y1:=OriginData[1][0];
y2:=OriginData[1][1];
y3:=OriginData[1][2];
coes[2]:=((y3-y1)*x2-(y2-y1)*x3)/(x2*x3*x3-x2*x2*x3);
coes[1]:=(y2-y1)/x2-coes[2]*x2;
coes[0]:=y1;
end
else if times=4 then
begin
x1:=OriginData[0][0];
x2:=OriginData[0][1];
x3:=OriginData[0][2];
x4:=OriginData[0][3];
y1:=OriginData[1][0];
y2:=OriginData[1][1];
y3:=OriginData[1][2];
y4:=OriginData[1][3];
coes[3]:=((y4-y1)*x2-(y2-y1)*x4)/x2-((y3-y1)*x2-(y2-y1)*x3)/(x2*x3*x3-x2*x2*x3)*(x2*x4*x4-x2*x2*x4)/x2;
coes[3]:=coes[3]/((x2*x4*x4*x4-x2*x2*x2*x4)/x2-(x2*x3*x3*x3-x2*x2*x2*x3)/(x2*x3*x3-x2*x2*x3)*(x2*x4*x4-x2*x2*x4)/x2);
coes[2]:=((y3-y1)*x2-(y2-y1)*x3)/(x2*x3*x3-x2*x2*x3)-coes[3]*((x2*x3*x3*x3-x2*x2*x2*x3)/(x2*x3*x3-x2*x2*x3));
coes[1]:=((y2-y1)-coes[2]*x2*x2-coes[3]*x2*x2*x2)/x2;
coes[0]:=y1;
end;
end;
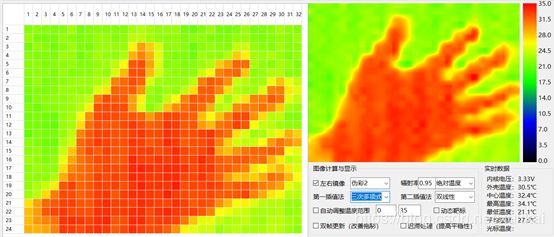
下面是几个效果图
我并没有体会到文章开始时提到的那篇论文所说的“先三次多项式插值再双线性插值,高低温分布更加明显,图像效果更接趋于真实”
MLX90640开发笔记(一)概述及开发资料准备
MLX90640开发笔记(二)API移植-I2C和关键接口函数
MLX90640开发笔记(三)工作流程和操作MLX90640的一般步骤
MLX90640开发笔记(四)损坏和不良像素的处理
MLX90640开发笔记(五)阵列插值处理-多项式插值由32*24像素到512*384像素
MLX90640开发笔记(六)红外图像伪彩色编码
MLX90640开发笔记(七)小结-注意事项
MLX90640开发笔记(八)扩展知识-辐射率、灵敏度、精度、探测距离
MLX90640开发笔记(九)EEPROM、RAM、寄存器说明
MLX90640开发笔记(十)成果展示-红眼睛相机