线性代数:理解矩阵的作用
现在我们正式进入矩阵的学习了,矩阵Matrix这个词我相信小伙伴们第一次接触,基本就是在小时候看黑客帝国的时候,黑客帝国中有个经典的场景,就是数字世界在解放后的尼奥双眼中已经变成了一串串数字瀑布流,就是下面:
一串串的数字流组成了一个“数字集合矩形块”,这个大概就是我们小时候不知不觉接触的矩阵原型了。
我们再来看下数学中的矩阵写法,如下图:
咋一看矩阵就是一个三行三列的数字集合。当然我们也可以写一个两行两列,或者四行四列,这些也是矩阵,那么我们可以说矩阵就是m行n列的数字集合,当然了假如m = 1或者n = 1,那么矩阵就变成一个向量?如下图:
这么一看,向量和矩阵就没啥区别,或者说向量就是矩阵的一种特殊形式,反过来说矩阵也可以看成一组向量的集合,比如上图的左边三组竖着的向量或者右边三组横着的向量的组合就变成一个矩阵。
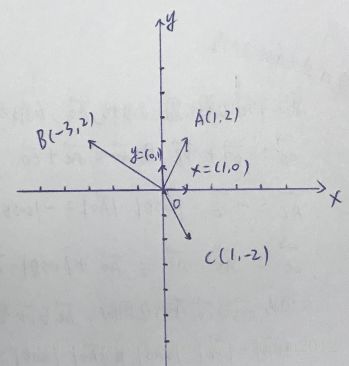
这个时候我们就把矩阵的形式转换成为向量组的形式了,接下来我们看下“向量组”到底是个什么东西。从最简单的二维向量组来,比如我们定义一堆二维向量A = {1,2} B = {-3,2} C = {1,-2},X = {1,0} ,Y = {0,1}然后我们在xy坐标系中描绘一下,如下图:
如果我们观察,会发现其实A = X+2Y,B = -3X + 2Y,C = X + -2Y,这么一看其实xy平面上的向量其实都可以用X,Y这种模长等于1且与X轴Y轴重合的基向量表示,则m*X+n*Y = K,K为平面xy上任意一个向量,我们继续转换一下,因为ABC已经用X,Y基向量表示了,那么ABC随意转换一下就能互相表示了,比如B = -A + -2C,此时我们就抛开了XY基坐标直接表示B向量了,所以说,m*A + n*C = B就能理解成,平面内两个向量与两个任意数值就能表示任意第三个向量,那么说m*A + n*C能张成一张平面,如下图:
假如m,n>0则张成的类似上图的平面,假如m,n为任意值那就是xy整个平面了。
二维的向量组的含义就在于此,那就是可以通过数值代入计算得到第三个向量,比如:
β = m*α1 + n*α2
数学称β可以由向量组{α1,α2}线性表示,同时称β,α1,α2为线性相关。
ps:反过来就是说假如β不能由{α1,α2}线性表示,则称β,α1,α2为线性无关。
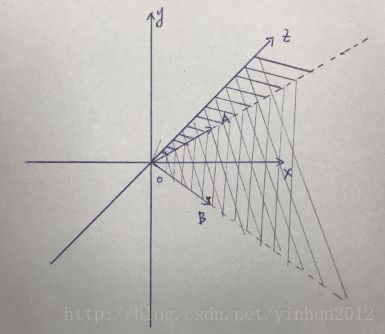
接下来我们来看看三维向量组的意义,通过上面的二维向量组“张成平面的能力“,我们进行z轴扩充,会发现三维向量组能够”张成“一个立体空间,如下图:
在OA,OB,OZ张成的立体空间中任意向量β = m*OA + n*OB + k*OZ(m,n,k>0),β就是{OA,OB,OZ}的线性表示,当然假如m,n,k为任意实数,就是”张成“了xyz的全部空间了。
这里就有个名词蹦出来了,就是子空间,假如我们把上面m,n,k为任意实数构成的空间叫做S,那么m,n,k>0构成的空间S1就是S的一个子空间。
说道这里,总结一下:一个向量组{α1,α2,α3....αn},这个向量组的所有线性组合生成一个向量合集:
{x1*α1 + x2*α2 + x3*α3 ...+xn*αn }且x1,x2...xn属于R
这个向量集合称为Span{α1,α2,α3....αn},称为向量组{α1,α2,α3....αn}张成的向量空间。
与此同时,数学上又给了一些定义:
对于向量空间S中的一个有序向量组{α1,α2,α3....αn},假如α1,α2,α3....αn线性无关,且任意向量β = x1*α1 + x2*α2 + x3*α3 ...+xn*αn
那么我们称向量组{α1,α2,α3....αn}为向量空间S的一个基,向量组的向量个数称为S的维数,有序实数组{x1,x2,x3...xn}为向量β在基{α1,α2,α3....αn}上的坐标。
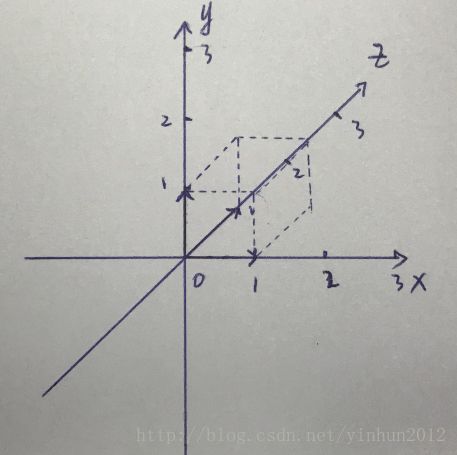
基的作用很重要,我们给一个向量空间Space找一个基,目的就是给这个空间定义一个参考坐标系,以便我们定位向量,同时进行向量运算。那么我们可以理解为,选取一个基其实就是选取了一个参考坐标系,选取另一个基就是选取了另一个参考坐标系,当我们从某个基(参考坐标系)来观察,那么基中的向量就是参考坐标系的坐标轴,一组基中有几个基向量就是几个坐标轴,n维空间的一个基就需要n个基向量,当然了我们学习图形学只是研究三维空间就是了,如下图:
上面说过建立坐标系的目的就是把空间向量的线性变换转换为坐标数值的运算:在空间中选取一点做为O原点,从O为起点做任意三个不共面的向量α1,α2,α3,这种方式建立的坐标系叫做仿射坐标系,写成:{O;α1,α2,α3},那么任意一个向量α可以用实数组(x,y,z)来表示,既:α = x*α1+y*α2+z*α3,这里我们称(x,y,z)为向量α的坐标。
ps:仿射坐标系右分为左手和右手坐标系,具体纸面上的区别就是z轴朝纸面内还是纸面外,如果用手来表示就是食指中指拇指成90度夹角,食指朝x轴,中指朝y轴,那么大拇指和z轴的朝向就是区分左右手了。
重要的来了,我们来学习基变换。
假设一个n维线性空间Space中选取两组基{α1,α2,α3....αn}和{β1,β2,β3...βn},如果我们使用基{α1,α2,α3....αn}当作线性空间的坐标系,那么基{β1,β2,β3...βn}怎么用基{α1,α2,α3....αn}来表示呢?
这里我们依次来看,因为基{β1,β2,β3...βn}中任意一个向量都能用基{α1,α2,α3....αn}来表示:
β1 = m11*α1 + m12*α2 + m13*α3 + ... + m1n*αn
β2 = m21*α1 + m22*α2 + m23*α3 + ... + m2n*αn
β3 = m31*α1 + m32*α2 + m33*α3 + ... + m3n*αn
...
βn = mn1*α1 + mn2*α2 + mn3*α3 + ... + mnn*αn
看出来一点什么么?如下图:
上图的写法是一种数学规定,其实就是为了记录方便,主要就是矩阵A行*矩阵B列中各个对应元素相乘然后相加(是不是感觉有点类似点积),得到的结果矩阵C在矩阵左乘情况下,行数等于矩阵A的行数,C列数等于矩阵B的列数。这里我们化出参数K,如下图:
如果我们已经规定了行*列的计算法,那么其实向量左乘和右乘其实是不同的参数K,这也是就是矩阵的乘法需要注意的地方。
K这个参数就变成了有行有列的数值的集合,回想一下黑客帝国,是不是已经很像了,这个K我们称为矩阵。
同时我们对K1和K2有个关联的定义,就是互称转置矩阵,观察会发现K1的行和K2的列刚好相同,我们说K1是K2的转置矩阵(K2也是K1的转置矩阵)。
这个时候就是矩阵的作用就正式揭开了,就是向量变换,矩阵可以把一个向量变换成另外一个向量。
我们来想象一下,科幻电影中,一艘太空战舰正在太空中慢慢遨游着,突然舰长发出消息,有个任务要本舰立刻到达α星球进行虫族的战斗,于是战舰开启超光速引擎,一瞬间就”跃迁“到α星球附近的太空中,矩阵的作用就和这个类似,就是把向量A”跃迁“成向量B。
ps:矩阵乘法的这种方式在经济学上也有应用,打个比方,超市中面包一个3.5元,鸡蛋一个1元,冰淇淋一个5元,假如我们买2个面包,4个鸡蛋,1个冰淇淋,那么我们花的钱就是3.5*2+1*4+5*1 = 16元,假如我们写成矩阵乘法形式,如下图:
顺便聊一下,1973年诺贝尔经济学奖得主华西里·列昂惕夫的投入产出线性方程组中,其设定了37个未知数的线性方程,也是矩阵应用的一种。
顺便说一下,我们选择当作参考坐标系的基都会使用标准正交基,标准正交基就是基向量两两垂直模长等于1,这个应该很好理解,因为我们学习的时候基本都是用标准正交基做计算。
矩阵的计算中,行和列的处理方法(也就是行的元素一次*列的元素然后相加)展开后就变成了一个线性方程组,我们也可以说解矩阵(或者说解矩阵中未知数)就是解一个线性方程组。