机器学习中的评价指标(分类指标评Accuracy、Precision、Recall、F1-score、ROC、AUC )(回归指标评价MSE、RMSE、MAE、MAPE、R Squared)
文章目录
- 1.机器学习中的评价指标
- 基础
- (一)分类指标评价
- 1.Accuracy
- 2.Precision、查准率
- 3.Recall、查全率
- 4.F1-score
- 举个例子:
- 5.ROC
- 6.AUC
- (二)回归指标评价
- 1.均方误差(MSE)
- 2.均方根误差(RMSE)
- 3.MAE(平均绝对误差)
- 4.MAPE
- 5.R Squared
1.机器学习中的评价指标
简要介绍精度、精确率、召回率、P-R曲线、F1 值、TPR、FPR、ROC、AUC等指标
基础
(一)分类指标评价
在分类任务中,各指标的计算基础都来自于对正负样本的分类结果,用混淆矩阵表示为:

from sklearn.metrics import confusion_matrix
y_pred = [0,1,0,1]
y_true = [0,1,1,1]
confusion_matrix(y_true, y_pred, labels=[1, 0])
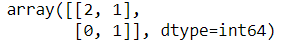
下面的表中P或者N都是代表了为预测出来的分类,分别代表了正类和负类,然后T或者F就代表了样本实际的分类与预测是一样的还是不一样的,我觉得这样去理解,应该就不会混了。
精度
1.Accuracy
定义:(TP+TN)/(TP+FN+FP+TN)
即所有分类正确的样本占全部样本的比例
## accuracy
import numpy as np
from sklearn.metrics import accuracy_score
y_pred = [0,1,0,1]
y_true = [0,1,1,1]
print('ACC:',accuracy_score(y_true,y_pred))
![]()
精确率
2.Precision、查准率
定义:(TP)/(TP+FP)
即预测是正例的结果中,确实是正例的比例
分母为预测为正样例的个数 ;分子为预测为实际正样例被预测准的个数
from sklearn import metrics
y_pred = [0,1,0,1]
y_true = [0,1,1,1]
print('Precision',metrics.precision_score(y_true,y_pred))
![]()
召回率
3.Recall、查全率
定义:(TP)/(TP+FN)
即所有正例的样本中,被找出的比例
分母为实际正样例的个数;分子为预测为实际正样例被预测准的个数
from sklearn import metrics
y_pred = [0,1,0,1]
y_true = [0,1,1,1]
print('Recall',metrics.recall_score(y_true,y_pred))
![]()
4.F1-score
from sklearn import metrics
y_pred = [0,1,0,1]
y_true = [0,1,1,1]
print('F1-score:',metrics.f1_score(y_true, y_pred))
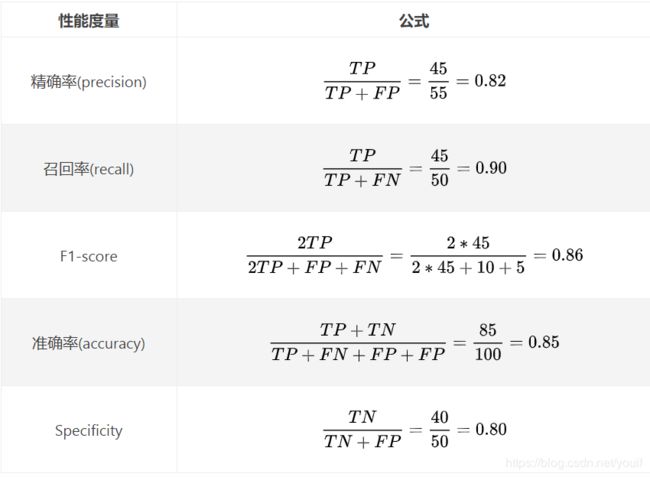
举个例子:
我们实际有50个样例,50个负样例,然后经过分类器分类之后。50个正样例中有45个预测为正样例(预测准了),5个被预测成为了负样例。50个负样例中(预测错误),有40个被预测为了负样例(预测准了),10个被预测为了正样例(预测错误)。

根据这个例子,我们可以计算出:
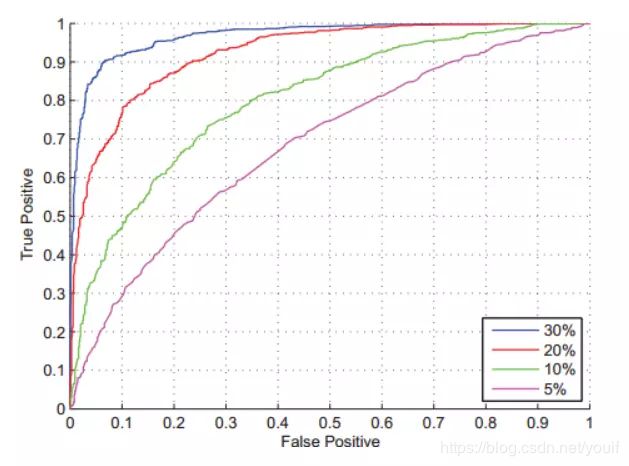
5.ROC
受试者工作特征
定义:根据预测结果将预测样本排序,最有可能为正样本的在前,最不可能的在后,依次将样本预测为正样本,分别计算当前的TPR和FPR,绘制ROC曲线。
6.AUC
Area Under ROC Curve
定义:ROC曲线下的面积
## AUC
import numpy as np
from sklearn.metrics import roc_auc_score
y_true = np.array([0, 0, 1, 1])
y_scores = np.array([0.1, 0.4, 0.35, 0.8])
print('AUC socre:',roc_auc_score(y_true, y_scores))
![]()
(二)回归指标评价
分类问题的评价指标是准确率,那么回归算法的评价指标就是MSE,RMSE,MAE、R-Squared。下面一一介绍
1.均方误差(MSE)
MSE (Mean Squared Error)叫做均方误差。看公式

这里的y是测试集上的。
用 真实值-预测值 然后平方之后求和平均。
猛着看一下这个公式是不是觉得眼熟,这不就是线性回归的损失函数嘛!!! 对,在线性回归的时候我们的目的就是让这个损失函数最小。那么模型做出来了,我们把损失函数丢到测试集上去看看损失值不就好了嘛。简单直观暴力!
# coding=utf-8
import numpy as np
from sklearn import metrics
y_true = np.array([1.0, 5.0, 4.0, 3.0, 2.0, 5.0, -3.0])
y_pred = np.array([1.0, 4.5, 3.8, 3.2, 3.0, 4.8, -2.2])
# MSE
print('MSE:',metrics.mean_squared_error(y_true, y_pred))
![]()
源码:
y_preditc=reg.predict(x_test) #reg是训练好的模型
mse_test=np.sum((y_preditc-y_test)**2)/len(y_test) #跟数学公式一样的
2.均方根误差(RMSE)
RMSE(Root Mean Squard Error)均方根误差。
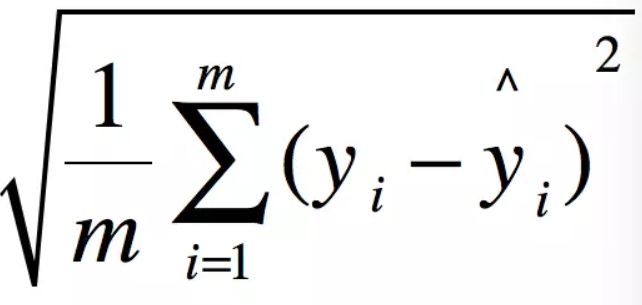
这不就是MSE开个根号么。有意义么?其实实质是一样的。只不过用于数据更好的描述。
例如:要做房价预测,每平方是万元(真贵),我们预测结果也是万元。那么差值的平方单位应该是 千万级别的。那我们不太好描述自己做的模型效果。怎么说呢?我们的模型误差是 多少千万?。。。。。。于是干脆就开个根号就好了。我们误差的结果就跟我们数据是一个级别的可,在描述模型的时候就说,我们模型的误差是多少万元。
import numpy as np
from sklearn import metrics
y_true = np.array([1.0, 5.0, 4.0, 3.0, 2.0, 5.0, -3.0])
y_pred = np.array([1.0, 4.5, 3.8, 3.2, 3.0, 4.8, -2.2])
# RMSE
print('RMSE:',np.sqrt(metrics.mean_squared_error(y_true, y_pred)))
![]()
源码:
rmse_test=mse_test ** 0.5
MAE
3.MAE(平均绝对误差)
import numpy as np
from sklearn import metrics
y_true = np.array([1.0, 5.0, 4.0, 3.0, 2.0, 5.0, -3.0])
y_pred = np.array([1.0, 4.5, 3.8, 3.2, 3.0, 4.8, -2.2])
# MAE
print('MAE:',metrics.mean_absolute_error(y_true, y_pred))
![]()
源码:
mae_test=np.sum(np.absolute(y_preditc-y_test))/len(y_test)
4.MAPE
平均绝对百分比误差(Mean Absolute Percentage Error)
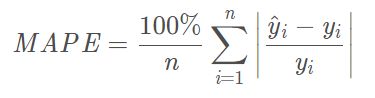
范围[0,+∞),MAPE 为0%表示完美模型,MAPE 大于 100 %则表示劣质模型。
可以看到,MAPE跟MAE很像,就是多了个分母。
注意点:当真实值有数据等于0时,存在分母0除问题,该公式不可用!
import numpy as np
from sklearn import metrics
# MAPE需要自己实现
def mape(y_true, y_pred):
return np.mean(np.abs((y_pred - y_true) / y_true))
y_true = np.array([1.0, 5.0, 4.0, 3.0, 2.0, 5.0, -3.0])
y_pred = np.array([1.0, 4.5, 3.8, 3.2, 3.0, 4.8, -2.2])
# MAPE
print('MAPE:',mape(y_true, y_pred))
![]()
5.R Squared
上面的几种衡量标准针对不同的模型会有不同的值。比如说预测房价 那么误差单位就是万元。数子可能是3,4,5之类的。那么预测身高就可能是0.1,0.6之类的。没有什么可读性,到底多少才算好呢?不知道,那要根据模型的应用场景来。
看看分类算法的衡量标准就是正确率,而正确率又在0~1之间,最高百分之百。最低0。很直观,而且不同模型一样的。那么线性回归有没有这样的衡量标准呢?答案是有的。
那就是R Squared也就R方

懵逼(X2)
慢慢解释。其实这个很简单。
上面分子就是我们训练出的模型预测的所有误差。
下面分母就是不管什么我们猜的结果就是y的平均数。(瞎猜的误差)
那结果就来了。
如果结果是0,就说明我们的模型跟瞎猜差不多。
如果结果是1。就说明我们模型无错误。
如果结果是0-1之间的数,就是我们模型的好坏程度。
如果结果是负数。说明我们的模型还不如瞎猜。(其实导致这种情况说明我们的数据其实没有啥线性关系)
## R2-score
from sklearn.metrics import r2_score
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
print('R2-score:',r2_score(y_true, y_pred))
![]()
源码:
1- mean_squared_error(y_test,y_preditc)/ np.var(y_test)
有些地方回顾不到位,请指教了哈!喜欢的小伙伴就给点个赞吧。
所有巧合的是要么是上天注定要么是一个人偷偷的在努力。
公众号
专注于学习资源、笔记分享,欢迎关注。我们一起成长,一起学习。一直纯真着,善良着,温情地热爱生活,,如果觉得有点用的话,请不要吝啬你手中点赞的权力,谢谢我亲爱的读者朋友。
![]()
It’s never too late to start over,Even at 3 a.m. on a Saturday,It can also be a new starting point for you。Einstein said:“Time is an illusion.”
重新开始永远都不晚,就算是周六的凌晨3点,也可以成为你新的起点。爱因斯坦说了:“时间是一种幻觉”
2020年4月12日于重庆城口
好好学习,天天向上,终有所获

