算法背后的数学原理
任何一种互联网大数据算法背后都有数学原理在支撑,无论是简单的递归迭代或者是更复杂的加密算法,都离不开数学原理,为了更好地方便大家理解,我们以加密算法为例,更好地阐述一下数学对算法的支持。
1、对称加密算法AES
AES 是 Advanced Encryption Standard 的缩写,是最常见的对称加密算法。AES 在密码学中又称 Rijndael 加密法,是美国联邦政府采用的一种区块加密标准。这个标准已经被多方分析且广为全世界所使用。
AES 的加密公式为 C=E(K,P),其中K 为密钥,P 为明文,C 为密文。
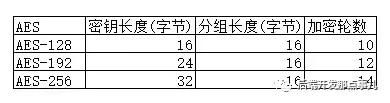
AES 加密明文的过程是:首先对明文进行分组,每组的长度都是 128 位,然后一组一组地加密,直到所有明文都已加密。密钥的长度可以是 128、192 或 256 位。
在加密函数 E 中,会执行一个轮函数,除最后一次执行不同外,前面几轮的执行是相同的。以 AES-128 为例,推荐加密轮数为 10 轮,即前 9 轮执行的操作相同,第 10 轮执行的操作与前面不同。不同的密钥长度推荐的加密轮数是不一样的,具体见下面的表格。
加密时明文按照 128 位为单位进行分组,每组包含 16 个字节,按照从上到下、从左到右的顺序排列成一个 4 × 4 的矩阵,称为明文矩阵。AES 的加密过程在一个大小同样为 4 × 4 的矩阵中进行,称为状态矩阵,状态矩阵的初始值为明文矩阵的值。每一轮加密结束后,状态矩阵的值变化一次。轮函数执行结束后,状态矩阵的值即为密文的值,从状态矩阵得到密文矩阵,依次提取密文矩阵的值得到 128 位的密文。
以 128 位密钥为例,密钥长度为 16 个字节,也用 4 × 4 的矩阵表示,顺序也是从上到下、从左到右。AES 通过密钥编排函数把密钥矩阵扩展成一个包含 44 个字的密钥序列,其中的前 4 个字为原始密钥用于初始加密,后面的 40 个字用于 10 轮加密,每轮使用其中的 4 个字。密钥递归产生规则如下:
-
如果 i 不是 4 的倍数,那么由等式 w[i] = w[i-4] ⊕ w[i-1] 确定;
-
如果 i 是 4 的倍数,那么由等式 w[i] = w[i-4] ⊕ T(w[i-1]) 确定;
加密的第 1 轮到第 9 轮的轮函数一样,包括 4 个操作:字节代换、行位移、列混合和轮密钥加。最后一轮迭代不执行列混合。另外,在第一轮迭代之前,先将明文和原始密钥进行一次异或加密操作。
解密过程仍为 10 轮,每一轮的操作是加密操作的逆操作。由于 AES 的 4 个轮操作都是可逆的,因此,解密操作的一轮就是顺序执行逆行移位、逆字节代换、轮密钥加和逆列混合。同加密操作类似,最后一轮不执行逆列混合,在第 1 轮解密之前,要执行 1 次密钥加操作。
AES 加密的轮函数操作包括以下方面:
-
字节代换 SubBytes:矩阵中的各字节通过一个 8 位的 S-box 进行转换。这个步骤提供了加密法非线性的变换能力。S-box 与 GF(2^8)上的乘法反元素有关,已知具有良好的非线性特性。为了避免简单代数性质的攻击,S-box 结合了乘法反元素及一个可逆的仿射变换矩阵建构而成。此外在建构 S-box 时,刻意避开了固定点与反固定点,即以 S-box 替换字节的结果会相当于错排的结果。
-
行位移 ShiftRows:在此步骤中,每一行都向左循环位移某个偏移量。在 AES 中(区块大小 128位 ),第一行维持不变,第二行里的每个字节都向左循环移动一格。同理,第三行及第四行向左循环位移的偏移量就分别是 2 和 3。128 位和 192 位的区块在此步骤的循环位移的模式相同。经过 ShiftRows 之后,矩阵中每一竖列,都是由输入矩阵中的每个不同列中的元素组成。Rijndael 算法的版本中,偏移量和 AES 有少许不同;对于长度 256 比特的区块,第一行仍然维持不变,第二行、第三行、第四行的偏移量分别是 1 字节、2 字节、3 字节。除此之外,ShiftRows 操作步骤在 Rijndael 和 AES 中完全相同。
-
列混合 MixColumns:在 MixColumns 步骤,每一列的四个字节通过线性变换互相结合。每一列的四个元素分别当作 1 , x , x^2 , x^3 的系数,合并即为GF(2^8)中的一个多项式,接着将此多项式和一个固定的多项式 c(x)=3x^3+x^2+x+2 在 modulo x^4 + 1 下相乘。此步骤亦可视为 Rijndael 有限域之下的矩阵乘法。MixColumns 函数接受 4 个字节的输入,输出 4 个字节,每一个输入的字节都会对输出的四个字节造成影响。因此 ShiftRows 和 MixColumns 两步骤为这个密码系统提供了扩散性。
-
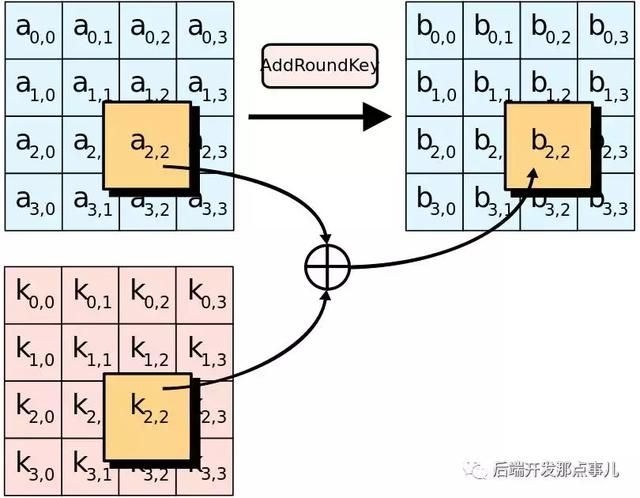
轮密钥加 AddRoundKey:回合密钥将会与原矩阵合并。在每次的加密循环中,都会由主密钥产生一把回合密钥(通过 Rijndael 密钥生成方案产生),这把密钥大小会跟原矩阵一样,以与原矩阵中每个对应的字节作异或(⊕)加法。
2、非对称加密算法RSA
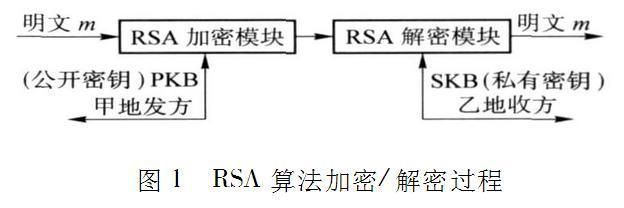
1977 年三位数学家 Rivest、Shamir 和 Adleman 设计了一种算法,可以实现非对称加密,也就是本文要讨论的 RSA 算法,使用非对称加密算法需要生成公钥和私钥,使用公钥加密,使用私钥解密。
互质关系:首先回顾一下质数的定义。质数 (prime number) 又称素数,有无限个。一个大于 1 的自然数,除了 1 和它本身外,不能被其他自然数整除,换句话说就是该数除了 1 和它本身以外不再有其他的因数;否则称为合数,如果两个正整数,除了 1 以外,没有其他公因子,我们就称这两个数是互质关系。互质关系不要求两个数都是质数,合数也可以和一个质数构成互质关系。
欧拉函数:对正整数 n,欧拉函数是小于 n 的正整数中与 n 互质的数的数目,用 φ(n) 表示。例如 φ(8) = 4,因为 1 3 5 7 均和 8 互质。欧拉函数可以表示为![]()
其中 p1, p2 …… pn 为 x 的所有质因数,x 是不为 0 的整数。且 φ(1) = 1。每种质因数只用一个。比如 12 = 2 * 2 * 3 那么
φ(12) = 12 * ( 1 - 1 / 2) * ( 1 - 1 / 3 ) = 4
若 n 是质数 p 的 k 次幂,除了 p 的倍数外,其他数都跟 n 互质,则数学公式为
![]()
若 m,n 互质,则数学公式为
![]()
当 n 为奇数时,则数学公式为
![]()
当 n 为质数时,则数学公式为
![]()
模反元素:如果两个正整数 a 和 n 互质,那么一定可以找到整数 b,使得 ab - 1 被 n 整除,或者说 ab 被 n 除的余数是 1。这时,b 就叫做 a 的 “模反元素”。表示如下:ab≡ 1 (mod n)
比如3 和 11 互质,那么 3 的模反元素就是 4,因为 (3 × 4) - 1 可以被 11 整除。显然,模反元素不止一个,4 加减 11 的整数倍都是 3 的模反元素 {…, -18, -7, 4, 15, 26, …},即如果 b 是 a 的模反元素,则 b + k n 都是 a 的模反元素。
欧拉定理:欧拉定理是一个关于同余的性质。欧拉定理表明,若 n,a 为正整数,且 n,a 互质,则有
a^φ(n) ≡ 1 (mod n)
假设正整数 a 与质数 p 互质,因为 φ(p) = p-1,则欧拉定理可以写成
a^(p-1) ≡ 1 (mod p)
RSA 公钥与私钥的生成:
生成密钥的过程如下:
-
首先选择两个质数 p 和 q,并且越大越好。
-
计算出 n = pq ,n 的二进制位数即为密钥的位数。
-
计算出 n 的欧拉函数
φ(n) = φ(p)φ(q) = (p-1) (q-1)
-
随机选择一个整数 e,条件是 1 < e < φ(n),且 e 与 φ(n) 互质
-
计算 e 对于 φ(n) 的模反元素 d
ed ≡ 1 (mod φ(n))
上面的公式等价于如下的一元二次方程,d 和 k 有无穷多种组合方式,选取一个 d 值即可
ed + k φ(n) = 1
-
将 n 和 e 封装成公钥,n 和 d 封装成私钥
RSA 加密与解密:
使用公钥 (n,e) 进行加密的过程,可以表示为如下公式,实际上就是根据明文 m
计算出密文 c 的过程。m 必须是整数(字符串可以取 ascii 值或 unicode 值),且 m 必须小于 n。
m^e ≡ c (mod n)
使用私钥 (n,d) 进行解密的过程,可以表示为如下公式,实际上就是根据密文 c 计算出明文 m 的过程。此处证明比较复杂,感兴趣的朋友可以自己看一下。
c^d ≡ m (mod n)
RSA 加解密过程示例:
首先生成密钥:
-
取 p = 61, q = 53
-
计算出 n = 61 * 53 = 3233
-
计算出 n 的欧拉函数 φ(3233) = 60 * 52 = 3120
-
随机选择一个整数 e = 17
-
计算 e 对于 φ(n) 的模反元素 d = 2753
使用公钥进行加密,假设明文 m = 65,表示大写字母 A,根据公式计算出密文为 2790。
65^17 ≡ 2790 (mod 3233)
使用私钥进行解密,密文为 2790,根据公式可以计算出明文为 65,表示大写字母 A。
2790^2753 ≡ 65 (mod 3233)
3、总结
数学是大数据算法的后台支持,如果你真的想从事IT、人工智能行业,那么学好数学是不可缺少的,从现在开始努力吧!