拉格朗日乘子法、KKT条件、线性规划对偶理论

转自：http://blog.csdn.net/Mr_KkTian/article/details/53750424

本文主要讲述给定一个线性规划，我们为什么能按照对偶规则，机械地并且非常容易地写出其对偶。当然为便于理解，本文先介绍了什么是拉格朗日乘子法、 KKT(KarushKuhnTucker) 条件。二者是求解有约束条件的优化问题的两个重要方法。

1.优化问题常见类型

通常我们需要求解的最优化问题有如下3类：
(i) 没有约束条件:

minf(x)

(ii) 有等式约束的优化问题，可以写为:

minf(x)

s.t.gi(x)=0;i=1,...,m

(iii) 再加入不等式约束的优化问题，可以写为

minf(x)

s.t.gi(x)<=0;i=1,...,m

hi(x)=0;i=1,...,p

对于第(i)类的优化问题，我们先求取f(x)的导数，然后令导函数为零，可以求得候选极大值或极小值，再在这些值中选取最优解；如果是凸函数，可以保证是最优解。

2.拉格朗日乘子法

对于上面第(ii)类的优化问题，常常使用的方法就是拉格朗日乘子法（Lagrange Multiplier) ，即把等式约束 gi(x) 用一个系数与 f(x) 写为一个式子，称为拉格朗日函数，而系数称为拉格朗日乘子。通过拉格朗日函数对各个变量求导，令其为零，可以求得候选值集合，然后验证求得最优值。为什么可以这样呢？接下来我们给予证明:
我们考虑下面问题：

minf(x,y)

s.t.g(x,y)=0

我们首先画出函数 f(x,y) 的等高线，然后画出 g(x,y)=0 这条曲线如下图：

我们的目标就是要字 g(x,y)=0 这条曲线上找一个点使 f(x,y) 的值尽可能小。我们现在观看等高线 f(x,y)=2 ，发现它与 g(x,y)=0 有两个交点，我们想象当 f(x,y) 的值不断变小时， g(x,y)=0 与等高线从有两个交点到若即若离的状态（一个交点，相切），最后没有交点。只有到等高线与曲线 g(x,y)=0 相切的时候，可能取得最优值，如上图所示，即等高线和曲线 g(x,y)=0 在该点的法向量必须有相同方向。因此最后最优解肯定是若即若离的点处取得。这个若即若离的数学表示方法就是： g(x,y)=0 和与等高线相切，这个点就是我们的目标点。
我们知道这个目标点的切线与函数 f(x,y) 和曲线 g(x,y)=0 在该点的法线都垂直，因此二者的法线是共线的(由高中的数学知识可以知道)。然后我们知道法线可以用该点的梯度表示，因此 我们可以得到目标点 (x∗,y∗) 处：

▽f(x∗,y∗)=λ▽g(x∗,y∗)

▽L(x∗,y∗,λ)=0

于是我们构造函数：

L(x,y,λ)=f(x,y)−λg(x,y)

求解它的最优解就等价于求原带约束的优化问题的最优解。

3. KKT条件(Karush Kuhn Tucker)

KKT条件其实可以看成是拉格朗日乘子法的进一步推广。对于上面第(iii)类的优化问题，如何求取最优值呢？常用的方法是KKT条件。我们看下面带不等式约束的优化问题:

minf(x)

s.t.gi(x)≤0,i=1,2,...m

我们的目标是在下图中阴影去或者边界找到一个点使得目标函数值最小。

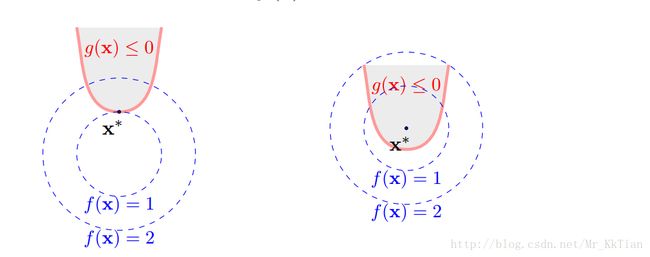
要求 g(x, y) ≤ 0，也就是是说图中的阴影区我们是要在阴影区或者边界上找一个点，使得 f(x, y) 最小，我们把他分成两种情况：
1. 如果最优解恰好在这条边界上，那么这个就可以通过拉格朗日来求解。
2. 如果最优解在阴影区内部，我们是要找最优解，这个最优解不在边界上，在他内部，如果在内部那这个解一定是单纯考虑 f(x, y) 的最优解，也就是直接求 ▽f(x,y)=0 的解。
我们写出拉格朗日函数如下：

L(x,λ)=f(x)−∑i=1mλigi(x)

我们将上述最优解情况1和2统一表出成，在最优解 x=x∗ 处，应满足以下条件(KKT条件):
1.(StationaryPoint)▽L(x∗,λ)=0
2.(PrimalFeasibility)g(x∗)≤0
3.(DualFeasibility)λi≤0,i=1,2,...,m
4.(ComplementarySlackness)λigi(x∗)=0,i=1,2,...,m

4.从广义拉格朗日(KKT)到线性规划对偶（优化对偶理论）

对于给定的一个LP模型：

min:cTx

s.t.Ax≥b

x≥0

我们写出其拉格朗日函数：

L(x,λ)=cTx−∑i=1mλi(ai1x1+ai2x2+...ainxn−bi)

当 λ>0 时，并且x是可行解的时候， cTx≥L(x,λ) ，即拉格朗日是原问题的一个下界。再进一步讨论我们有下面不等式成立：

cTx≥L(x,λ)≥infxL(x,λ)式(1)

infxL(x,λ)=infx(cTx−∑mi=1λi(ai1x1+ai2x2+...ainxn−bi))

=infx[λTb+(cT−λTA)x]

={λTb,−∞,if cT≥λTA and x≥0otherwise

现在我们定义拉格朗日对偶函数如下:

g(λ)=infxL(x,λ)

式(1)则可写成：

cTx≥L(x,λ)≥g(λ)

g(λ)=λTb 是当 cT≥λTA and x≥0 情况下，函数 f(x) 的下边界。也就是说：如果我们要求 λ≥0 ，并且 x 是可行解的话，那么我们原先的目标函数肯定比 L(x,λ) 要大。而 L(x,λ) 一定大于等于 g(λ) 。这里的 g(λ) 就是拉格朗日对偶。

现在我们给出任意一个 f(x) ，我们现在可以通过拉格朗日搭一下桥，我们想 minf(x) ，现在可以得到 f(x)≥L(x,λ)≥g(λ) ，所以得到我要 min f(x)，最小最小不可能比 g(λ) 要小了，所以我们就 maxg(λ) ，任何一个 g(λ) 都要比 f(x) 要小，所以最大的值 g(λ∗) 就是 f(x) 的最小值, 所以将 λ 换成 y 就是我们所要得到的对偶。

现在我们去求解原问题目标函数 f(x) 的最好的下边界，即：

max:λTb

s.t.λTA≤cT

λ≥0

线性规划中的对偶问题写法就是用 y 取代 λ

4.线性规划原问题与对偶问题

画出原函数、拉格朗日函数、对偶函数图如下：我们可以知道 原先要 min 的目标函数大于等于拉格朗日，拉格朗日大于等于 对偶目标函数，也就是说 mincTx≥L(x,y)≥yTb ，所以通过拉格朗日搭了一下桥，所以我们原先的目标函数一定大于对 偶的目标函数。

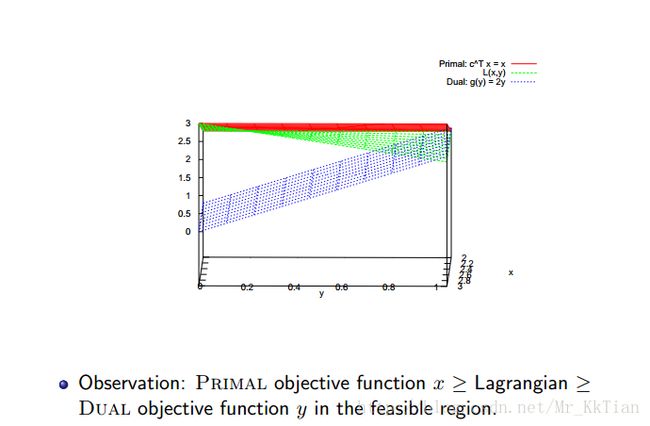
对偶性质总结：
(1).对偶的对偶就是原问题
(2).对于一般问题，对偶问题的任意一个可行解总是原问题的一个下界,也叫弱对偶性
(3).对于线性规划，原问题的存在最优解，那对偶问题也存在一个最优解，它们的数值相等，也叫强对偶性
(4).互补松弛性:假如 x 是原问题的可行解， y 为对偶问题的可行解，那么 x 和 y 是最优解时，当且仅当：
• 1≤i≤m，ui=yi(ai1x1+ai2x2+...+ainxn−bi)=0
• 1≤j≤n，vj=(cj−a1jy1−a2jy2−...−amjym)xj=0