动态规划-07distinct-subsequences给定一个字符串 S 和一个字符串 T,计算在 S 的子序列中 T 出现的个数java实现
题目描述
给定一个字符串 S 和一个字符串 T,计算在 S 的子序列中 T 出现的个数。
一个字符串的一个子序列是指,通过删除一些(也可以不删除)字符且不干扰剩余字符相对位置所组成的新字符串。(例如,"ACE" 是 "ABCDE" 的一个子序列,而 "AEC" 不是)
示例 1:
输入: S ="rabbbit", T ="rabbit" 输出: 3解释: 如下图所示, 有 3 种可以从 S 中得到"rabbit" 的方案。 (上箭头符号 ^ 表示选取的字母)rabbbit^^^^ ^^rabbbit^^ ^^^^rabbbit^^^ ^^^
示例 2:
输入: S ="babgbag", T ="bag" 输出: 5解释: 如下图所示, 有 5 种可以从 S 中得到"bag" 的方案。 (上箭头符号 ^ 表示选取的字母)babgbag^^ ^babgbag^^ ^babgbag^ ^^babgbag^ ^^babgbag^^^
思路:一开始遇到子集,子序列问题,想到的是用回溯方法(详见回溯法求子集)求出S中所有长度和T相等的子集,然后与T比较得到相同的数量。
import java.util.ArrayList;
public class Solution {
int num=0;
int flag=1;
public int numDistinct(String S, String T) {
if(S==null||T==null)
return 0;
int len1=S.length();
int len2=T.length();
if(len2>len1){
return 0;
}
ArrayList list=new ArrayList();
backtracking(S,T,len2,0,list);
return num;
}
public void backtracking(String S,String T,int k,int start,ArrayList list){
if(k<0){
return;
}
else if(k==0){
for(int i=0;i
方法能在LeetCode上通过,但45 / 63 个通过测试用例,显示时间超时,当字符串长度增大时求解的耗时也增大,因此无法在规定时间内完成。
故下文采用动态规划思想:(遇到这类问题最好方法就是列出表格,结合数据分析动态规划递推方程)
我们设置一个二维数组dp(i)(j)来记录长度为i的字串在长度为j的母串中出现的次数,这里长度都是从头算起的,而且遍历时,保持子串长度相同,先递增母串长度,母串最长时再增加一点子串长度重头开始计算母串。
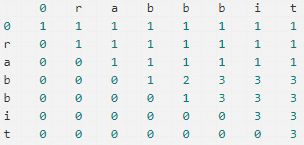
首先我们先要初始化矩阵,当子串长度为0时,所有次数都是1,当母串长度为0时,所有次数都是0。当母串子串都是0长度时,次数是1(因为都是空,相等)。接着,如果子串的最后一个字母和母串的最后一个字母不同,说明新加的母串字母没有产生新的可能性,可以沿用该子串在较短母串的出现次数,所以dp(i)(j) = dp(i-1)(j)。如果子串的最后一个字母和母串的最后一个字母相同,说明新加的母串字母带来了新的可能性,我们不仅算上dp(i-1)(j),也要算上新的可能性。那么如何计算新的可能性呢,其实就是在既没有最后这个母串字母也没有最后这个子串字母时,子串出现的次数,我们相当于为所有这些可能性都添加一个新的可能。所以,这时dp(i)(j) = dp(i-1)(j) + dp(i-1)(j-1)。下图是以rabbbit(i)和rabbit(j)为例的矩阵示意图。计算元素值时,当末尾字母一样,实际上是左方数字加左上方数字,当不一样时,就是左方的数字。
示意图
public class Solution {
public int numDistinct(String S, String T) {
if(S==null&&T==null)
return 1;
if(S==null&&T!=null)
return 0;
if(S!=null&&T==null)
return 1;
int[][]dp=new int[S.length()+1][T.length()+1];
dp[0][0]=1;
for(int i=1;i<=S.length();i++){
dp[i][0]=1;
}
for(int i=1;i<=T.length();i++){
dp[0][i]=0;
}
for(int i=1;i<=S.length();i++){
for(int j=1;j<=T.length();j++){
if(S.charAt(i-1)!=T.charAt(j-1)){
dp[i][j]=dp[i-1][j];
}
else{
dp[i][j]=dp[i-1][j]+dp[i-1][j-1];
}
}
}
return dp[S.length()][T.length()];
}
}