Deep Learning中的一些Tips详解（RELU+Maxout+Adam+Dropout）

本文主要讲如果我们的Deep Learning出现了一些不好的结果，我们该怎么办。学习前请先参考：反向传播算法(Backpropagation)----Gradient Descent的推导过程

一、概述

总得来说，所有的改进方法都可以用下面这张图来总体概括：

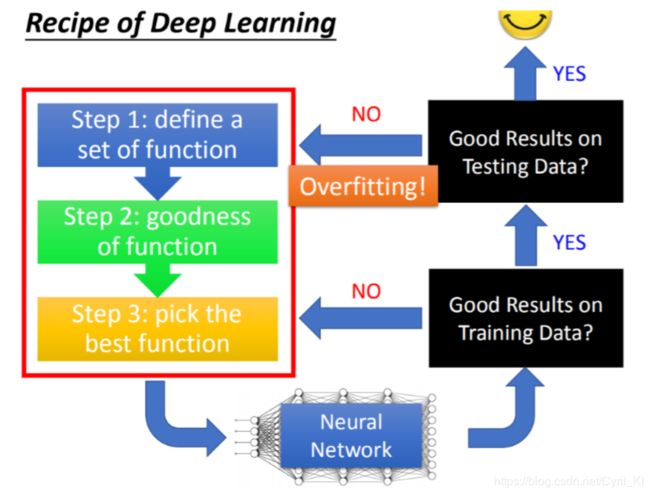
经历深度学习的三个步骤之后，我们得到了一个NN。那么首先我们应该检查该NN在训练集上面的表现，如果连训练集都不能很好的拟合，那么就应该检查那三个步骤我们是否可以有修改的地方。 如果训练集表现很好，那么就用测试集来检查这个NN，测试集上表现很好，那么这个模型就可以投入使用了，否则就是overfitting！！ 因此overfitting一定是先在训练集上面表现好了，才有可能出现。
这个也算是深度学习与机器学习的区别了，一些机器学习的方法比如SVM等，很容易在training set上得到一个比较好的表现，深度学习并不是这样，因此我们首先需要在训练集上进行验证！！
因此，针对目的来找解决方案，所有的改进无非就是分为两类：

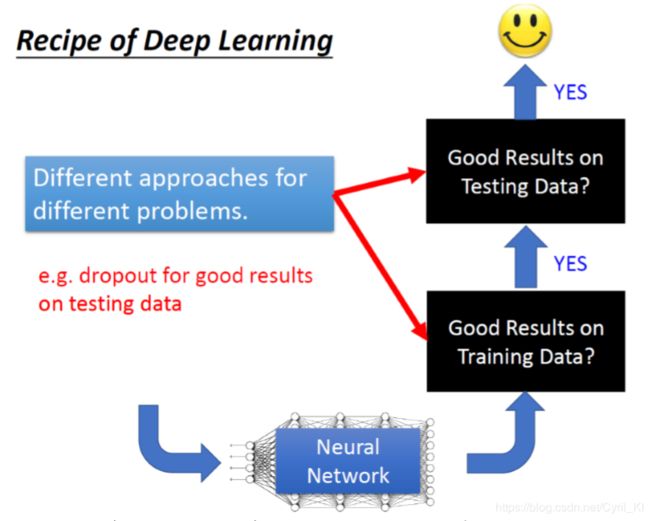
要么就是为了让模型在训练集上表现更好，要么就是让模型在测试集上表现更好。比如dropout是在training data上表现好，testing data上表现不好的时候才会去使用，当training data 结果就不好的时候用dropout 往往会越训练越差。 关于Dropout后面会讲到。

二、training set上表现不好

1.新的激活函数

关于激活函数，在逻辑回归以及BP算法的讲解中，我们都只是接触了Sigmoid Function。当我们使用Sigmoid function时，往往会出现以下问题：

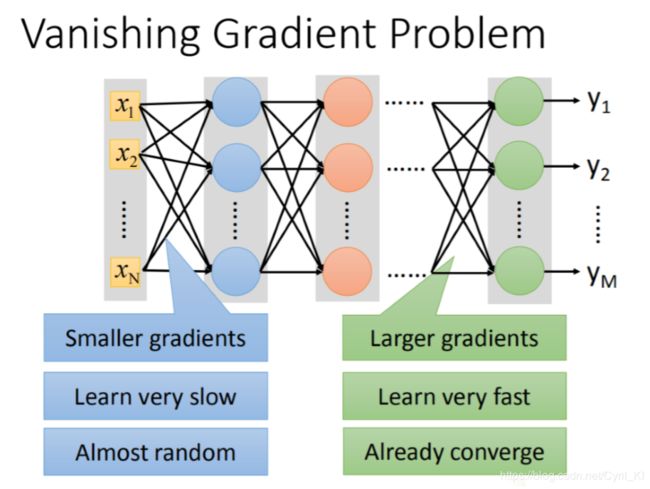
当网络比较深的时候，容易出现Vanishing Gradient Problem。所谓梯度消失，是指比较靠近input layer的几层Gradient值较小，而靠近output layer的较大，那么当使用梯度下降法寻求最优解时，当我们设定相同的learning rate，靠近输入层的参数更新会比较慢，而靠近输出层的参数更新比较快！！后面很快就收敛了，那么就停止学习了！！

为什么梯度值前面小后面大？

我们该怎么判断一个梯度值是大还是小呢？在Forward pass中我们很容易就可以得到$\frac{\partial z}{\partial w}$，然后在Backward pass中我们又可以得到$\frac{\partial l}{\partial z}$，二者相乘，就是一个梯度值$\frac{\partial l}{\partial w}$，评判这个值是否很大，我们可以用斜率的思想去考虑：假设求导很大，那么就相当于斜率很大，那么当w变化即使很小时，l变化也会非常的大！！ 这句话应该还是比较好理解哈。所以我们可以假定w变化了一个非常小的幅度$\Delta w$时，如果输出变化非常大，那么我们就可以说这个梯度值很大。
我们再来看看Sigmoid的函数：

从函数图像我们可以看出来，定义域是R，而值域是(0,1)，假设x变化非常大，比如我从1000变化到1000000，但是y变化是非常小的。

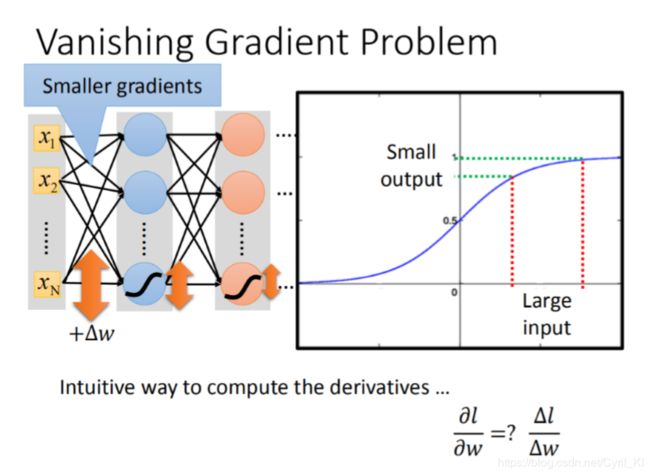
假设第一层的w变化了一个$\Delta w$，由于激活函数是Sigmoid，那么第一层的输出也就变化很小了，第一层的输出又是第二层的输入，输入变化导致第二次的输出也发生了变化，但是变化更小了…以此类推，最后的输出变化也就非常小了，所以越靠近后面层，梯度值是越大的。

至于解决办法，一种比较容易想到的思维就是，既然你越靠后梯度值越大，那么越靠后我可以设置learning rate越小，这样就可以减缓它的更新速度，不至于太快。 但是这种不太容易实现，我们更喜欢的方式是换掉Sigmoid。因为Sigmoid才是“祸害之源”。

2.RELU

线性整流函数（Rectified Linear Unit, ReLU），又称修正线性单元，是一种人工神经网络中常用的激活函数（activation function），它函数表达式为：
$f(x)=max(0,x)$，图像长成这样：

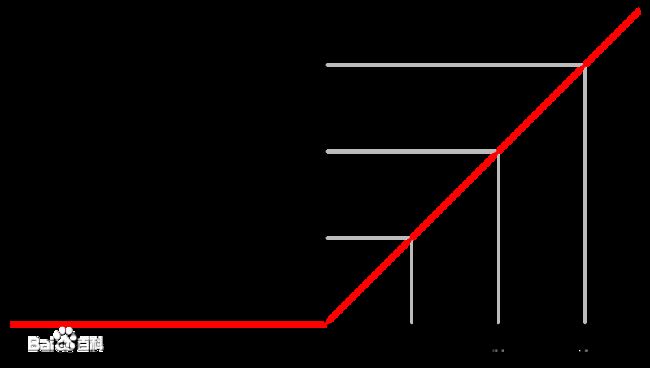
使用RELU作为激活函数，优势在哪里？最大的优势就是可以处理上面提到的梯度消失的问题。
将激活函数换成RELU之后：

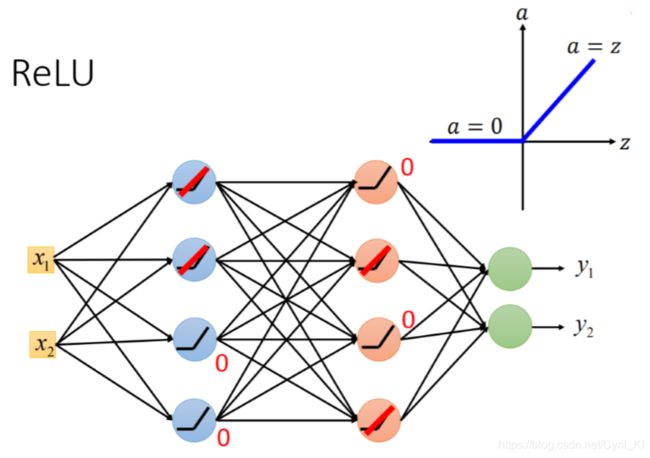
如果输入小于0，那么输出就是0，如果输入大于0，那么输出就是本身。
这里的好处就是，如果一个neural的输出是0，那么它对最终的输出y1,y2是没有影响的，因此可以将这些神经元直接拿掉，如下所示：

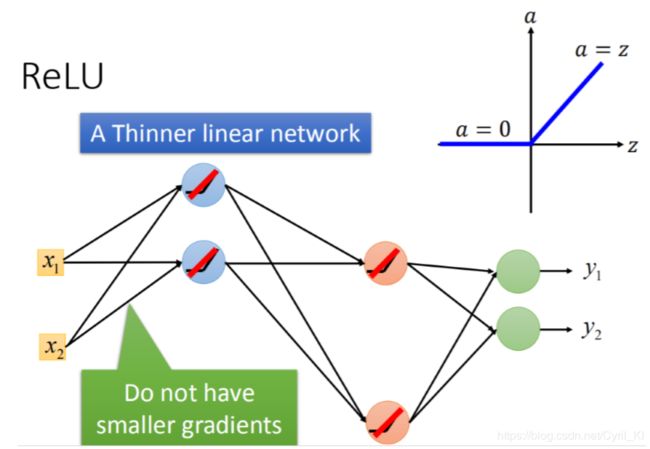
输入等于输出，不会像Sigmoid那样将一个很大的输入变成一个很小的输出，那么前后层的梯度值就不会像先前那样，所以就解决了梯度消失的问题。
但是这样一来，好像就有了一点问题，好像结构就变得是线性了，因为输入等于输出，就不能处理一些比较复杂的模型。但是实际上以RELU为激活函数的NN只是小范围内是线性的，总体来说还是非线性的。 这句话怎么理解呢？假设我输入的x1,x2使得当前的网络长成这个样子，但是一旦我换两个数据，这两个输入的数据相比较于x1,x2变化很大，那么NN也就变化了，所以它不是线性的。

3.RELU的变形

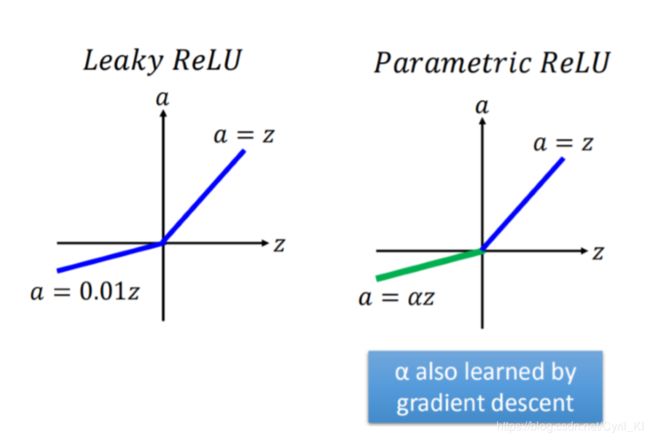
在z<0的时候，我们可以乘上一个系数$\alpha$，来使得模型更加的复杂一些，这个很好理解。

3.Maxout

1.思想

我们可以不用自已一开始就选好所有神经元的激活函数，而是通过training set来学习，然后决定每一个神经元应该用什么激活函数，这个就是Maxout的思想。

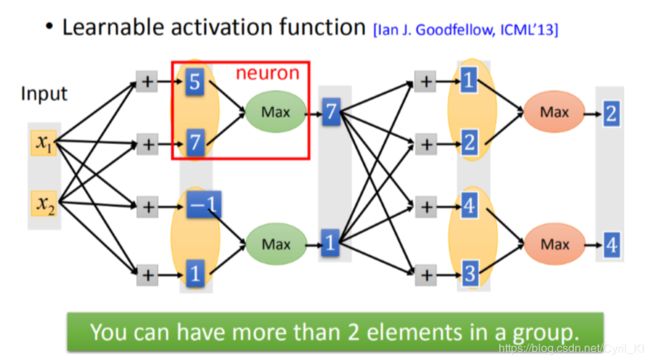
假设输入的是x1,x2，x1,x2乘以weight得到5,7,-1,1。这些值原本是通过ReLU或者sigmoid function得到的。而在Maxout里面，会将这些值进行分组，在组里选出一个最大的值当做真正的输出(选出7和1，这是一个vector 而不是一个value，7 和1再乘以不同的weight得到不同的value，然后再分组，再选出最大值，如上图所示。
那Maxout怎么训练出RELU？举个例子：

对于激活函数是RELU的神经元，如左图所示，我们输出得到z=wx+b，然后呢，将z再经过RELU处理，就变成了上述模样。而对于右边Maxout，z1=wx+b,z2=0，二者取max之后，也就变成了RELU，挺神奇的！！
一个线性和一个常数，取max之后，就是RELU。那假如不是一个常数呢？而是另一个线性函数，如图所示：

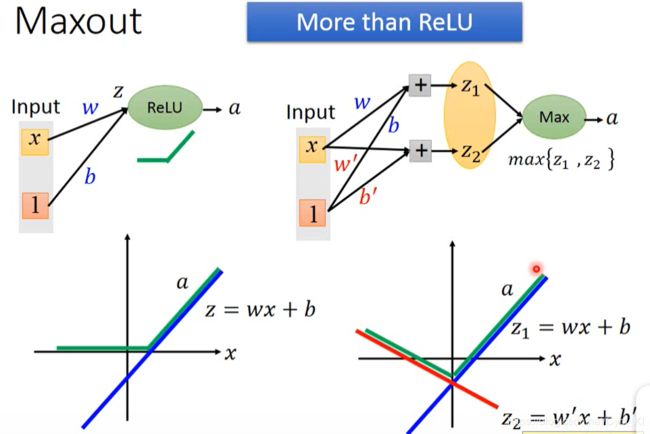
那最后的激活函数就变成了右边这个样子，因此我们只要适当地选择$w^{{}^{\prime }}$和$b^{{}^{\prime }}$这两个参数，就可以得到各种奇形怪状的激活函数。 而且上述两种情况还只是两个不同的函数组合，要是2个以上那就更加复杂了，也就能够满足我们的要求。

2.训练

那怎么用训练集来训练出每一个神经元的激活函数呢？答案也是Gradient Descent。那到底怎么train呢？因为可能有的人认为max这个函数不能够来求微分的，但实际上，我们可以这样考虑：

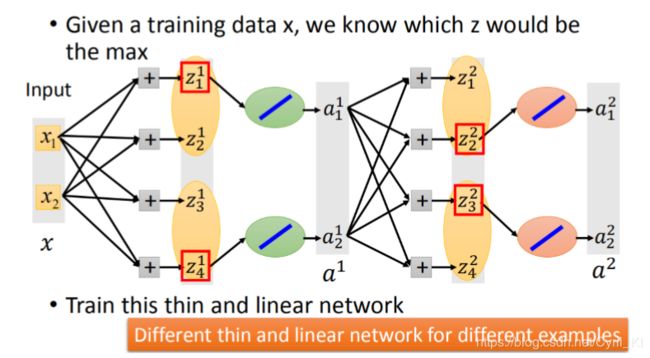
假设红框框部分是一个group里面比较大的一个，然后我们就可以把不是最大的神经元给去掉，如下所示：

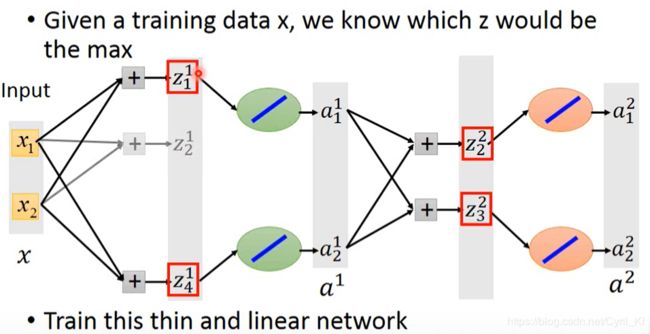
然后重点来了：我们可以把max函数换成y=x这个函数，从全局非线性变成了局部线性，这个时候就能够求微分了。当然有的人可能会考虑到去掉某些部分之后，有些w和b不就训练不到了么，须知，我们的数据有很多，以上这种结构仅仅只是输入为x1,x2的情况，加入换一个输入，那么NN的结构就不会是现在这个样子，因此我们可以训练到NN中所有的参数。 也即是说，不同的数据会唤醒不同的神经元，不会出现神经元死亡的情况。

4.梯度更新

如果讲到这里还不知道什么是梯度下降法，可以参考：BP推导

1.Adagrad

具体思想如下：

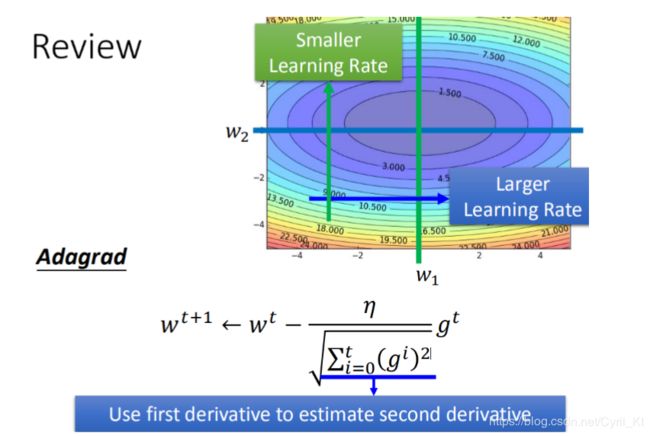
简单来说，learning rate不是一成不变的，而是用一个固定的learning rate来除以该参数过去所有梯度值的平方和再开根号，最后再乘上上一个梯度值，当前参数值减去上述这个乘积，就是新的参数。

2.RMSProp

RMSProp与Adagrad只有些许不同。不同的地方在于Adagrad除上的是以前所有梯度值的平方和然后再开平方，而RMSProp相对来说较为复杂一点，表达式如上图所示，计算还是相对简单的，只是这个参数$\alpha$该怎么理解呢？可以理解为当前的梯度值跟以往梯度值(指的是前几次加权后的梯度值，有点递归的意思了)的权重比较。也就是说，如果我把$\alpha$调整的特别小，那么我们就会认为当前的梯度值更为可信。

4.动量与惯性的思想

我们以前提到过，Gradient Descent可能会陷入局部最优，这个是很显然的道理：

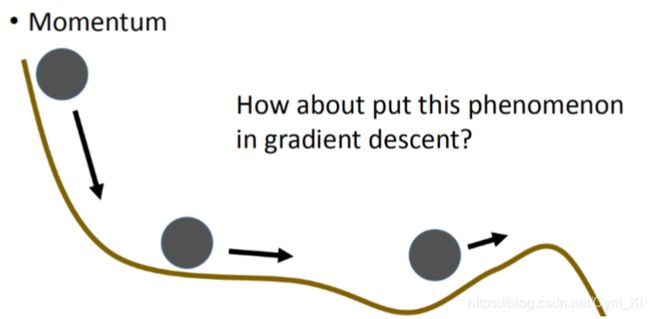
当我们的参数移动到某一个山谷的时候，梯度值已经为0了，但是这个位置很明显不是loss最低的位置，一般的方法当梯度值为0的时就已经停止参数更新的，于是得到了一个的local minimize。但在现实生活中，我们设想如下情景：
在一个山顶，给一个小球一个动量，它会往下滚，当它落到某一个山谷的时候，由于惯性它会继续往前走，但是如果已经落入了最低点，凭借惯性它也会继续往前走。但是如果它已经深陷最低点，那么它继续往上爬的可能性，或者说爬上去然后继续落入下一个不是最低点的可能性是很小的，因为能量不够。这样，我们就有可能解决局部最优的问题，为什么是有可能？因为如果局部最优的位置已经很低了，有可能凭借惯性，它也不足以爬上去，最后又只能落回来！！

Momentum的具体操作方法：
我们每次改变参数移动的方向时，不再只考虑gradient，而是现在的gradient加上前一个时间点移动的方向，前一个时间点的方向刚好就用来体现惯性。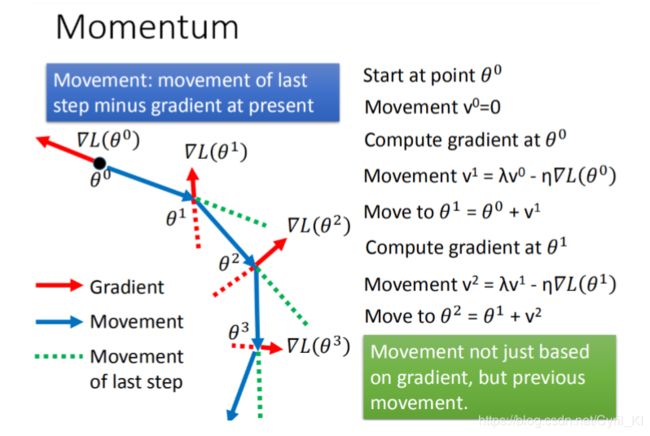
如上图所示，Gradient是我们算出来的当前的梯度值，我们应该向它的反方向运动，但是呢，我们现在不仅仅只是单方向的反方向运动，还要考虑前一次运动的方向，然后两个合成，构成新的前进方向。 注意，由于参数不止一个，所以梯度值算出来是一个向量，这一点千万要意识到。

5.Adam

Adam=RMSProp+Momentum。 二者结合的意思就是说，我们通过RMSProp来确定反方向的移动向量长度，然后还要考虑Momentum，也就是前一次的移动方向，最后二者合成得到最终的移动方向。

三、testing set上表现不好

1.Early Stopping

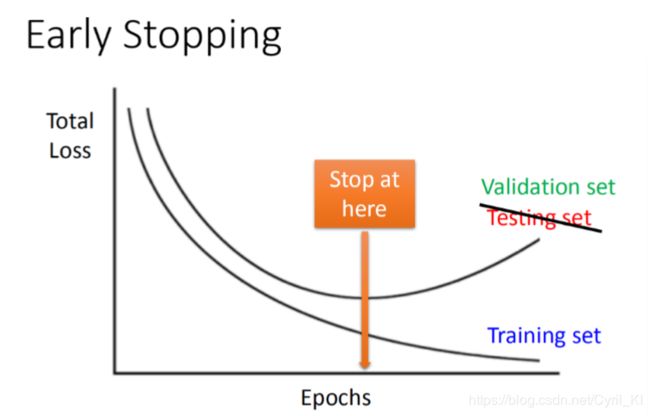
随着我们的训练，Total Loss会越来越小，无论是在训练集上还是测试集上，但是测试集上可能到达某一个点之后就会停下来，接着就开始增加了。 假设我们开了天眼，知道testing set在某一点会使得Total Loss最小，那么我们就应该停在这个地方，但是我们并不能开天眼。。。因此我们采用验证集的方式。我们会用validation set模拟testing set，什么时候validation set最小，你的training就会停下来。

2.Regularization

前面我们讲线性回归的时候有讲到这个正则化，就是在损失函数后面加上正则项，由此可以形成岭回归等等。 加正则项的目的是使得模型更加平滑，防止过拟合。（可以参考：机器学习之岭回归）
加上上述的正则化项之后，我们再用梯度下降的方法：（比较简单就不自己推了）

我们发现，原来是长成这个样子的：

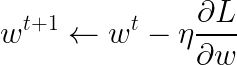
加上正则化项之后，变成：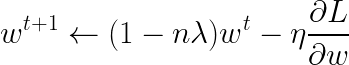
多出的$1-n\lambda$，这一项<1，每次乘上之后相当于会让$w^t$变小一些，最后会慢慢变小趋近于0，但是会与后一项梯度的值达到平衡，使得最后的值不等于0。

3.Dropout

这里我们不妨回忆一下前面讲集成学习时随机森林的策略：随机选取样本和特征来防止过拟合。Dropout有着类似的思想，我们每次都随机选取一些神经元丢弃掉，与之相连的部分也去掉，剩下的部分我们来训练参数。

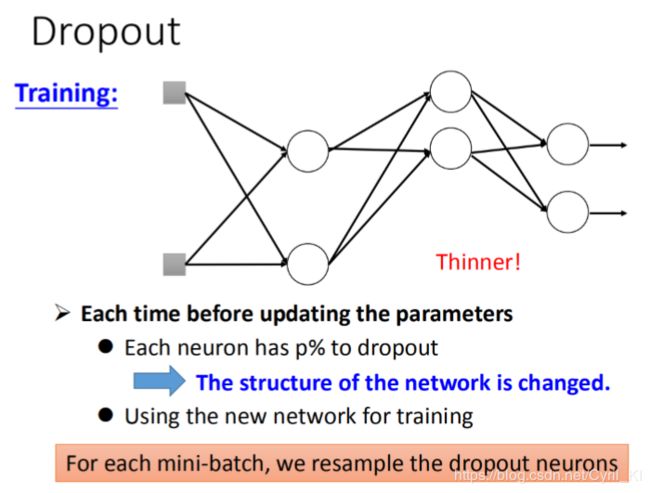
如上所示，我们选择“抓爆”（谐音）一些神经元之后，结构变得更加清晰明了了。注意，每次我们都需要重新选取新的神经元来进行Dropout，意思就是有些神经元可能会被“抓爆”多次，但是回想我们前面随机森林的讲解，某些特征虽然在某一次训练中没被选上，但是后面它总会有机会选上的，这里也是类似，我们不用担心某些参数没有被训练到。
Dropout有几点需要注意：

1. 在Testing的时候我们不用Dropout，只是在用训练集训练NN的时候才用Dropout。
2. 假设我们在训练的时候每一个神经元被“抓爆”的概率是p，那么当我们在测试集进行测试的时候，所有的weight都要乘上1-p。
3. 针对第二条，为什么要乘上一个系数1-p？因为我们训练的时候，随机“抓爆”了一些神经元，这样训练出来的模型，如果我们在Testing的时候不乘上一个系数的话，会使得Testing的结果跟真实结果相差很多。
4. “抓爆”会降低模型复杂度，减轻过拟合现象，这与我们一开始的初衷是一致的，也就是Training set上表现好，而Testing set上表现不好。

相信看过集成学习的人，会觉得Dropout比较好理解一些，因此Dropout也可以认为是Ensemble的一个终极版本！！！
这里需要注意的是，可能某些人会认为我们每次训练时training set都是一样的，只是我们会随机Dropout一些神经元，但是其实并不是这样子的，如下所示：

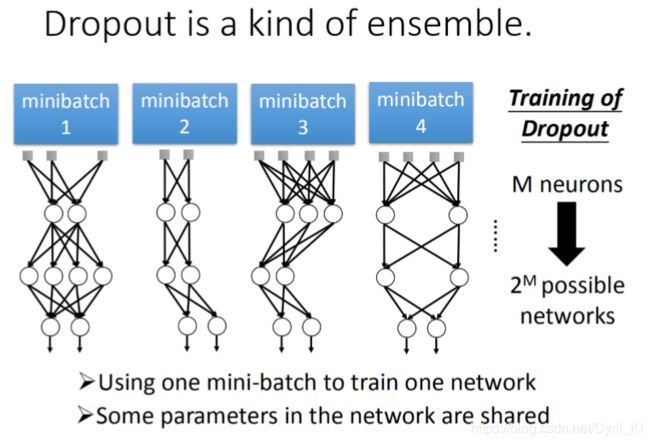
我们每次产生的数据集都是不一样的，每一个mini-batch里面的数据也是随机的，mini-batch数据随机+Dropout就是我们前面集成学习里面随机森林中的数据随机+特征随机。
既然是跟Ensemble差不多，那么后面就不再赘述。参考：
机器学习之Ensemble