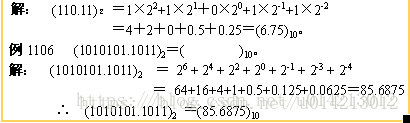c语言浮点数内存存储解析和浮点数（double、float）如何定义NaN、正无穷(inf)、负无穷(-inf)，以及如何判断是否是NaN

C语言浮点数存储方式

一. 浮点数内存存储方式

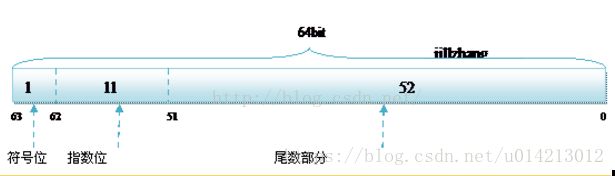
对于浮点类型的数据采用单精度类型(float)和双精度类型(double)来存储，float数据占用 32bit,double数据占用 64bit.其实不论是float类型还是double类型，在计算机内存中的存储方式都是遵从IEEE的规范的，float 遵从的是IEEE R32.24 ,而double 遵从的是R64.53。   

无论是单精度还是双精度，在内存存储中都分为3个部分：  

1) 符号位(Sign)：0代表正，1代表为负；  

2) 指数位(Exponent)：用于存储科学计数法中的指数数据，并且采用移位存储； 

3) 尾数部分(Mantissa)：尾数部分

其中float的存储方式如下图所示：

而双精度的存储方式为:

R32.24和R64.53的存储方式都是用科学计数法来存储数据的

用二进制的科学计数法第一位都是1嘛，干嘛还要表示呀？可以将小数点前面的1省略，所以23bit的尾数部分，可以表示的精度却变成了 24bit，道理就是在这里。

那24bit能精确到小数点后几位呢，我们知道9的二进制表示为1001，所以4bit能精确十进制中的1位小数 点，24bit就能使float能精确到小数点后6位，而对于指数部分，因为指数可正可负，8位的指数位能表示的指数范围就应该为:-127-128了， 所以指数部分的存储采用移位存储，存储的数据为元数据+127。

 

  二. 十进制小数转换为二进制小数

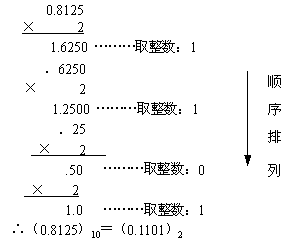
 十进制小数转换成二进制小数采用"乘2取整，顺序排列"法。具体做法是：用2乘十进制小数，可以得到积，将积的整数部分取出，再用2乘余下的小数部分，又得到一个积，再将积的整数部分取出，如此进行，直到积中的小数部分为零，或者达到所要求的精度为止。 然后把取出的整数部分按顺序排列起来，先取的整数作为二进制小数的高位有效位，后取的整数作为低位有效位。

    【例1】把（0.8125）转换为二进制小数。
    解： 

   【例2】（173.8125）10＝（ ）2

解：（173）10＝（10101101）2
由［例1］得（0.8125）10＝（0.1101）2
把整数部分和小数部分合并得： （173.8125）10＝（10101101.1101）2

下面就看看8.25和120.5在内存中真正的存储方式：

首先看下8.25，用二进制的科学计数法表示为 ，首先(8.25)10 = (1000.01)2=(1.00001*2^3)
=1.00001*2^3  按照上面的存储方式，符号位为0，表示为正；指数位为3+127=130，位数部分为 1.00001，故8.25的存储方式如下：  0x41040000 = 0100  0001 0000 0100 0000 0000 0000 0000 

分解如下：0--10000010--00001000000000000000000  

符号位为0，指数部分为10000010，位数部分为 00001000000000000000000

 

同理，120.5在内存中的存储格式如下： (120.5)10 = (01111000.1)2=(1.1110001*2^6)

=1.1110001*2^6  按照上面的存储方式，符号位为0，表示为正；指数位为6+127=133，位数部分为 1.1110001，故120.5的存储方式如下：  0x41040000 = 0100  0010 1111 0001 0000 0000 0000 0000 

 0x42f10000:    0100  0010 1111 0001 0000 0000 0000 0000  

分解如下：0--10000101--11100010000000000000000  

 

  三. 二进制小数转换为十进制小数

    由二进制小数转换成十进制小数的基本做法是，把二进制数首先写成加权系数展开式，然后按十进制加法规则求和。这种做法称为"按权相加"法。
    例1 把二进制小数110.11转换成十进制小数。

那么如果给出内存中一段数据，并且告诉你是单精度存储的话，你如何知道该数据的十进制数值呢？其实就是对上面的反推过程，比如给出如下内存数据： 01000001001000100000000000000000 

第一步：符号位为0，表示是正数；  

第二步：指数位为10000010，换算成十进制为130，所以指数为130-127=3；

第三步：尾数位为01000100000000000000000，

第四步:二进制表示为:1.01000100000000000000000因为指数为+3(右移3),-3(左移位3)所以也等价于

1010.00100000000000000000 = 10.00100000000000000000=10+(0/2+0/4+1/8)=10.125

【同例1】:换算成十进制为 (1+1/4+1/64)； 所以相应的十进制数值为：2^3*(1+1/4+1/64)=8+2+1/8=10.125

 

浮点数（double、float）如何定义NaN、正无穷、负无穷，以及如何判断是否是NaN

一.  原理

NaN ：指数位的每个二进制位全为1  并且尾数不为0；

无穷 ：指数位的每个二进制位全为1并且尾数为0；符号位为0，是正无穷，符号位为1是负无穷。

所以NaN、正无穷、负无穷可以如此定义，可以如此判断是否NaN：

二.  判断方法

static inline bool isInf(double d)
{
    uchar *ch = (uchar *)&d;
    if (QSysInfo::ByteOrder == QSysInfo::BigEndian) {
        return (ch[0] & 0x7f) == 0x7f && ch[1] == 0xf0;
    } else {
        return (ch[7] & 0x7f) == 0x7f && ch[6] == 0xf0;
    }

}

static inline bool isNan(double d)
{
    uchar *ch = (uchar *)&d;
    if (QSysInfo::ByteOrder == QSysInfo::BigEndian) {
        return (ch[0] & 0x7f) == 0x7f && ch[1] > 0xf0;
    } else {
        return (ch[7] & 0x7f) == 0x7f && ch[6] > 0xf0;
    }
}

static inline bool isFinite(double d)
{
    uchar *ch = (uchar *)&d;
    if (QSysInfo::ByteOrder == QSysInfo::BigEndian) {
        return (ch[0] & 0x7f) != 0x7f || (ch[1] & 0xf0) != 0xf0;
    } else {
        return (ch[7] & 0x7f) != 0x7f || (ch[6] & 0xf0) != 0xf0;
    }
}

static inline bool isInf(float d)
{
    uchar *ch = (uchar *)&d;
    if (QSysInfo::ByteOrder == QSysInfo::BigEndian) {
        return (ch[0] & 0x7f) == 0x7f && ch[1] == 0x80;
    } else {
        return (ch[3] & 0x7f) == 0x7f && ch[2] == 0x80;
    }
}

static inline bool isNan(float d)
{
    uchar *ch = (uchar *)&d;
    if (QSysInfo::ByteOrder == QSysInfo::BigEndian) {
        return (ch[0] & 0x7f) == 0x7f && ch[1] > 0x80;
    } else {
        return (ch[3] & 0x7f) == 0x7f && ch[2] > 0x80;
    }
}

static inline bool isFinite(float d)
{
    uchar *ch = (uchar *)&d;
    if (QSysInfo::ByteOrder == QSysInfo::BigEndian) {
        return (ch[0] & 0x7f) != 0x7f || (ch[1] & 0x80) != 0x80;
    } else {
        return (ch[3] & 0x7f) != 0x7f || (ch[2] & 0x80) != 0x80;
    }
}