[实例分割] SOLO: Segmenting Objects by Locations 论文阅读
转载请注明作者和出处: http://blog.csdn.net/john_bh/
论文链接: SOLO: Segmenting Objects by Locations
作者及团队:阿德莱德大学 & 字节跳动 AI Lab
会议及时间:Arxiv 2019.12
code1:开源github 地址1:https://github.com/WXinlong/SOLO
code2:开源github 地址2:https://github.com/Epiphqny/SOLO
作者解答:如何看待SOLO: Segmenting Objects by Locations,是实例分割方向吗?
文章目录
- 1.主要贡献
- 2. Method: SOLO
- 2.1 Problem Formulation
- 2.2 Network Architecture
- 2.3 SOLO Learning
- 2.4 Inference
- 3. Experiments
- 3.1 Ablation Experiments
- 3.2 SOLO-512
- 4. Decoupled SOLO
- 5. Error Analysis
- 6. SOLO for Instance Contour Detection
1.主要贡献
通过引入“实例类别”的概念,根据实例的位置和大小为实例中的每个像素分配类别,将实例分割转化为分类问题;- 与Mask R-CNN 相比,架构虽然更简单但是有效,是一种单阶段实例分割的方法。
SOLO的核心思想是根据位置和大小分离对象实例。
-
Locations:
将图像划分为 S × S S\times S S×S 个单元的网格,从而得出 S 2 S^2 S2 个中心位置类。根据对象中心的坐标,将对象实例分配给一个网格单元作为中心位置类别。 SOLO 与将掩码封装到通道轴中的DeepMask和TensorMask不同,SOLO 将中心位置类别编码为通道轴,类似于语义分割中的语义类别。每个输出通道负责一个中心位置类别,并且相应的通道图应预测属于该类别的对象的实例掩码。因此,结构的几何信息自然地保留在高宽比的空间矩阵中。本质上,实例类别近似于实例的对象中心的位置。因此,通过将每个像素分类到其实例类别中,等效于使用回归从每个像素预测对象中心。
将位置预测任务转换为分类,而不是回归,这样做的重要性在于,分类使用固定数量的通道对不同数量的实例进行建模更加简单明了,同时又不依赖后处理(比如分组或学习嵌入)。 -
Size:
为了区分不同尺度的实例,使用了特征金字塔(FPN:feature pyramid network),以便将物体的不同尺度映射到不同层次的特征图上,正如物体尺度上的类别。 因此,所有对象实例都分离,从而可以通过“实例类别”对对象进行分类。请注意,FPN旨在检测图像中不同大小的目标。作者证明了FPN是SOLO的核心组成部分之一,并且对分割性能有很明显的作用,特别是对不同大小的物体。
本质上,SOLO通过离散量化将坐标回归转换为分类。 这样做的一个好处是避免了在检测器(如YOLO)中使用的启发式坐标规范化操作和log转换。所提出的SOLO方法的简单性和强大的性能可以预测其在各种实例级识别任务中的应用。
![[实例分割] SOLO: Segmenting Objects by Locations 论文阅读_第1张图片](http://img.e-com-net.com/image/info8/755718c2a6fd4df39a6d7670f07e9b46.jpg)
2. Method: SOLO
2.1 Problem Formulation
给定任意图像,实例分割系统需要确定是否存在语义对象的实例。如果存在,则系统返回分割mask。SOLO框架的中心思想是将实例分割重新表示为两个同时发生的子问题:类别感知预测问题和实例感知掩码生成问题。具体而言,将输入图像统一划分为 S × S S\times S S×S 的网格 。如果对象的中心落入网格单元,则该网格单元负责预测语义类别(semantic category) 以及 分割该对象实例(segmenting that object instance)。
-
Semantic Category
对于每个网格,SOLO都会预测 C C C 维输出,用来表示语义类的概率。其中, C C C 是类别的数量。这些概率取决于网格单元,如果将输入图像划分为 S × S S×S S×S 网格,则输出空间将为 S × S × C S×S×C S×S×C。值得注意的是,这里假设 S×S 网格的每个单元必须属于一个单独的实例,也就是只属于一个语义类别。如图2所示:
![[实例分割] SOLO: Segmenting Objects by Locations 论文阅读_第2张图片](http://img.e-com-net.com/image/info8/45e3098cd1d94638b5c6aa4e28b5a53d.jpg)
-
Instance Mask
与语义类别预测并行,每个正样本网格单元还将生成相应的实例掩码。给定输入图像 I I I ,如果将其划分为 S × S S\times S S×S 网格,则总共最多会有 S 2 S^2 S2 个预测掩码。在3D输出张量中的第三维(通道)上直接对这些掩码进行编码。具体来说,实例掩码输出将具有 H I × W I × S 2 H_I \times W_I \times S^2 HI×WI×S2 维。第 k t h k^{th} kth 个通道将负责在网格 ( i , j ) (i,j) (i,j) 处分割实例,其中 k = i ⋅ S + j k=i\cdot S+j k=i⋅S+j ( i i i 和 j j j 从零开始)。 这样,在语义类别和class-agnostic 掩码之间建立了一对一的对应关系,如图2所示。引入 CoordConv: 预测实例掩码的直接方法是采用全卷积网络,例如语义分割中的FCN。然而,常规的卷积运算在某种程度上在空间上是不变的。空间不变性对于某些任务(例如图像分类)是理想的,因为它会引入鲁棒性。但是,相反,
这里需要一个空间变化的模型,或者更精确地说,是位置敏感的模型,因为分割掩码是以网格为条件,并且必须由不同的特征通道分开。根据“CoordConv”运算符的启发将标准化的像素坐标直接输入到网络中。具体来说,创建一个与输入相同的空间大小的张量,其中包含像素坐标,并将其标准化为 $[-1,1],然后将该张量连接到输入特征,并传递到后续图层。将输入的坐标信息给到卷积操作,这样就给传统的FCN 模型添加了空间功能。 应当指出,CoordConv不是唯一的选择。例如,半卷积算子(semi-convolutional)也可以,但使用CoordConv更简洁,很容易实现。如果原始特征张量的大小为 H × W × D H\times W\times D H×W×D ,则新张量的大小为 H × W × ( D + 2 ) H\times W\times (D+2) H×W×(D+2),其中最后两个通道为 [ x , y ] [x,y] [x,y] 像素坐标。
-
Forming Instance Segmentation
在SOLO中,类别预测和相应的掩码自然通过它们的参考网格单元关联起来,即 k = i ⋅ S + j k=i\cdot S+j k=i⋅S+j 。基于此,可以直接为每个网格形成最终实例分割结果,然后将所有网格结果汇总起来,就可以得到该图像的实例分割结果,最后,使用非极大抑制(NMS)获得最终实例分割结果,而不需要其他任何后处理操作。
2.2 Network Architecture
SOLO连接在卷积的主干网络之后。作者使用FPN,它会生成具有不同大小的特征图的金字塔,每个级别具有固定数量的通道(通常为256维)。这些特征图作为每个预测head的输入:语义类别和实例掩码。head的权重在不同级别上共享。网格数可能在不同的金字塔上有所不同。在这种情况下,仅不共享最后一个1×1卷积。
为了证明方法的通用性和有效性,作者使用多种架构实例化了SOLO。区别包括:
- 用于特征提取的骨干架构;
- 用于计算实例分割结果的head;
- 用于优化模型的训练损失函数。
大多数实验都基于图3中所示的head结构。作者还利用不同的变体来进一步研究通用性。注意到实例分割head具有简单的结构。
![[实例分割] SOLO: Segmenting Objects by Locations 论文阅读_第3张图片](http://img.e-com-net.com/image/info8/79454628d93a406cb6f4b2305efa39f9.jpg)
2.3 SOLO Learning
-
Label Assignment
类别预测分支,网络需要给出 S × S S\times S S×S 个网格的物体类别概率。具体来说,如果第 ( i , j ) (i,j) (i,j) 个网格和某个ground truth 掩码的center region重叠大于某阈值,则将其视为正样本;否则,它为负样本。给定 ground truth 掩码的中心点 ( c x , c y ) (c_x,c_y) (cx,cy) (这里的中心点并不是bbox的中心,而是质心),宽度 w w w 和高度 h h h ,center region由恒定比例因子 ϵ : ( c x , c y , ϵ w , ϵ h ) \epsilon:(c_x,c_y,\epsilon w,\epsilon h) ϵ:(cx,cy,ϵw,ϵh) 控制。将 ϵ \epsilon ϵ 设置为 0.2 0.2 0.2,每个ground truth 掩码平均有3个正样本。Mask预测分支,作者为每个正样本提供了一个二进制分割掩码。因为每个图像都有 S 2 S^2 S2 个网格,所以有 S 2 S^2 S2 输出掩码。对于每个正样本,对应的目标二进制掩模将被标注。可能有人担心,掩码的顺序会影响掩码预测分支,但是,作者表明,最简单的行优先顺序对这个方法很有效。
-
Loss Function
训练损失定义为公式1:
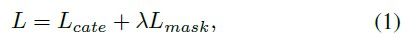
L c a t e L_{cate} Lcate 是传统的Focal loss ,针对语义类别分类问题, L m a s k L_{mask} Lmask 是掩码预测的损失函数:
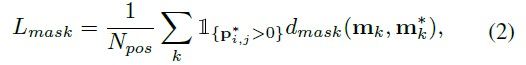
其中,索引 i = ⌊ k / S ⌋ , j = k m o d S i=\left \lfloor k/S \right \rfloor,\ j=k \ mod \ S i=⌊k/S⌋, j=k mod S ,其中索引顺序是从上到下,从左往右产生的。 N p o s N_{pos} Npos 是正样本的数量。 p ∗ , m ∗ p^*, m^* p∗,m∗ 分别代表了分类和掩码。 1 \mathbb{1} 1 是指标函数,如果 P i , j ∗ > 0 P^∗_{i,j}>0 Pi,j∗>0 则为1,否则为0。在实现中, 作者比较了 d m a s k d_{mask} dmask 的多个实现,主要是 二元交叉熵 (Binary Cross Entropy:BCE)、Focal Loss和Dice Loss。最终出于效率和稳定性,选用了Dice Loss, λ = 3 \lambda=3 λ=3 ,Dice Loss定义如公式3 :
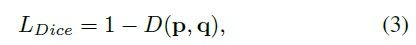
其中 D D D 为Dice系数,定义为:
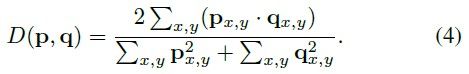
其中 p x , y , q x , y p_{x,y},q_{x,y} px,y,qx,y 分别为预测 soft mask p p p 和 ground truth mask q q q 在 ( x , y ) (x,y) (x,y) 位置的像素值。另外,作者在实验部分给出了更多损失函数的比较。
2.4 Inference
给定输入图像,将其通过骨干网络和FPN,并获得网格 ( i , j ) (i,j) (i,j) 处的类别得分 p i , j p_{i,j} pi,j 和相应的掩码 m k m_k mk ,其中 k = i ⋅ S + j k=i\cdot S+j k=i⋅S+j ,因为通常保持行优先。首先使用置信度阈值0.1来过滤低置信度的预测。然后,选择排名前500位的得分掩码,并将其输入到NMS操作中。要将预测的soft mask转换为二进制掩码,使用阈值0.5将二进制的预测的soft mask二进制化。我们保留前100个实例掩码进行评估。
3. Experiments
- Main Results: 在表1的MS COCO test-dev上,将SOLO与最新的实例分割方法进行了比较,结果如下如图:
![[实例分割] SOLO: Segmenting Objects by Locations 论文阅读_第4张图片](http://img.e-com-net.com/image/info8/692a773b34984cc9a110208745f1e61b.jpg)
SOLO 在COCO上测试可视化结果如图8所示:
![[实例分割] SOLO: Segmenting Objects by Locations 论文阅读_第5张图片](http://img.e-com-net.com/image/info8/f813b774590b4a75b16b374e9e00c21a.jpg)
- How SOLO Works?
图4 显示了 S = 12 S=12 S=12 网格生成的网络输出。子图 ( i , j ) (i,j) (i,j) 表示由相应的掩码通道(在Sigmoid之后)生成的soft mask预测结果。在这里可以看到不同的实例在不同的掩码预测通道上激活。通过在不同位置显式地分割实例,SOLO将实例分割问题转换为位置感知的分类任务。
![[实例分割] SOLO: Segmenting Objects by Locations 论文阅读_第6张图片](http://img.e-com-net.com/image/info8/949c4e958a954546b8823d877f040364.jpg)
在每个网格处将仅激活一个实例,并且可以由多个相邻的mask通道来预测一个实例。在推断过程中,使用NMS抑制这些冗余掩码。
3.1 Ablation Experiments
-
Grid number: 将网格数对性能的影响与单个输出特征图进行比较,如表2所示,结果表明,单尺度SOLO可适用于对象标度变化不大的某些场景。但是,单尺度模型在很大程度上落后于金字塔模型,这说明了FPN在处理多尺度预测中的重要性。
![[实例分割] SOLO: Segmenting Objects by Locations 论文阅读_第7张图片](http://img.e-com-net.com/image/info8/9b082bb048f2437dace33a79f9f90777.jpg)
-
Multi-level Prediction: 从表2中可以看出,单尺度SOLO在分割多尺度对象方面遇到了困难。在这种对比中表明,使用FPN的多级预测可以很大程度上解决此问题。从表2的对比开始,使用五个FPN金字塔分割不同比例的对象(表3)。明确使用ground-truth
mask的比例将其分配给金字塔的级别。基于多级预测,进一步实现了35.8%AP。正如预期的那样,所有指标的分割效果均得到了很大的改善。
![[实例分割] SOLO: Segmenting Objects by Locations 论文阅读_第8张图片](http://img.e-com-net.com/image/info8/0d17ffb60a2348539b4813fd4328ded2.jpg)
-
CoordConv: 如表4所示,标准卷积可以在某种程度上具有空间变异性。 通过级联额外的坐标通道使卷积访问其自己的输入坐标时,我们的方法享有3.6的绝对AP增益。 两个或多个CoordConv无法带来明显的改善。 这表明单个CoordConv已经使预测对空间变体/位置敏感。
![[实例分割] SOLO: Segmenting Objects by Locations 论文阅读_第9张图片](http://img.e-com-net.com/image/info8/5f827bc3d7e0427cb55d98632e2151ba.jpg)
-
Loss function: 表5比较了掩码优化分支的不同损失函数。这些方法包括常规的二叉熵(BCE)、Focal Loss(FL)和Dice Loss(DL)。Dice Loss无需手动调整损耗超参数即可获得最佳结果,Dice Loss可将像素视为一个整体,并可以自动在前景像素和背景像素之间建立适当的平衡。
![[实例分割] SOLO: Segmenting Objects by Locations 论文阅读_第10张图片](http://img.e-com-net.com/image/info8/f668b9e5b5a0472c925e39c780b2e250.jpg)
-
Alignment in the category branch: 在类别预测分支中,必须将空间大小为 H × W H\times W H×W 的卷积特征匹配为 S × S S\times S S×S 。在这里,比较三种常见的实现方式:interpolation、adaptive-pool和region-grid-interpolation。
- Interpolation:直接双线性插值到对应的尺寸;
- Adaptive-pool:使用2D的自适应池化;
- Region-grid-interpolation:对于每个网格单元,使用以密集采样点为条件的双线性插值,并将结果与平均值相加;
根据观察,这些变体之间没有明显的性能差距(±0.1AP),这表明align过程相当灵活。
-
Different head depth: 在图5中,比较了工作中使用的不同 head depth。 将 head depth从4更改为7可获得1.2 AP增益。 图5中的结果表明,当深度超过7时,性能将变得稳定。在本文中,作者在其他实验中使用的深度为7。
![[实例分割] SOLO: Segmenting Objects by Locations 论文阅读_第11张图片](http://img.e-com-net.com/image/info8/659cafe107c64dd682f2f3857741cece.jpg)
3.2 SOLO-512
作者还训练了一个较小的SOLO版本,旨在加快推理速度。使用输入分辨率较小的模型(较短的图像尺寸为512,而不是800)。SOLO-512和SOLO之间的其他训练和测试参数相同。
![[实例分割] SOLO: Segmenting Objects by Locations 论文阅读_第12张图片](http://img.e-com-net.com/image/info8/79d9a80b88134d1a9d3c4a98ff3966af.jpg)
借助34.2% mask AP,SOLO-512的模型推断速度达到了22.5 FPS,这表明SOLO具有用于实时实例分割应用程序的潜力。在单个V100 GPU上平均5次运行获得的帧率。
4. Decoupled SOLO
给定预定义的网格编号,例如 S = 20 S = 20 S=20 ,SOLO head输出 S 2 = 400 S^2=400 S2=400 个通道图。但是,该预测有些多余,因为在大多数情况下,目标在图像中是稀疏的,因为不太可能在一幅图像中出现这么多实例。在本节中,作者进一步介绍了普通SOLO的等效且效率更高的变体,称为decoupled SOLO。如图7所示。
![[实例分割] SOLO: Segmenting Objects by Locations 论文阅读_第13张图片](http://img.e-com-net.com/image/info8/2b2f47acfc5e4faeb981f45cea6d14e2.jpg)
在 decoupled SOLO中,原始输出张量 M ∈ R H × W × S M\in R^{H\times W \times S} M∈RH×W×S 被分别对应于两个轴的两个输出张量 X ∈ R H × W × S X\in R^{H\times W \times S} X∈RH×W×S和 Y ∈ R H × W × S Y\in R^{H\times W \times S} Y∈RH×W×S代替。 因此,输出空间从 H × W × S 2 H\times W \times S^2 H×W×S2 减少到 H × W × 2 S H\times W \times 2S H×W×2S。对于位于网格位置 ( i , j ) (i,j) (i,j)的对象,vanilla SOLO在输出张量 M M M 的第 k k k 个通道上对其掩码进行分割,其中 k = i ⋅ S + j k = i\cdot S + j k=i⋅S+j。 在 decoupled SOLO中,该对象的掩模预测被定义为两个通道映射的元素乘:
![]()
其中, x j x_j xj 和 y i y_i yi是 X X X 第 j j j 通道图和 Y Y Y 第 i i i 通道图经过 sigmoid操作后的结果。
使用与普通的SOLO相同的超参数进行实验。 如表7所示,decoupled SOLO的性能与普通的SOLO相同。这表明解耦后的SOLO在SOLO精度方面可以作为等效的高效变量。请注意,由于输出空间大大减少,因此在训练和测试期间,Decoupled SOLO需要的GPU内存要少得多。
![[实例分割] SOLO: Segmenting Objects by Locations 论文阅读_第14张图片](http://img.e-com-net.com/image/info8/4d9e749bcbf94e40ac9ad387a49a0045.jpg)
5. Error Analysis
为了定量了解SOLO进行mask预测,通过将预测的mask替换为真实值来执行错误分析。对于每个预测的二进制掩码,用真实的掩码计算IoU,然后用最重叠的真实的掩码替换。如表8所示,如果将预测的mask替换为真实的mask,则AP会增加到68.1。该实验表明,仍有足够的空间来改善mask分支。
![[实例分割] SOLO: Segmenting Objects by Locations 论文阅读_第15张图片](http://img.e-com-net.com/image/info8/68de4638d3d944e58402eb8fa05bf419.jpg)
6. SOLO for Instance Contour Detection
通过更改mask分支的优化目标,SOLO 框架可以轻松扩展到实例轮廓检测。首先使用OpenCV的findContours函数将MS COCO中的真实掩码转换为实例轮廓,然后使用二进制轮廓与语义类别分支并行优化掩码分支。这里使用Focal Loss来优化轮廓检测,其他设置与实例分割基线相同。图6显示了我们的模型生成的一些轮廓检测示例。提供这些结果作为SOLO可用于轮廓检测的概念证明。
![[实例分割] SOLO: Segmenting Objects by Locations 论文阅读_第16张图片](http://img.e-com-net.com/image/info8/9d0e1cb2a4bb434eb3f3a0702a565980.jpg)