大话数据结构---（六）图的前期准备
1.图的定义与术语总结
图按照有无方向分为无向图和有向图。无向图由顶点和边构成，有向图由顶点和弧构成。弧有弧尾和弧头之分。
图按照边或弧的多少分稀疏图和稠密图。如果任意两个顶点之间都存在边叫完全图，有向的叫有向完全图。若无重复的边或顶点到自身的边则叫简单图。
图中顶点之间有邻接点、依附的概念。无向图顶点的边数叫做度，有向图顶点分为入度和出度。
图上的边或弧上带权则称为网。
图中顶点间存在路径，两顶点存在路径则说明是连通的，如果路径最终回到起始点则称为环，当中不重复叫做简单路径。若任意两顶点都是连通的，则图就是连通图，有向则称强连通图。图中有子图，若子图极大连通就是连通分量，有向则称强连通分量。
无向图中连通且n个顶点n-1条边叫生成树。有向图中一顶点入度为0其余顶点入度为1的叫有向树。一个有向图由若干棵有向树构成生成森林。
2.图的存储结构
图的存储结构相较于树的存储结构就更为复杂了，我们这里介绍五种图的存储结构，每种存储结构都有各自的优缺点。我们需要掌握的是当我们遇到一个新的问题，如何构思出适当的存储结构来解决问题。
就我个人而言，在写一个算法题时，如果涉及的要素过多，我会选择定义一个结构来存储所有信息。而现在谈到的图，它所包含的信息有顶点、边或者弧、权值。这些元素看似独立，可以全部存储在一个结构中。这里我们假设定义了一个结构AllElement里面包含了顶点、边和权值，对于一个图而言，我们会存储这个图的所有顶点，所以结构中的顶点是一个顶点数组，类似的边也会是一个边数组，权值怎么办，有人可能会说，将边和权值存储到一个新的结构Edge中，在AllElement结构中的元素就成了顶点数组和Edge结构数组。现在看来，我们确实将一个图的所有信息都存进去了，可是这个存储结构对我们 之后的操作能带来实际性的意义吗。它们只是毫无规律可循的存储在一个结构中，对之后任何操作的判定和运行都没有简化作用，所以这样的结构是失败的也是不可行的。
因此对于图来说，如何对他实现物理存储是个难题，不过我们的前辈们已经解决了，现在我们来看前辈们提供的三种不同的存储结构，重点理解他们的分析思想。
邻接矩阵：对于图而言，既然顶点和边合在一起存储比较困难，那么我们就将它们分开存储。考虑到顶点不分大小，主次且个数固定，那么我们可以用一个一维数组来存储。而边反应的是两个顶点的关系，为了反映这层关系（即将两个顶点表示出来的同时，并说明这两个顶点之间有无边），一维无法搞定，那么我们就用二维数组存储。这样，邻接矩阵的存储结构就分析出来了。
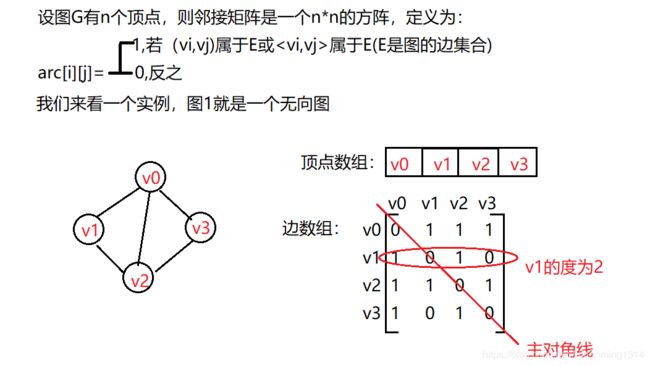这里对上图进行说明，我们设置两个数组，顶点数组vertext[4]={v0,v1,v2,v3},边二维数组arc。arc中（0,1）=1是因为v0到v1的边存在，而（1,3）=0是因为v1到v3的边不存在。有了这个矩阵，我们就可以很容易地知道图中的信息。
- 判定两个顶点有无边就很容易
- 要想知道某个顶点的度，只需遍历该点所在的行或列的元素值之和，比如顶点v1的度之和为1+0+1+0=2。
- 求某个顶点的所有邻接点就是该点所在的行或列元素值为1的的点，比如v1的邻接点有v0,v2。
不难发现，对于无向图而言，它的邻接矩阵是对称矩阵，那么可以想象有向图的邻接矩阵，下面我们再来看一个有向样例。
在图的术语中，我们提到了网的概念，也就是每条边上带有权的图叫做网。那么这些权值就需要存下来，我们看看上图，邻接矩阵中的值1或0，它们只是表示边的存在与不存在，值本身并无实际意义，那么我们就可以利用这些值，也就是网内各边的权值。
那么邻接矩阵是如何实现图的创建的呢，我们先来看看图的邻接矩阵存储的结构
typedef char VertextType;//顶点类型应由用户定义
typedef int EdgeType;//边上的权值类型应由用户定义
#define MAXVEX 100 //最大顶点数，应由用户定义
#define INFINITY 65535//用65535来代表无穷
typedef struct {
VertextType vexs[MAXVEX];//顶点表
EdgeType arc[MAXVEX][MAXVEX];//邻接矩阵，可看作边表
int numVertexes, numEdges;//图中当前的顶点数和边数
}MGraph;
有了这个结构定义，我们构造一个图，其实就是给顶点表和边表输入数据的过程，我们来看看无向网图的创建代码。
//建立无向网图的邻接矩阵表示
void CreateMGraph(MGraph *G) {
int i, j, k, w;
cout << "输入顶点数和边数：" << endl;
cin >> G->numVertexes >> G->numEdges;//输入顶点数和边数
for (i = 0; i < G->numVertexes; i++) {//读入顶点信息，建立顶点表
cin >> G->vexs[i];
}
for (i = 0; i < G->numVertexes; i++) {
for (j = 0; j < G->numVertexes; i++) {
G->arc[i][j] = INFINITY;//邻接矩阵初始化
}
}
for (k = 0; k < G->numEdges; k++) {
cout << "输入边(vi,vj)上的下标i,下标j和权w:" << endl;
cin >> i >> j >> w;
G->arc[i][j] = w;
G->arc[j][i] = w;//无向图，矩阵对称
}
}
邻接表：邻接矩阵确实通过比较简单的方式存储了图的所有信息，而且能反映出图的一些性质，但有个缺点就是内存使用率的问题。如果一个图顶点个数较多，边个数较少。那么它同样需要分配很大的内存空间，只有少量部分存储该图的边，其余部分都被用来说明“没有边”这一概念了。既然直接分配固定内存会导致空间浪费，自然而然会想到链式结构。在上一章树中，我们导论到树的表示法有一种孩子表示法：树的各个结点用一维数组存储，各结点的孩子结点用链表存储，这一方法同样适用图的存储。我们把这种数组与链表相结合的存储方法称为邻接表，如图3所示就是一个无向图的邻接表结构。
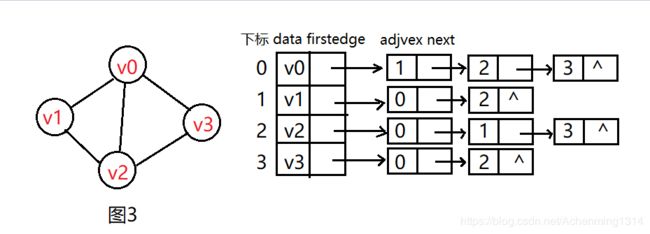由图我们可知，顶点表的各个结点由data和firstedge两个域表示。data是数据域，存储顶点的信息，firstedge是指针域，指向边表的第一个结点。边表结点由adjvex和next两个域表示。adjvex是邻接点域，存储某顶点的邻接点在顶点表中的小标，next则存储指向边表中下一个结点的指针。
从邻接表中我们很容易就可以计算出某个顶点的入度或出度是多少，判断两顶点是否存在弧也很容易实现。对于带权值的网图，可以在边表结点定义中再增加一个weight的数据域，存储权值信息即可，有了这些结构的图，下面关于结点定义的代码就很好理解了。
#define MAXVEX 100
typedef char VertextType;//顶点类型应由用户定义
typedef int EdgeType;//边上的权值类型应由用户定义
typedef struct EdgeNode {//边表结点
int adjvex;//邻接点域，存储该顶点对应的下标
EdgeType weight;//用于存储权值，对于非网图可以不需要
struct EdgeNode *next;//链域，指向下一个邻接点
}EdgeNode;
typedef struct VertextNode {//顶点表结点
VertextType data;//顶点域，存储顶点信息
EdgeNode *firstedge;//边表头指针
}VertexNode,AdjList[MAXVEX];
typedef struct {
AdjList adjList;
int numVertexes, numEdges;//图中当前顶点数和边数
}GraphAdjList;
对于邻接表的创建，也就是顺理成章之事。无向图的邻接表创建代码如下：
void CreateALGraph(GraphAdjList *G) {
int i, j, k;
EdgeNode *e;
cout << "输入顶点数和边数：" << endl;
cin >> G->numVertexes >> G->numEdges;//输入顶点数和边数
for (i = 0; i < G->numVertexes; i++) {
cin >> G->adjList[i].data;//输入顶点信息
G->adjList[i].firstedge = NULL;//将边表置为空表
}
for (k = 0; k < G->numEdges; k++) {//建立边表
cout << "输入边(vi,vj)上的顶点序号：" << endl;
cin >> i >> j;//输入边(vi,vj)上的顶点序号
e = (EdgeNode *)malloc(sizeof(EdgeNode));//向内存申请空间，生成边表结点
e->adjvex = j;//邻接序号为j
e->next = G->adjList[i].firstedge;//将e指针指向当前顶点指向的结点
G->adjList[i].firstedge = e;//将当前顶点的指针指向e--------头插法
e = (EdgeNode *)malloc(sizeof(EdgeNode));//向内存申请空间，生成边表结点
e->adjvex = i;//邻接序号为i
e->next = G->adjList[j].firstedge;//将e指针指向当前顶点指向的结点
G->adjList[j].firstedge = e;//将当前顶点的指针指向e
}
}
十字链表：对于有向图来说，邻接表是有缺陷的。关心了出度的问题，想了解入度必须遍历整个图才能知道。有没有可能把邻接表与逆邻接表结合起来呢。这就是我们现在要讲的有向图的一种存储方法：十字链表。重新定义顶点表节点结构如表所示。
firstin表示入边表头指针，指向该顶点的入边表中第一个结点，firstout表示出边表头指针，指向该顶点的出边表中的第一个结点。重新定义的边表结点结构如表所示。
tailvex是指弧起点在顶点表的下标，headvex是指弧终点在顶点表中的下标，headlink是指入边表指针域，指向终点相同的下一条边，taillink是指边表指针域，指向起点相同的下一条边，如果是网，还可以再增加一个weight域来存储权值。可能有点难理解，别着急，下面会通过一个实例，详细说明，如图4所示。
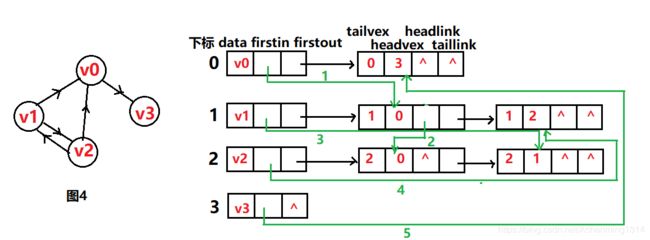这里我们一一解释，tailvex的值其实就是所在行的顶点下标，暂时忽略绿线，其实就是邻接表，黑色的线指向的结点是该顶点的出度。十字链表和邻接表的区别主要在于多了这些绿线，在分析绿线之前，我们先按邻接表的思路分析该图的黑线（出度）以及taillink，暂时忽略headlink，这是入度。
- 第一行，顶点是v0，由图可知，指向的是v3，所以firstout指向的下一个结点的headvex为3，tailvex为该顶点本身，由于v0的出度中只有v3所以taillink为“^”。
- 第二行，顶点是v1,由图可知，指向v0,v2,所以firstout指向下一个结点的headvex为0（当然也可以是2，顺序无关紧要），tailvex为该顶点本身，由于v0的出度中，除了v0还有v2，所以该结点的taillink指向的下一个结点的headvex为2，且headvex为2的结点，它的taillink为“^”。
- 第三行，顶点是v2,由图可知，指向的是v0,v1,所以firstout指向下一个结点的headvex为0（也可以是1），tailvex为该顶点本身，由于v2的出度中，除了v0还有v1,所以该结点的taillink指向的下一个结点的headvex为1，且headvex为1的结点，它的taillink为“^”。
- 第四行，顶点是v3，由图可知，并没有指向任何结点，所以该顶点的firstout指向“^”。
分析完黑线之后（出度），下面继续分析绿线（入度）。 - 第一行，顶点是v0,由图可知，顶点v1,v2指向v0,这里找到指向v0的边，即第二行第二个结点，那么将该顶点的firstin指向该结点（如绿色的1所示），除了该结点，还有第三行的第二个结点，所以将第二行第二个几点指向该结点（如绿色的2所示），并将该结点的headlink指向“^”。
- 第二行，顶点是v1,由图可知，顶点v2指向v1,这里找到指向v1的边，即第三行第三个结点，那么将该顶点的firstin指向该结点（如绿色的3所示）并将该结点的headlink指向“^”。
- 第三行，顶点是v2,由图可知，顶点v1指向v2,这里找到指向v2的边，即第二行第三个结点（如绿色的4所示），并将该结点的headlink指向“^”。
- 第四行，顶点是v3,由图可知，顶点v0,指向v3,这里找到指向v3的边，即第一行第二个结点（如绿色的5所示），并将该结点的headlink指向“^”。
终于说完了。。。呼！十字链表的好处就是因为把邻接表和逆邻接表整合在了一起，创建图算法的时间复杂度是和邻接表相同的，因此，在有向图的应用中，十字链表是非常好的数据结构模型。