「面试必问」leetcode高频题精选

引言（文末有福利）????

算法一直是大厂前端面试常问的一块，而大家往往准备这方面的面试都是通过leetcode刷题。

我特地整理了几道leetcode中「很有意思」而且非常「高频」的算法题目，分别给出了思路分析（带图解）和代码实现。

认真仔细的阅读完本文，相信对于你在算法方面的面试一定会有不小的帮助！????

两数之和 ????

❝

题目难度easy，涉及到的算法知识有数组、哈希表

❞

题目描述

给定一个整数数组 nums  和一个目标值 target，请你在该数组中找出和为目标值的那两个整数，并返回他们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素不能使用两遍。

示例：

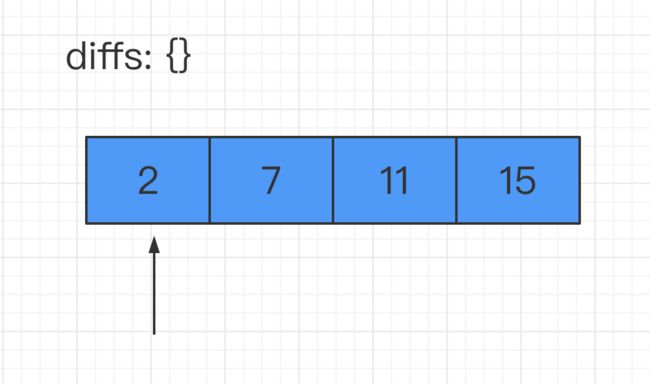
给定 nums = [2, 7, 11, 15], target = 9

因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]

思路分析

大多数同学看到这道题目，心中肯定会想：这道题目太简单了，不就两层遍历嘛：两层循环来遍历同一个数组；第一层循环遍历的值记为a，第二层循环时遍历的值记为b；若a+b = 目标值，那么a和b对应的数组下标就是我们想要的答案。

这种解法没毛病，但有没有优化的方案呢？????

要知道两层循环很多情况下都意味着O(n^2) 的复杂度，这个复杂度非常容易导致你的算法超时。即便没有超时，在明明有一层遍历解法的情况下，你写了两层遍历，面试官也会对你的印象分大打折扣。????

其实我们可以在遍历数组的过程中，增加一个Map结构来存储已经遍历过的数字及其对应的索引值。然后每遍历到一个新数字的时候，都回到Map里去查询targetNum与该数的差值是否已经在前面的数字中出现过了。若出现过，那么答案已然显现，我们就不必再往下走了。

我们就以本题中的例子结合图片来说明一下上面提到的这种思路：

• 这里用对象diffs来模拟map结构：首先遍历数组第一个元素，此时key为 2，value为索引 0

• 往下遍历，遇到了 7:计算targetNum和 7 的差值为 2，去diffs中检索 2 这个key，发现是之前出现过的值。那么本题的答案就出来了！

代码实现

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number[]}
 */
const twoSum = function (nums, target) {
  const diffs = {};
  // 缓存数组长度
  const len = nums.length;
  // 遍历数组
  for (let i = 0; i < len; i++) {
    // 判断当前值对应的 target 差值是否存在
    if (diffs[target - nums[i]] !== undefined) {
      // 若有对应差值，那么得到答案
      return [diffs[target - nums[i]], i];
    }
    // 若没有对应差值，则记录当前值
    diffs[nums[i]] = i;
  }
};

三数之和 ????

❝

题目难度medium，涉及到的算法知识有数组、双指针

❞

题目描述

给你一个包含n个整数的数组nums，判断nums中是否存在三个元素a，b，c ，使得a + b + c = 0。请你找出所有满足条件且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例：

给定数组 nums = [-1, 0, 1, 2, -1, -4]，

满足要求的三元组集合为：
[
  [-1, 0, 1],
  [-1, -1, 2]
]

思路分析

和上面的两数之和一样，如果不认真思考，最快的方式可能就是多层遍历了。但有了前车之鉴，我们同样可以把求和问题变为求差问题：固定其中一个数，在剩下的数中寻找是否有两个数的和这个固定数相加是等于 0 的。

这里我们采用双指针法来解决问题，相比三层循环，效率会大大提升。

❝

双指针法的适用范围比较广，一般像求和、比大小的都可以用它来解决。但是有一个前提：数组必须有序

❞

因此我们的第一步就是先将数组进行排序：

// 给 nums 排序
nums = nums.sort((a,b)=>{
    return a-b
})

然后对数组进行遍历，每遍历到哪个数字，就固定当前的数字。同时左指针指向该数字后面的紧邻的那个数字，右指针指向数组末尾。然后左右指针分别向中间靠拢：每次指针移动一次位置，就计算一下两个指针指向数字之和加上固定的那个数之后，是否等于 0。如果是，那么我们就得到了一个目标组合；否则，分两种情况来看：

• 相加之和大于 0，说明右侧的数偏大了，右指针左移

• 相加之和小于 0，说明左侧的数偏小了，左指针右移

代码实现

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
const threeSum = function(nums) {
    // 用于存放结果数组
    let res = []
    // 目标值为0
    let sum = 0
    // 给 nums 排序
    nums = nums.sort((a,b)=>{
        return a-b
    })
    // 缓存数组长度
    const len = nums.length
    for(let i=0;i0&&nums[i]===nums[i-1]) {
            continue
        }
        while(j0){
                // 三数之和大于0，右指针后退
                k--

               // 处理右指针元素重复的情况
               while(j

盛最多水的容器 ????

❝

题目难度medium，涉及到的算法知识有数组、双指针

❞

题目描述

给你 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点  (i, ai) 。在坐标内画 n 条垂直线，垂直线 i  的两个端点分别为  (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与  x  轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且  n  的值至少为 2。图中垂直线代表输入数组[1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例：

输入：[1,8,6,2,5,4,8,3,7]
输出：49

思路分析

首先，我们能快速想到的一种方法：两两进行求解，计算可以承载的水量。 然后不断更新最大值，最后返回最大值即可。

这种解法，需要两层循环，时间复杂度是O(n^2)。这种相对来说比较暴力，对应就是暴力法。

暴力法

/**
 * @param {number[]} height
 * @return {number}
 */
var maxArea = function(height) {
    let max = 0;
    for(let i = 0; i< height.length-1; i++) {
        for(let j = i + 1; j < height.length;j++) {
            let area = (j - i) * Math.min(height[i], height[j]);
            max = Math.max(max, area)
        }
    }

    return max;
}

那么有没有更好的办法呢？答案是肯定有。

其实有点类似双指针的概念，左指针指向下标 0，右指针指向length-1。然后分别从左右两侧向中间移动，每次取小的那个值（因为水的高度肯定是以小的那个为准）。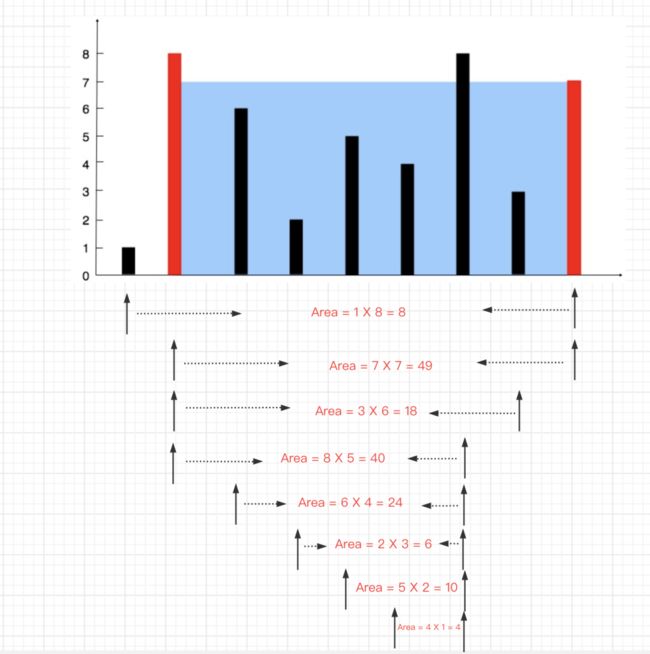

如果左侧小于右侧，则i++，否则j--（这一步其实就是取所有高度中比较高的，我们知道面积等于长*宽）。对应就是双指针 动态滑窗

双指针 动态滑窗

/**
 * @param {number[]} height
 * @return {number}
 */
var maxArea = function(height) {
    let max = 0;
    let i = 0;
    let j = height.length - 1;
    while(i < j) {
        let minHeight = Math.min(height[i], height[j])
        let area = (j - i)*minHeight;
        max = Math.max(max, area)
        if(height[i] < height[j]) {
            i++
        } else {
            j--
        }
    }
    return max
};

爬楼梯 ????

❝

题目难度easy，涉及到的算法知识有斐波那契数列、动态规划。

❞

题目描述

假设你正在爬楼梯。需要 n  阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶

示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

思路分析

这道题目是一道非常高频的面试题目，也是一道非常经典的斐波那契数列类型的题目。

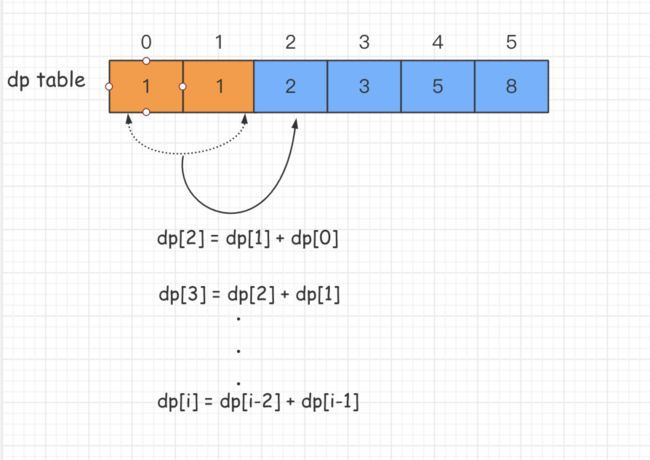
解决本道题目我们会用到动态规划的算法思想-可以分成多个子问题，爬第 n 阶楼梯的方法数量，等于 2 部分之和：

• 爬上n−1阶楼梯的方法数量。因为再爬 1 阶就能到第 n 阶

• 爬上n−2阶楼梯的方法数量，因为再爬 2 阶就能到第 n 阶

可以得到公式：

climbs[n] = climbs[n-1] + climbs[n-2]

同时需要做如下初始化：

climbs[0] = 1;
climbs[1] = 1

代码实现

/**
 * @param {number} n
 * @return {number}
 */
var climbStairs = function(n) {
    let climbs = [];
    climbs[0] = 1;
    climbs[1] = 1;
    for(let i = 2; i<= n; i++) {
        climbs[i] = climbs[i-1] + climbs[i-2]
    }
    return climbs[n]

};

环形链表 ????

❝

题目难度easy，涉及到的算法知识有链表、快慢指针。

❞

题目描述

给定一个链表，判断链表中是否有环。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

思路分析

链表成环问题也是非常经典的算法问题，在面试中也经常会遇到。

解决这种问题一般有常见的两种方法：标志法和快慢指针法。

标志法

给每个已遍历过的节点加标志位，遍历链表，当出现下一个节点已被标志时，则证明单链表有环。

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */

/**
 * @param {ListNode} head
 * @return {boolean}
 */
var hasCycle = function(head) {
    while(head) {
        if(head.flag) return true
        head.flag = true;
        head = head.next;
    }
    return false
};

快慢指针（双指针法）

设置快慢两个指针，遍历单链表，快指针一次走两步，慢指针一次走一步，如果单链表中存在环，则快慢指针终会指向同一个节点，否则直到快指针指向null时，快慢指针都不可能相遇。

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */

/**
 * @param {ListNode} head
 * @return {boolean}
 */
var hasCycle = function(head) {
    if(!head || !head.next) {
        return false
    }
    let slow = head, fast = head.next;
    while(slow !== fast) {
        if(!fast || !fast.next) return false
        fast = fast.next.next;
        slow = slow.next
    }
    return true;
};

有效的括号 ????

❝

题目难度easy，涉及到的算法知识有栈、哈希表。

❞

题目描述

给定一个只包括'('，')'，'{'，'}'，'['，']'  的字符串，判断字符串是否有效。

有效字符串需满足：

1、左括号必须用相同类型的右括号闭合。 2、左括号必须以正确的顺序闭合。

注意空字符串可被认为是有效字符串。

示例 1:

输入: "()"
输出: true

示例  2:

输入: "()[]{}"
输出: true

示例  3:

输入: "(]"
输出: false

示例  4:

输入: "([)]"
输出: false

示例  5:

输入: "{[]}"
输出: true

思路分析

这道题可以利用栈结构。

思路大概是：遇到左括号，一律推入栈中，遇到右括号，将栈顶部元素拿出，如果不匹配则返回 false，如果匹配则继续循环。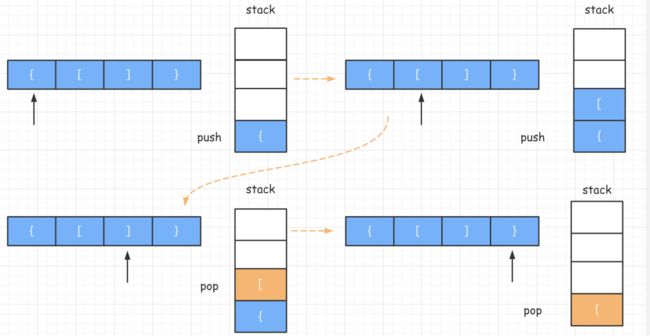第一种解法是利用switch case。

switch case

/**
 * @param {string} s
 * @return {boolean}
 */
var isValid = function(s) {
    let arr = [];
    let len = s.length;
    if(len%2 !== 0) return false
    for(let i = 0; i

第二种是维护一个map对象：

哈希表map

/**
 * @param {string} s
 * @return {boolean}
 */
var isValid = function(s) {
    let map = {
        '(': ')',
        '{': '}',
        '[': ']'
    }
    let stack = [];
    let len = s.length;
    if(len%2 !== 0) return false
    for(let i of s) {
        if(i in map) {
            stack.push(i)
        }  else {
            if(i !== map[stack.pop()]) return false
        }
    }
    return !stack.length
};

滑动窗口最大值 ⛵

❝

题目难度hard，涉及到的算法知识有双端队列。

❞

题目描述

给定一个数组 nums，有一个大小为  k  的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k  个数字。滑动窗口每次只向右移动一位。

返回滑动窗口中的最大值。

进阶：你能在线性时间复杂度内解决此题吗？

示例:

输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释:

  滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

提示：

• 1 <= nums.length <= 10^5

• -10^4 <= nums[i] <= 10^4

• 1 <= k <= nums.length

思路分析

暴力求解

第一种方法，比较简单。也是大多数同学很快就能想到的方法。

• 遍历数组

• 依次遍历每个区间内的最大值，放入数组中

/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number[]}
 */
var maxSlidingWindow = function(nums, k) {
    let len = nums.length;
    if(len === 0) return []
    if(k === 1) return nums
    let resArr = []
    for(let i = 0; i <= len - k;i++) {
        let max = Number.MIN_SAFE_INTEGER;
        for(let j = i; j < i + k; j++) {
            max = Math.max(max, nums[j])
        }
        resArr.push(max)
    }
    return resArr;
};

双端队列

这道题还可以用双端队列去解决，核心在于在窗口发生移动时，只根据发生变化的元素对最大值进行更新。

结合上面动图(图片来源)我们梳理下思路：

• 检查队尾元素，看是不是都满足大于等于当前元素的条件。如果是的话，直接将当前元素入队。否则，将队尾元素逐个出队、直到队尾元素大于等于当前元素为止。（这一步是为了维持队列的递减性：确保队头元素是当前滑动窗口的最大值。这样我们每次取最大值时，直接取队头元素即可。）

• 将当前元素入队

• 检查队头元素，看队头元素是否已经被排除在滑动窗口的范围之外了。如果是，则将队头元素出队。（这一步是维持队列的有效性：确保队列里所有的元素都在滑动窗口圈定的范围以内。）

• 排除掉滑动窗口还没有初始化完成、第一个最大值还没有出现的特殊情况。

/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number[]}
 */
var maxSlidingWindow = function(nums, k) {
    // 缓存数组的长度
    const len = nums.length;
    const res = [];
    const deque = [];
    for (let i = 0; i < len; i++) {
        // 队尾元素小于当前元素
        while (deque.length && nums[deque[deque.length - 1]] < nums[i]) {
            deque.pop()
        }
        deque.push(i)

        // 当队头元素的索引已经被排除在滑动窗口之外时
        while (deque.length && deque[0] <= i - k) {
            // 队头元素出对
            deque.shift()
        }
        if (i >= k - 1) {
            res.push(nums[deque[0]])
        }
    }
    return res
};

每日温度 ????

❝

题目难度medium，涉及到的算法知识有栈。

❞

题目描述

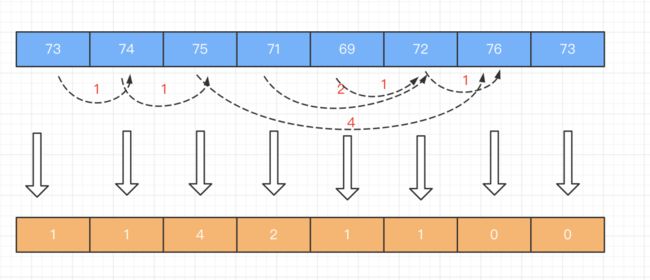
根据每日气温列表，请重新生成一个列表，对应位置的输出是需要再等待多久温度才会升高超过该日的天数。如果之后都不会升高，请在该位置用  0 来代替。

例如，给定一个列表  temperatures = [73, 74, 75, 71, 69, 72, 76, 73]，你的输出应该是  [1, 1, 4, 2, 1, 1, 0, 0]。

提示：气温列表长度的范围是  [1, 30000]。每个气温的值的均为华氏度，都是在  [30, 100]  范围内的整数。

思路分析

看到这道题，大家很容易就会想到暴力遍历法：直接两层遍历，第一层定位一个温度，第二层定位离这个温度最近的一次升温是哪天，然后求出两个温度对应索引的差值即可。

然而这种解法需要两层遍历，时间复杂度是O(n^2)，显然不是最优解法。

本道题目可以采用栈去做一个优化。

大概思路就是：维护一个递减栈。当遍历过的温度，维持的是一个单调递减的态势时，我们就对这些温度的索引下标执行入栈操作；只要出现了一个数字，它打破了这种单调递减的趋势，也就是说它比前一个温度值高，这时我们就对前后两个温度的索引下标求差，得出前一个温度距离第一次升温的目标差值。

代码实现

/**
 * @param {number[]} T
 * @return {number[]}
 */
var dailyTemperatures = function(T) {
    const len = T.length;
    const stack = [];
    const res = (new Array(len)).fill(0);
    for (let i=0; i < len;i++) {
        while(stack.length && T[i] > T[stack[stack.length - 1]]) {
            const top = stack.pop();
            res[top] = i - top;
        }
        stack.push(i)
    }
    return res
};

括号生成 ????

❝

题目难度medium，涉及到的算法知识有递归、回溯。

❞

题目描述

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例：

输入：n = 3
输出：[
       "((()))",
       "(()())",
       "(())()",
       "()(())",
       "()()()"
     ]

思路分析

这道题目通过递归去实现。

因为左右括号需要匹配、闭合。所以对应“(”和“)”的数量都是n，当满足这个条件时，一次递归就结束，将对应值放入结果数组中。

这里有一个潜在的限制条件：有效的括号组合。对应逻辑就是在往每个位置去放入“(”或“)”前：

• 需要判断“(”的数量是否小于 n

• “)”的数量是否小于“(”

代码实现

/**
 * @param {number} n
 * @return {string[]}
 */
var generateParenthesis = function(n) {
    let res = []
    const generate = (cur, left, right) => {
        if (left ===n && right === n) {
            res.push(cur)
            return
        }
        if (left < n) {
            generate(cur + '(', left + 1, right)
        }
        if (right < left) {
            generate(cur + ')', left, right + 1)
        }
    }
    generate('', 0, 0)
    return res
};

电话号码的字母组合 ????

❝

题目难度medium，涉及到的算法知识有递归、回溯。

❞

题目描述

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。示例:

输入："23"
输出：["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].

思路分析

首先用一个对象map存储数字与字母的映射关系，接下来遍历对应的字符串，第一次将字符串存在结果数组result中，第二次及以后的就双层遍历生成新的字符串数组。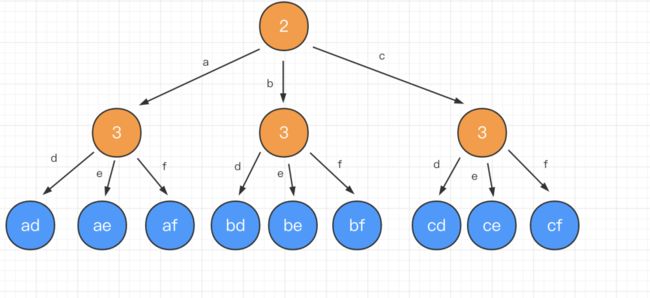

代码实现

哈希映射 逐层遍历

/**
 * @param {string} digits
 * @return {string[]}
 */
var letterCombinations = function(digits) {
    let res = [];
    if (digits.length === 0) return []
    let map = {
        2: 'abc',
        3: 'def',
        4: 'ghi',
        5: 'jkl',
        6: 'mno',
        7: 'pqrs',
        8: 'tuv',
        9: 'wxyz'
    }
    for (let num of digits) {
        let chars = map[num]
        if (res.length > 0) {
            let temp = []
            for (let char of chars) {
                for (let oldStr of res) {
                    temp.push(oldStr + char)
                }
            }
            res = temp
        } else {
            res.push(...chars)
        }

    }
    return res
};

递归

/**
 * @param {string} digits
 * @return {string[]}
 */
var letterCombinations = function(digits) {
    let res = [];
    if (!digits) return []
    let map = {
        2: 'abc',
        3: 'def',
        4: 'ghi',
        5: 'jkl',
        6: 'mno',
        7: 'pqrs',
        8: 'tuv',
        9: 'wxyz'
    }
    function generate(i, str) {
        let len = digits.length;
        if (i === len) {
            res.push(str)
            return
        }
        let chars = map[digits[i]]
        for (let j = 0; j < chars.length; j++) {
            generate(i+1, str + chars[j])
        }
    }
    generate(0, '')
    return res
};

岛屿数量 ????

❝

题目难度medium，涉及到的算法知识有 DFS（深度优先搜索）。

❞

题目描述

给你一个由  '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1:

输入:
11110
11010
11000
00000
输出: 1

示例  2:

输入:
11000
11000
00100
00011
输出: 3
解释: 每座岛屿只能由水平和/或竖直方向上相邻的陆地连接而成。

思路分析

如上图，我们需要计算的就是图中相连（只能是水平和/或竖直方向上相邻）的绿色岛屿的数量。

这道题目一个经典的做法是沉岛，大致思路是：采用DFS（深度优先搜索），遇到 1 的就将当前的 1 变为 0，并将当前坐标的上下左右都执行 dfs，并计数。

终止条件是：超出二维数组的边界或者是遇到 0 ，直接返回。

代码实现

/**
 * @param {character[][]} grid
 * @return {number}
 */
var numIslands = function(grid) {
    const rows = grid.length;
    if (rows === 0) return 0
    const cols = grid[0].length;
    let res = 0;
    for (let i = 0; i < rows; i++) {
        for (let j = 0; j < cols; j++) {
            if (grid[i][j] === '1') {
                helper(grid, i, j, rows, cols)
                res++
            }
        }
    }
    return res
}
 function helper(grid, i, j, rows, cols) {
    if (i < 0 || j < 0 || i > rows - 1 || j > cols - 1 || grid[i][j] === "0")
        return;

    grid[i][j] = "0"

    helper(grid, i + 1, j, rows, cols);
    helper(grid, i, j + 1, rows, cols);
    helper(grid, i - 1, j, rows, cols);
    helper(grid, i, j - 1, rows, cols);

}

分发饼干 ????

❝

题目难度easy，涉及到的算法知识有贪心算法。

❞

题目描述

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。对每个孩子 i ，都有一个胃口值  gi ，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j ，都有一个尺寸 sj 。如果 sj >= gi ，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

注意：

你可以假设胃口值为正。 一个小朋友最多只能拥有一块饼干。

示例  1:

输入: [1,2,3], [1,1]

输出: 1

解释:
你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。

示例  2:

输入: [1,2], [1,2,3]

输出: 2

解释:
你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.

思路分析

这道题目是一道典型的贪心算法类。解题思路大概如下：

• 优先满足胃口小的小朋友的需求

• 设最大可满足的孩子数量为maxNum = 0

• 胃口小的拿小的，胃口大的拿大的

• 两边升序，然后一一对比

• 当饼干j >= 胃口i 时，i++、j++、maxNum++

• 当饼干j < 胃口i时，说明饼干不够吃，换更大的，j++

• 到边界后停止

代码实现

/**
 * @param {number[]} g
 * @param {number[]} s
 * @return {number}
 */
var findContentChildren = function(g, s) {
    g = g.sort((a, b) => a - b)
    s = s.sort((a, b) => a - b)
    let gLen = g.length,
        sLen = s.length,
        i = 0,
        j = 0,
        maxNum = 0;
    while (i < gLen && j < sLen) {
        if (s[j] >= g[i]) {
            i++;
            maxNum++
        }
        j++
    }
    return maxNum
};

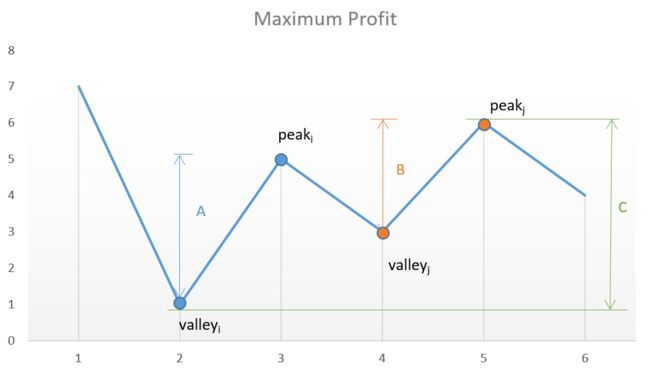
买卖股票的最佳时机 II ????

❝

题目难度easy，涉及到的算法知识有动态规划、贪心算法。

❞

题目描述

给定一个数组，它的第  i 个元素是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
     随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

示例 2:

输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
     注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。
     因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例  3:

输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

提示：

• 1 <= prices.length <= 3 * 10 ^ 4

• 0 <= prices[i] <= 10 ^ 4

思路分析

其实这道题目思路也比较简单：

• 维护一个变量profit用来存储利润

• 因为可以多次买卖，那么就要后面的价格比前面的大，那么就可以进行买卖

• 因此，只要prices[i+1] > prices[i]，那么就去叠加profit

• 遍历完成得到的profit就是获取的最大利润

代码实现

/**
 * @param {number[]} prices
 * @return {number}
 */
var maxProfit = function(prices) {
    let profit = 0;
    for (let i=0; i < prices.length - 1; i++) {
        if (prices[i+1] > prices[i]) profit += prices[i+1] - prices[i]
    }
    return profit
};

不同路径 ????

❝

题目难度medium，涉及到的算法知识有动态规划。

❞

题目描述

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？例如，上图是一个 7 x 3 的网格。有多少可能的路径？

示例  1:

输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

示例  2:

输入: m = 7, n = 3
输出: 28

思路分析

由题可知：机器人只能向右或向下移动一步，那么从左上角到右下角的走法 = 从右边开始走的路径总数+从下边开始走的路径总数。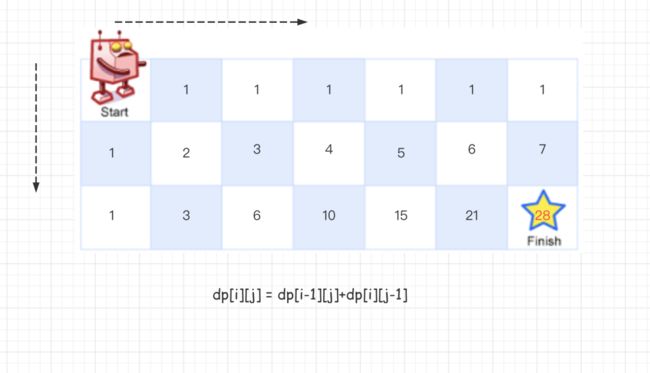

所以可推出动态方程为：dp[i][j] = dp[i-1][j]+dp[i][j-1]。

代码实现

❝

这里采用Array(m).fill(Array(n).fill(1))进行了初始化，因为每一格至少有一种走法。

❞

/**
 * @param {number} m
 * @param {number} n
 * @return {number}
 */
var uniquePaths = function(m, n) {
    let dp = Array(m).fill(Array(n).fill(1))
    for (let i = 1; i < m;i++) {
        for (let j = 1; j< n; j++) {
            dp[i][j] = dp[i-1][j] + dp[i][j-1]
        }
    }
    return dp[m-1][n-1]

};

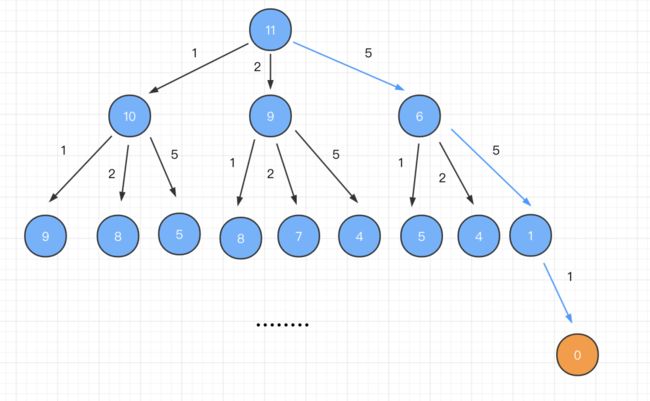
零钱兑换 ????

❝

题目难度medium，涉及到的算法知识有动态规划。

❞

题目描述

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回  -1。

示例  1:

输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1

示例 2:

输入: coins = [2], amount = 3
输出: -1

说明:你可以认为每种硬币的数量是无限的。

思路分析

这道题目我们同样采用动态规划来解决。

假设给出的不同面额的硬币是[1, 2, 5]，目标是 60，问最少需要的硬币个数？

我们需要先分解子问题，分层级找最优子结构。

❝

dp[i]: 表示总金额为 i 的时候最优解法的硬币数

❞

我们想一下：求总金额 60 有几种方法？一共有 3 种方式，因为我们有 3 种不同面值的硬币。

• 拿一枚面值为 1 的硬币 + 总金额为 59 的最优解法的硬币数量。即：dp[59] + 1

• 拿一枚面值为 2 的硬币 + 总金额为 58 的最优解法的硬币数。即：dp[58] + 1

• 拿一枚面值为 5 的硬币 + 总金额为 55 的最优解法的硬币数。即：dp[55] + 1

所以，总金额为 60 的最优解法就是上面这三种解法中最优的一种，也就是硬币数最少的一种，我们下面用代码来表示一下：

dp[60] = Math.min(dp[59] + 1, dp[58] + 1, dp[55] + 1);

推导出状态转移方程：

dp[i] = Math.min(dp[i - coin] + 1, dp[i - coin] + 1, ...)

❝

其中 coin 有多少种可能，我们就需要比较多少次，遍历 coins 数组，分别去对比即可

❞

代码实现

/**
 * @param {number[]} coins
 * @param {number} amount
 * @return {number}
 */
var coinChange = function(coins, amount) {
    let dp = new Array(amount+1).fill(Infinity)
    dp[0] = 0;
    for (let i=0;i<= amount;i++) {
        for (let coin of coins) {
            if (i - coin >= 0) {
                dp[i] = Math.min(dp[i], dp[i-coin]+1)
            }
        }
    }
    return dp[amount] === Infinity ? -1 : dp[amount]
};

福利

大多数前端同学对于算法的系统学习，其实是比较茫然的，这里我整理了一张思维导图，算是比较全面的概括了前端算法体系。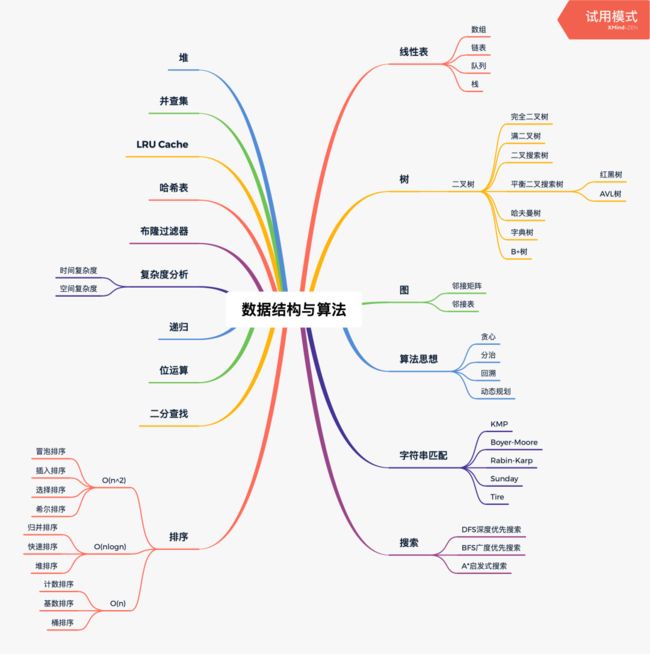

另外我还维护了一个github仓库：https://github.com/Jack-cool/js_algorithm，里面包含了大量的leetcode题解，并且还在不断更新中，感觉不错的给个star哈！????