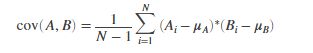【 MATLAB 】协方差 cov以及协方差矩阵基础知识

Covariance 翻译为协方差，因此，MATLAB里面的函数cov也就是求协方差了。至于MATLAB语言里面的协方差函数cov的语法是什么样的以及怎么用的，我们稍后再说，这里首先介绍下协方差相关的基础知识点。

本文内容参考自MATLAB的帮助手册，有的时候不得不说，数据手册才是最好的教材，不仅对于MATLAB，这里提供的都是原滋原味的官方内容。例如我经常去了解一些MATLAB中的相关函数，命令等，都可以通过MATLAB的数据手册；如果我想了解一些IP核以及与之相关的知识，我可以查看Xilinx的官方数据手册，内容应有尽有，相比而言，如果我去借一些书籍去查看FPGA的IP核，不仅版本陈旧，而已也有可能翻译的有问题，让人一知半解。

废话就说到这里，下面正式开始介绍。

---

---

目录

基础知识

协方差（Covariance）：

协方差矩阵（ covariance matrix）：

矩阵的协方差：

方差：（这是赠送的）

MATLAB中的 cov

语法格式：

C = cov(A)

C = cov(A,B) 

C = cov(___,w)

C = cov(___,nanflag)

示例

C = cov(A) 举例（矩阵的协方差）

cov(A,B) 举例之两个向量之间的协方差

cov(A,B) 举例之两个矩阵之间的协方差

Specify Normalization Weight

Covariance Excluding NaN

---

---

---

基础知识

协方差（Covariance）：

对于两个随机变量向量A和B，那二者之间的协方差定义为：

其中表示向量A的均值，表示向量B的均值。

协方差矩阵（ covariance matrix）：

两个随机变量的协方差矩阵是每个变量之间成对协方差计算的矩阵，

矩阵的协方差：

对于矩阵A，其列各自是由观察组成的随机变量，协方差矩阵是每个列组合之间的成对协方差计算。 换一种说法

方差：（这是赠送的）

对于由N个标量观测组成的随机变量向量A，方差定义为

其中u是A的均值：

一些方差定义使用归一化因子N而不是N-1，可以通过将w设置为1来指定。在任何一种情况下，假设均值具有通常的归一化因子N.

（注意：w是后面要说的MATLAB里面的协方差函数的一个参数而已，在具体的MATLAB函数里面可以通过设置w来指定归一化因子！）

---

---

MATLAB中的 cov

语法格式：

下面逐个讲解：

C = cov(A)

C = cov(A) returns the covariance.

C = cov(A)返回协方差。

• If A is a vector of observations, C is the scalar-valued variance.

• 如果A是一个观测向量，那么C是一个标量值的方差。

• If A is a matrix whose columns represent random variables and whose rows represent observations, C is the covariance matrix with the corresponding column variances along the diagonal.

• 如果A是矩阵，其列表示随机变量，其行表示观测值，则C是协方差矩阵，沿对角线具有相应的列方差。（协方差矩阵的协方差是列的协方差值）

• C is normalized by the number of observations-1. If there is only one observation, it is normalized by 1.

• C由观察数-1归一化。 如果只有一个观察值，则将其标准化为1。

• If A is a scalar, cov(A) returns 0. If A is an empty array, cov(A)returns NaN.

• 如果A是标量，则cov（A）返回0.如果A是空数组，则cov（A）返回NaN。

（你看看人家考虑的多周全！）

---

C = cov(A,B) 

C = cov(A,B) returns the covariance between two random variables A and B.

C = cov(A,B) 返回两个随机变量A和B之间协方差。

• If A and B are vectors of observations with equal length, cov(A,B) is the 2-by-2 covariance matrix.

• 如果A和B是同等长度的观测向量，那么C是一个2*2的协方差矩阵。

• If A and B are matrices of observations, cov(A,B) treats A and B as vectors and is equivalent to cov(A(:),B(:)). A and B must have equal size.

• 如果A和B是观察矩阵，则cov（A，B）将A和B视为向量，并且等同于cov（A（:)，B（:)）。 A和B必须具有相同的大小。

• If A and B are scalars, cov(A,B) returns a 2-by-2 block of zeros. If A and B are empty arrays, cov(A,B) returns a 2-by-2 block of NaN.

• 如果A和B是标量，则cov（A，B）返回2乘2的零块。 如果A和B是空数组，则cov（A，B）返回2乘2的NaN块。

---

C = cov(___,w)

C = cov(___,w) specifies the normalization weight for any of the previous syntaxes. When w = 0 (default), C is normalized by the number of observations-1. When w = 1, it is normalized by the number of observations.

C = cov（___，w）指定任何先前语法的归一化权重。 当w = 0（默认值）时，C由观测数-1归一化。 当w = 1时，它通过观察次数归一化。

---

C = cov(___,nanflag)

C = cov(___,nanflag) specifies a condition for omitting NaN values from the calculation for any of the previous syntaxes. For example, cov(A,'omitrows') will omit any rows of A with one or more NaN elements.

C = cov（___，nanflag）指定从任何先前语法的计算中省略NaN值的条件。 例如，cov（A，'omitrows'）将省略具有一个或多个NaN元素的A的任何行。

---

示例

下面举例说明重要的语法格式：

C = cov(A) 举例（矩阵的协方差）

Create a 3-by-4 matrix and compute its covariance

A = [5 0 3 7; 1 -5 7 3; 4 9 8 10];
C = cov(A)

C = 4×4

    4.3333    8.8333   -3.0000    5.6667
    8.8333   50.3333    6.5000   24.1667
   -3.0000    6.5000    7.0000    1.0000
    5.6667   24.1667    1.0000   12.3333

Since the number of columns of A is 4, the result is a 4-by-4 matrix.

由于矩阵A有4列，表示有4个随机变量，那么协方差矩阵是4*4的。

---

cov(A,B) 举例之两个向量之间的协方差

1. Create two vectors and compute their 2-by-2 covariance matrix.

A = [3 6 4];
B = [7 12 -9];
cov(A,B)

ans = 2×2

    2.3333    6.8333
    6.8333  120.3333

cov(A,B) 举例之两个矩阵之间的协方差

2. Create two matrices of the same size and compute their 2-by-2 covariance.

A = [2 0 -9; 3 4 1];
B = [5 2 6; -4 4 9];
cov(A,B)

ans = 2×2

   22.1667   -6.9333
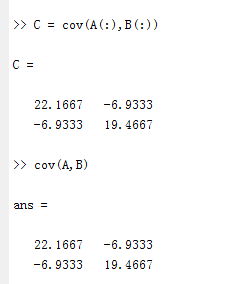
   -6.9333   19.4667

这相当于求A(:)和B(:)的协方差，如下验证下：

对比下cov(A,B)发现是一致的：

Specify Normalization Weight

创建一个矩阵并计算由行数归一化的协方差。

A = [1 3 -7; 3 9 2; -5 4 6];
C = cov(A,1)

C = 3×3

   11.5556    5.1111  -10.2222
    5.1111    6.8889    5.2222
  -10.2222    5.2222   29.5556

我觉得还是有必要比较下不归一化的情况：

>> A = [1 3 -7; 3 9 2; -5 4 6]

A =

     1     3    -7
     3     9     2
    -5     4     6

>> C = cov(A,1)

C =

   11.5556    5.1111  -10.2222
    5.1111    6.8889    5.2222
  -10.2222    5.2222   29.5556

>> C = cov(A)

C =

   17.3333    7.6667  -15.3333
    7.6667   10.3333    7.8333
  -15.3333    7.8333   44.3333

Covariance Excluding NaN

创建矩阵并计算其协方差，排除包含NaN值的任何行。

A = [1.77 -0.005 3.98; NaN -2.95 NaN; 2.54 0.19 1.01]

A = 3×3

    1.7700   -0.0050    3.9800
       NaN   -2.9500       NaN
    2.5400    0.1900    1.0100

C = cov(A,'omitrows')

C = 3×3

    0.2964    0.0751   -1.1435
    0.0751    0.0190   -0.2896
   -1.1435   -0.2896    4.4104