A*搜索算法(Java实现)
引言
1968年,的一篇论文,“P. E. Hart, N. J. Nilsson, and B. Raphael. A formal basis for the heuristic determination of minimum cost paths in graphs. IEEE Trans. Syst. Sci. and Cybernetics, SSC-4(2):100-107, 1968”。从此,一种精巧、高效的算法------A*算法横空出世了,并在相关领域得到了广泛的应用。
A* 搜索算法
图形搜索算法,从给定起点到给定终点计算出路径。其中使用了一种启发式的估算,为每个节点估算通过该节点的最佳路径,并以之为各个地点排定次序。算法以得到的次序访问这些节点。因此,A*搜索算法是最佳优先搜索的范例。
Graph search algorithm that finds a path from a given initial node to a givengoal node. It employs a heuristic estimate that ranks each node by an estimateof the best route that goes through that node. It visits the nodes in order ofthis heuristic estimate. The A* algorithm is therefore an example of best-firstsearch.
相关概念
搜索区域(The Search Area)
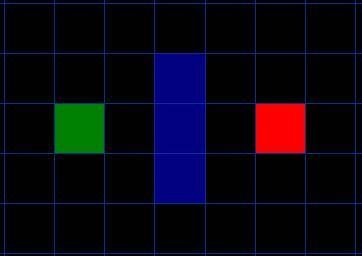
我们假设某人要从 A 点移动到 B 点,但是这两点之间被一堵墙隔开。如图 1 ,绿色是 A ,红色是 B ,中间蓝色是墙。
搜索区域划分为一个矩阵
通过图片我们可以发现,我们把要搜寻的区域划分成了正方形的格子,一个矩阵。这是寻路的第一步,简化搜索区域,就像我们这里做的一样。这个特殊的方法把我们的搜索区域简化为了 2 维数组。数组的每一项代表一个格子,它的状态就是可走 (walkalbe) 和不可走 (unwalkable) 。通过计算出从 A 到 B需要走过哪些方格,就找到了路径。一旦路径找到了,人物便从一个方格的中心移动到另一个方格的中心,直至到达目的地。
方格的中心点我们成为“节点 (nodes) ”。如果你读过其他关于 A* 寻路算法的文章,你会发现人们常常都在讨论节点。为什么不直接描述为方格呢?因为我们有可能把搜索区域划为为其他多变形而不是正方形,例如可以是六边形,矩形,甚至可以是任意多变形。而节点可以放在任意多边形里面,可以放在多变形的中心,也可以放在多边形的边上。我们使用这个系统,因为它最简单。
开始搜索(Starting the Search)
一旦我们把搜寻区域简化为一组可以量化的节点后,就像上面做的一样,我们下一步要做的便是查找最短路径。在 A* 中,我们从起点开始,检查其相邻的方格,然后向四周扩展,直至找到目标。
我们这样开始我们的寻路旅途:
1. 从起点 A 开始,并把它就加入到一个由方格组成的 open list( 开放列表 ) 中。这个 open list 有点像是一个购物单。当然现在 open list 里只有一项,它就是起点 A ,后面会慢慢加入更多的项。 Open list 里的格子是路径可能会是沿途经过的,也有可能不经过。基本上 open list 是一个待检查的方格列表。
2.查看与起点 A 相邻的方格 ( 忽略其中墙壁所占领的方格,河流所占领的方格及其他非法地形占领的方格 ) ,把其中可走的 (walkable) 或可到达的 (reachable) 方格也加入到 open list 中。把起点 A 设置为这些方格的父亲 (parent node 或 parent square) 。当我们在追踪路径时,这些父节点的内容是很重要的。稍后解释
3. 把 A 从 open list 中移除,加入到 close list( 封闭列表 ) 中, close list 中的每个方格都是现在不需要再关注的。如下图所示,深绿色的方格为起点,它的外框是亮蓝色,表示该方格被加入到了 close list 。与它相邻的黑色方格是需要被检查的,他们的外框是亮绿色。每个黑方格都有一个灰色的指针指向他们的父节点,这里是起点 A 。
每个邻接点都有一个指向当前点的指针
下一步,我们需要从 open list 中选一个与起点 A 相邻的方格,按下面描述的一样或多或少的重复前面的步骤。但是到底选择哪个方格好呢?具有最小 F 值的那个。
路径排序(Path Sorting)计算出组成路径的方格的关键是下面这个等式:
F = G + H
这里,G = 从起点 A 移动到指定方格的移动代价,沿着到达该方格而生成的路径。
H = 从指定的方格移动到终点 B 的估算成本。在接下来的代码中,我计算H采用的是Monhattan距离,这个距离是指忽略图中的障碍物,仅考虑横向和纵向的移动,在用而二维数组表示的方式中:
H=Math.abs(end.X-current.X)+Math.abs(end.Y-current.Y),为了和下述的G值保持相同的权重,我们将H扩大了10倍,即H=H*10。
G 是从起点A移动到指定方格的移动代价。在本例中,横向和纵向的移动代价为 10 ,对角线的移动代价为 14 。为什么是14二不是13或15呢?根据勾股定理我们可以知道:sqrt(10*10+10*10)约等于14.14,取整数就为14了。
关于 Manhattan 方法,这很像统计从一个地点到另一个地点所穿过的街区数,而你不能斜向穿过街区。重要的是,计算 H 是,要忽略路径中的障碍物。这是对剩余距离的估算值,而不是实际值,因此才称为试探法。 把 G 和 H 相加便得到 F ,F的存在使得搜索算法有了倾向性,我们对移动代价有了一个常数的表示,这对我们算法的实现是很重要的。
我们第一步的结果如下图所示:
第一步后的结果
每个方格都标上了 F , G , H 的值,就像起点右边的方格那样,左上角是 F ,左下角是 G ,右下角是 H 。对于这张图中的数据我们做了一些处理,图中被绿色填充的那个格子我们用correntNode表示为当前所在位置,围绕corrntNode的那八个格子,我们放入一个叫做公开列表openlist的链表中,下一次我们移动的点就是openlist中F值最小的那个节点,每次移动到下一个节点之前,我们把当前节点存放到封闭列表closelist中,同时我们在openlist中把下一节点移除,这样节点就有:openlist(min)->corrent->closelist的移动流程,需要注意的,这个过程是移动的,不能进行复制。
现在我们把所有步骤放在一起:
1. 把起点加入 open list 。
2. 重复如下a,b,c,d四个步骤:
a. 遍历 open list ,查找 F 值最小的节点,把它作为当前要处理的节点。
b.把这个节点移到 close list 。
c.对当前方格的 8 个相邻方格的每一个方格?
◆ 如果它是不可抵达的或者它在 close list 中,忽略它。否则,做如下操作。
◆ 如果它不在 open list 中,把它加入 open list ,并且把当前方格设置为它的父亲,记录该方格的 F , G 和 H 值。
◆ 如果它已经在 open list 中,检查这条路径 ( 即经由当前方格到达它那里 ) 是否更好,用 G 值作参考。更小的 G 值表示这是更好的路径。如果是这样,把它的父亲设置为当前方格,并重新计算它的 G 和 F 值。如果你的 open list 是按 F 值排序的话,改变后你可能需要重新排序。
d. 停止条件:
◆ 把终点加入到了 open list 中,此时路径已经找到了;
或者◆ 查找终点失败,并且 open list 是空的,此时没有路径。
3. 保存路径。从终点开始,每个方格沿着父节点移动直至起点,这就是你的路径。
下面是本人的对A*搜索树的java实现代码:
数据结构类Node.java
package thirty_two.A_Search;
/**
* 节点链表类
* @author
*
*/
public class Node {
public int X;
public int Y;
public int F;
public int H;
public int G;
public Node parent;
public boolean canSearch=false; //用于判断F H G值是否给定
public void updateFG(int g) {
G=g;
F=G+H;
}
public Node(int x, int y, int f, int h, int g, Node parent) {
super();
X = x;
Y = y;
F = f;
H = h;
G = g;
this.parent = parent;
canSearch=true;
}
public Node() {
super();
}
public Node(int x, int y, int h, int g, Node parent) {
super();
X = x;
Y = y;
H = h;
G = g;
F=g+h;
this.parent = parent;
canSearch=true;
}
@Override
public String toString() {
return "Node [X=" + X + ", Y=" + Y + ", F=" + F + ", H=" + H + ", G=" + G + ", parent=" + parent
+ ", canSearch=" + canSearch + "]";
}
}
算法计算类ASearch.java:
package thirty_two.A_Search;
/**
* A*搜索算法
* @author
* 规定数字大于5的表示为障碍物
* 数字为1表示起点 数字2表示终点
* 小于0的数用作标记处理
*/
import java.util.ArrayList;
import java.util.LinkedList;
public class ASearch {
public LinkedList closelist=new LinkedList();
public LinkedList openlist=new LinkedList();
private Node start;
private Node end;
// public ASearch() { //不允许无参构造
// super();
// }
public ASearch(Node start, Node end) {
super();
this.start = start;
this.end = end;
}
public Node getStart() {
return start;
}
public void setStart(Node start) {
this.start = start;
}
public Node getEnd() {
return end;
}
public void setEnd(Node end) {
this.end = end;
}
//检查start end 若G H F值不存在则初始化
public void checkGHF() {
if(!start.canSearch||!end.canSearch) {
start.G=0;
start.H=Math.abs(end.X-start.X)+Math.abs(end.Y-start.Y);
start.F=start.G+start.H;
end.G=0;
end.H=0;
end.F=0;
}
}
public Node findPath(int[][] map){ //搜索区域划分为二维数组
checkGHF();
Node correntNode=null; //当前节点
//1.将start加入openlist
openlist.add(start);
map[start.X][start.Y]=-1; //标记为已加入openlist
//退出条件 openlist为空 或者 openlist将终点包含进来
while (!openlist.isEmpty()) {
//获得openlist中F最小的节点 并设为当前节点
correntNode=openlist.getFirst();
System.out.println(correntNode.toString());
//将当前节点加入closelist
closelist.add(correntNode);
openlist.remove(correntNode);
map[correntNode.X][correntNode.Y]=-2; //标记为已加入closelist
//更新openlist
if(updateOpenlist(correntNode,map)) {
break;
};
System.out.println(openlist.size());
}
return correntNode;
}
//根据F值插入链表 维护链表
public void insert(Node node) {
if(openlist.size()==0) {
openlist.addFirst(node);
return;
}
int i=0;
while (node.F>openlist.get(i).F) {
i++;
if(i>=openlist.size()) {
openlist.addLast(node);
return ;
}
}
openlist.add(i, node);
}
//更新openlist
public boolean updateOpenlist(Node node,int[][] map) {
// openlist.clear();
//更新当前节点的openlist与原来openlist交集中数据的FG值
ArrayList indexList=new ArrayList();
for(int i=0;i=1&&node.X=1&&node.Y4) {
continue;
}
//对点不可达情况
if(i!=x&&j!=y&&(map[i][y]>4||map[x][j]>4)) {
continue;
}
//当前点不存在openlist中
if(map[i][j]!=-1) {
int g=0;
if(i!=x&&j!=y) {
g=14;
}else {
g=10;
}
Node newnode=new Node(i, j, getH(i,j), g, node);
insert(newnode);
}
}
}
}
/**
* 接下来我们就要考虑如果当前点处于边界的情况了
* 在处于边界的时候,我们就检查的零接点个数就变得不确定了
*/
return false;
}
/*
* 重排openlist维持有序 基于此特殊情况的排序方式
* 排序原则:先将变动的node复制一份,在openlist去除变动过得node
* 在根据大小重新插入
*/
public void sortOpenlist(ArrayList list) {
LinkedList temp=new LinkedList();
for (int i=list.size()-1;i>=0;i--) {
temp.add(openlist.get(list.get(i)));
openlist.remove(list.get(i));
}
openlist.clear(); //将不包含在新节点的零接节点范围的点清除
for(int i=0;i 文章借鉴于:https://www.gamedev.net/articles/programming/artificial-intelligence/a-pathfinding-for-beginners-r2003/