noip数据结构与算法 之 基础小算法 二维前缀和维护
noip数据结构与算法 之 基础小算法 二维前缀和维护
相信来看二维前缀和维护的各位一定是对一维前缀和维护问题有足够的了解了,那么二维的前缀和维护实际上是在一维前缀和维护的基础上的升级,把一个数列升级成了矩阵,但是思想是一样的,具体问题如下:
问题描述:
已知n*n的矩阵a,有m次询问,每次询问给定 x 1 , y 1 , x 2 , y 2 x_1,y_1,x_2,y_2 x1,y1,x2,y2四个数,求以 ( x 1 , y 1 ) (x_1,y_1) (x1,y1)为左上角坐标和 ( x 2 , y 2 ) (x_2,y_2) (x2,y2)为右下角坐标的子矩阵的所有元素和。注意仍然包含左上角和右下角的元素。
输入数据:
第一行n和m,接下来一行有n行,每行n个数,表示矩阵a,接下来有m行,每行有四个数 x 1 , y 1 , x 2 , y 2 x_1,y_1,x_2,y_2 x1,y1,x2,y2,详细解释参考问题描述。
输出数据:
m行,每行一个求和解。
输入样例:
5 2
1 2 3 4 5
6 7 8 9 10
11 12 13 14 15
16 17 18 19 20
21 22 23 24 25
2 2 4 4
3 3 5 5
输出样例:
117
171
数据范围:
0 < N ≤ 1000 ; 0 < M ≤ 100000 0 \lt N \le 1000;0 \lt M \le 100000 0<N≤1000;0<M≤100000
a i , j a_{i,j} ai,j是int范围内的任意整数
我们肯定能够想到,如果单纯的使用暴力解决这个问题是 O ( m n 2 ) O(mn^2) O(mn2)的做法,对于这个题的数据范围是绝对超时的。所以我们也能想到是使用了一个类似于一维前缀和维护的优化方法的优化方式。但那是什么?当我们转换成为矩阵的时候,前n项和的做法就不行了。
但我们还有一个东西叫做容斥定理。容斥定理是关于集合的一个定理。这个定理是小学奥数内容,而且我们在高中课程中学习集合的时候已经了解过了,但你或许不知道这个名字。
在小学奥数中,容斥定理被描述的极其简单,如果我有n个抽屉,有m个苹果,我往抽屉里面放苹果,保证每个抽屉都有苹果的情况下,如果 k n < m kn \lt m kn<m,那么必定会有一个抽屉有至少k+1个苹果。
当然,在我们学习过集合之后,容斥定理就可以这样来描述:
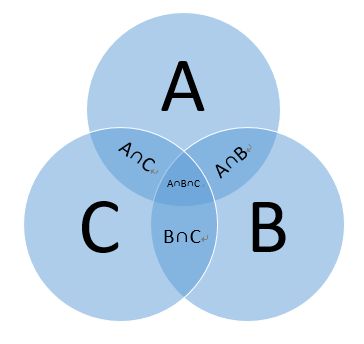
设有A,B,C三个集合,这三个集合相互均有交集,并且三个集合之间也有交集。则这三个集合的并集可以表示为:
A ∪ B ∪ C = A + B + C − A ∩ B − B ∩ C − A ∩ C + A ∩ B ∩ C A \cup B \cup C=A+B+C-A \cap B-B \cap C-A \cap C+A \cap B \cap C A∪B∪C=A+B+C−A∩B−B∩C−A∩C+A∩B∩C
我们使用文氏图可以得到一个更直观的解释:
相信数学好的同学已经通过图看出来这个公式了,用更通俗易懂的道理来解释,三个集合,首先直接相加,发现 A ∩ B A \cap B A∩B和 B ∩ C B \cap C B∩C和 A ∩ C A \cap C A∩C的三个部分被重复添加了,之后减去这三个部分,又发现 A ∩ B ∩ C A \cap B \cap C A∩B∩C的部分都被减去了三次,实际上对于这部分被加了三次(在A+B+C的时候这部分就被加了三次)之后又减了三次(在减去 A ∩ B A \cap B A∩B和 B ∩ C B \cap C B∩C和 A ∩ C A \cap C A∩C的时候分别被减去了一次),实际上就跟没加过没减过一样,所以我们要再加一次。所以公式就变成上面那个样子。
这里我们只推了3个集合的容斥定理,对于多个集合思路是一样的。我们可以把所有集合相加,同时减去所有偶数重复,加上所有奇数重复。简单来记忆就是减偶加奇。这个过程可以自己推导,所以这里不再赘述。
现在我们来把这个定理应用到我们的矩阵上。现在我们用 S ( x 1 , y 1 , x 2 , y 2 ) S(x_1,y_1,x_2,y_2) S(x1,y1,x2,y2)表示以 ( x 1 , y 1 ) (x_1,y_1) (x1,y1)为左上元素和以 ( x 2 , y 2 ) (x_2,y_2) (x2,y2)为右下元素的矩阵中所有元素的和。对于任意 S ( x 1 , y 1 , x 2 , y 2 ) S(x_1,y_1,x_2,y_2) S(x1,y1,x2,y2),它一定等于 S ( 1 , 1 , x 2 , y 2 ) S(1,1,x_2,y_2) S(1,1,x2,y2)加上 S ( 1 , 1 , x 1 − 1 , y 1 − 1 ) S(1,1,x_1-1,y_1-1) S(1,1,x1−1,y1−1)减去 S ( 1 , 1 , x 1 − 1 , y 2 ) S(1,1,x_1-1,y_2) S(1,1,x1−1,y2)减去 S ( 1 , 1 , x 2 , y 1 − 1 ) S(1,1,x_2,y_1-1) S(1,1,x2,y1−1)。也就是这个公式:
S ( x 1 , y 1 , x 2 , y 2 ) = S ( 1 , 1 , x 2 , y 2 ) + S ( 1 , 1 , x 1 − 1 , y 1 − 1 ) − S ( 1 , 1 , x 1 − 1 , y 2 ) − S ( 1 , 1 , x 2 , y 1 − 1 ) S(x_1,y_1,x_2,y_2)= S(1,1,x_2,y_2)+S(1,1,x_1-1,y_1-1)- S(1,1,x_1-1,y_2)-S(1,1,x_2,y_1-1) S(x1,y1,x2,y2)=S(1,1,x2,y2)+S(1,1,x1−1,y1−1)−S(1,1,x1−1,y2)−S(1,1,x2,y1−1)
下面我们举个例子来解释下这个公式:
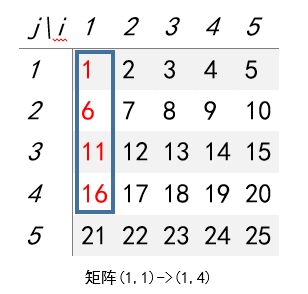
以这个矩阵为例,i,j是这个矩阵的两个下标,我们计算S(2,2,4,4):
按照公式我们首先计算 S ( 1 , 1 , x 2 , y 2 ) S(1,1,x_2,y_2) S(1,1,x2,y2),也就是S(1,1,4,4),这个矩阵是以(1,1)为左上角,以(4,4)为右下角,它的和是(1+2+3+4+6+7+8+9+11+12+13+14+16+17+18+19)。
之后我们调换一下顺序,计算一下 − S ( 1 , 1 , x 1 − 1 , y 2 ) -S(1,1,x_1-1,y_2) −S(1,1,x1−1,y2),也就是-S(1,1,1,4)这个矩阵,表示以(1,1)为左上角,以(1,4)为右下角的矩阵,减去这部分的和,即-(1+6+11+16)。
之后再计算 − S ( 1 , 1 , x 2 , y 1 − 1 ) - S(1,1,x_2,y_1-1) −S(1,1,x2,y1−1),也就是-S(1,1,4,1)这个矩阵,表示以(1,1)为左上角,(4,1)为右下角的矩阵,减去这部分的和,就是-(1+2+3+4)。
根据之前讲的容斥定理不难发现,以(1,1)为左上角且以 ( x 1 − 1 , y 1 − 1 ) (x_1-1,y_1-1) (x1−1,y1−1)为右下角的矩阵(在这里就是(1,1)位置的元素)被加和了一次减去了两次,所以我们要再加一次,所以加1。
最终我们做了(1+2+3+4+6+7+8+9+11+12+13+14+16+17+18+19)-(1+6+11+16)-(1+2+3+4)+1,恰好是(2,2)为左上角(4,4)为右下角的矩阵和(即7+8+9+12+13+14+17+18+19)。下面我用一个图来解释刚才的四处矩阵。
从图不难看出,我们首先加上蓝色矩阵,然后减去黄色矩阵,减去红色矩阵,发现棕色矩阵被减去了两次而加了一次,根据容斥定理,我们应该再加一次棕色矩阵,最后结果就是我们蓝色的9个数字的和,这就是我们要求得的子矩阵了。结合上面的解释,最后就是这个公式:
S ( x 1 , y 1 , x 2 , y 2 ) = S ( 1 , 1 , x 2 , y 2 ) + S ( 1 , 1 , x 1 − 1 , y 1 − 1 ) − S ( 1 , 1 , x 1 − 1 , y 2 ) − S ( 1 , 1 , x 2 , y 1 − 1 ) S(x1,y1,x_2,y_2)= S(1,1,x_2,y_2)+S(1,1,x_1-1,y_1-1)- S(1,1,x_1-1,y_2)-S(1,1,x_2,y_1-1) S(x1,y1,x2,y2)=S(1,1,x2,y2)+S(1,1,x1−1,y1−1)−S(1,1,x1−1,y2)−S(1,1,x2,y1−1)
所以接下来我们发现,对于任何一个矩阵的求和,我都只需要知道以(1,1)为左上角的四个矩阵的和就行了,这个问题只需要一个 O ( n 2 ) O(n^2) O(n2)的算法就能解决。这个算法类似于刚刚求子矩阵的和的算法,我们要新算出一个数组 S i , j S_{i,j} Si,j,对于这个数组中的某一元素 S i , j S_{i,j} Si,j表示以(1,1)为左上角,(i,j)为右下角的矩阵的元素和。
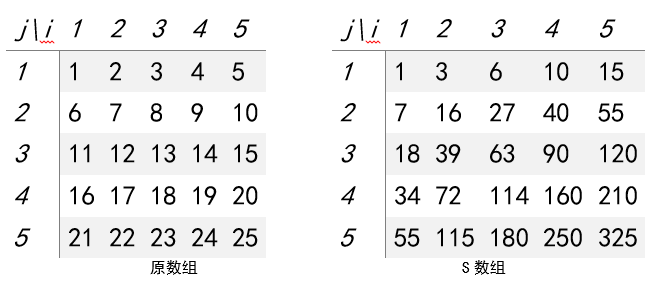
以刚刚的数组为例:
观察这里的S数组,我们不难发现,对于第一行来说,都可以按照一维的处理方法处理,对于第一列来说也是如此的处理,那么对于其他位置的数呢?我们假设原来的数组是 a i , j a_{i,j} ai,j则满足 S i , j = a i , j + S i − 1 , j + S i , j − 1 − S i − 1 , j − 1 S_{i,j}=a_{i,j}+S_{i-1,j}+S_{i,j-1}-S_{i-1,j-1} Si,j=ai,j+Si−1,j+Si,j−1−Si−1,j−1,这个可以用刚刚的容斥定理来解释,对于4格的矩阵而言,这里以(2,2)为左上角(3,3)为右下角的矩阵举例,计算S3,3的公式就是 S 3 , 3 = a 3 , 3 + S 2 , 3 + S 3 , 2 − S 2 , 2 S_{3,3}=a_{3,3}+S_{2,3}+S_{3,2}-S_{2,2} S3,3=a3,3+S2,3+S3,2−S2,2,可以看着上面的两个数组表来对应一下, a 3 , 3 a_{3,3} a3,3就是13, S 2 , 3 S_{2,3} S2,3是39, S 3 , 2 S_{3,2} S3,2是27, S 2 , 2 S_{2,2} S2,2是16,最后结果就是63。并且我们不难发现,我们计算 S i , j S_{i,j} Si,j的值只需要 S i − 1 , j , S i , j − 1 S_{i-1,j},S_{i,j-1} Si−1,j,Si,j−1和 S i − 1 , j − 1 S_{i-1,j-1} Si−1,j−1这三个数,而这三个数按照自上而下自左而右的遍历顺序已经被计算出来了,而最上一行和最左一列都可以单独处理,于是我们的S数组就求出来了,接下来根据之前的公式就可以算出任意的子矩阵的求和了。这样的算法时间复杂度就是 O ( m + n 2 ) O(m+n^2) O(m+n2)。
以上就是对二维前缀和问题的介绍。
我的代码如下:
#include
#include
#include
#include
#include
#include
#include
using namespace std;
const int MAXN=1010;
int n,m,a[MAXN][MAXN];
//读入优化
int read(){
char ch=getchar();
bool fl=0;
int r=0;
if(ch=='-'){
fl=1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
r*=10;
r+=ch-'0';
ch=getchar();
}
return fl?-r:r;
}
//输出优化
void write(int x){
if(x<0){
putchar('-');
x=-x;
}
if(x>9){
write(x/10);
}
putchar(x%10+'0');
}
int main(){
freopen("in.txt","r",stdin);
freopen("std.txt","w",stdout);
n=read();
m=read();
//前n项子矩阵和求法,O(n*n)复杂度
a[0][0]=read();
for(int i=1;i