SOLO: Segmenting Objects by Locations 论文学习

Abstract

本文提出了一个新的、简洁的图像实例分割方法。与密集预测的任务相比（如语义分割），实例的个数是任意的，这使得实例分割非常有挑战性。为了对每个实例都预测一个 mask，主流的方法要么延续了“先检测后分割”的策略（如 Mask R-CNN），要么采用聚类的方法将像素点聚合为各个实例。本文则从一个全新的角度来看待实例分割问题，提出了“实例类别”的概念，根据实例的位置和大小，对每个实例的像素点赋予一个类别，巧妙地将实例掩码分割问题转换为一个分类问题。这样，实例分割就被分解成了两个分类任务。本文证明了该方法更加简单、灵活，性能也更好，它可以取得与 Mask RCNN 相似的准确率，超越其它的单阶段实例分割算法。

1. Introduction

实例分割非常有挑战性，因为它需要将图像中所有的物体都准确地区分出来，同时在语义层面的像素点级别上，分割出每个实例。图像中的物体都属于一个大小固定的语义类别集合，但是实例的个数是变化的。这样，语义分割就很容易地表示为一个密集的、逐像素点的分类问题，然而直接用这个模式对实例的标签进行预测是很有难度的。

为了克服这个问题，近来的实例分割方法可以分为两类，即自上而下的和自下而上的模式。前者即“先检测再分割”的方法，首先检测边框，然后在每个边框内分割实例的掩码。后者学习一个关联程度，对每个像素点都赋予一个 embedding 向量，将不同实例的像素点拉开，相同实例的像素点拉近。然后使用聚合后处理方法，将实例区分开来。这两个模式都是阶梯式的、间接的，要么依赖于准确的边框检测，要么依赖于逐像素点的 embedding 学习和聚合处理。

而本文的方法直接去分割实例的掩码，监督的主体为实例掩码标签，而非边框中的掩码或像素对之间的关系。本文的出发点为：图像中物体实例的本质差异是什么？以 MS COCO 数据集为例，它的验证集中总共有36780个物体，$98.3\%$的物体对之间的中心距离超过30个像素点。剩下的$1.7\%$物体对中，$40.5\%$的大小比例超过 $1.5\times$。这里，我们不考虑极端案例，比如两个物体呈$\times$ 状。总而言之，图像中的任意两个物体，要么它们的中心位置不同，要么其物体大小不同。这个发现就让我们去猜测，是否可以通过中心位置和物体的大小来直接区分实例。

在相近的领域（语义分割）中，现在主导的方法就是利用一个全卷积网络，输出$N$个通道的密集预测。每个输出通道负责一个语义类别（包括背景类）。语义分割旨在区分不同的语义类别。相似地，为了区分图像中的物体实例，本文提出了“实例类别”的概念，即量化的中心位置和物体大小，使我们通过位置信息就可以分割物体，因此该方法命名为 SOLO。

SOLO 的核心想法就是通过位置和大小信息来区分物体实例。

位置 一张图片可以分割为$S\times S$ 个网格，这样就有了$S^2$个中心位置类别。根据物体中心的坐标，将物体实例指派给一个网格，作为其中心位置类别。与 DeepMask 和 TensorMask 不同，它们将掩码放置在通道维度上，本文将中心位置类别编码为通道维度，这和语义分割中的语义类别相似。每个输出通道负责一个中心位置类别，相应的通道图预测该类别的物体实例掩码。因此，结构几何信息自然地就保留在了空间矩阵中。

本质上，实例类别近似一个实例的中心位置。因此，对每个像素点进行实例类别的分类，与对每个像素点进行回归来预测物体的中心位置是等价的。将位置预测任务转化为分类问题，而不是回归问题的意义在于，分类通过固定个数的通道对不同数量的实例进行建模更加直接而且简单，而且不依赖于后处理方法（如聚合操作或 embedding 学习）。

大小 为了区分不同大小的实例，本文使用了特征金字塔网络（FPN），将不同大小的物体分配到不同的特征图层级，作为物体大小类别。这样所有的实例都区分对待，使我们可以通过“实例类别”来对物体进行分类。注意，FPN 的目的在于检测图像中不同大小的物体。

作者证明了FPN对本文方法是至关重要的，对于分割的表现有很明显的作用，尤其是变动大小的物体。

有了SOLO框架，仅通过掩码标签，我们就可以对端到端的实例分割进行优化，突破传统的局部边框检测和像素点聚合方法，直接进行像素级别的实例分割。注意，大多数的实例分割方法都需要边框标签，来作为一个监督信号。本文第一次展现了一个非常简洁的实例分割方法，在 COCO 数据集上的表现与“先检测再分割”的 Mask R-CNN 差不多。此外，在实例轮廓检测任务上，作者也展示了本方法的通用性，它将实例边界轮廓看作为一个 one-hot 二元掩码，无需任何修改，SOLO 能够产生非常理想的实例轮廓。SOLO 只需解决2个像素级别的分类任务，这与语义分割类似。因此，我们可以借鉴最近语义分割领域的一些进展，提升SOLO方法。通过离散量化，SOLO 将坐标回归问题转化为分类问题。这样做的一个好处就是避免了 YOLO 中用到的坐标归一化操作和log变换。SOLO 方法的简洁与超强表现使其能广泛应用在实例级别的识别任务上。

2. Related Work

作者回顾了一些与本文有关的实例分割方法。

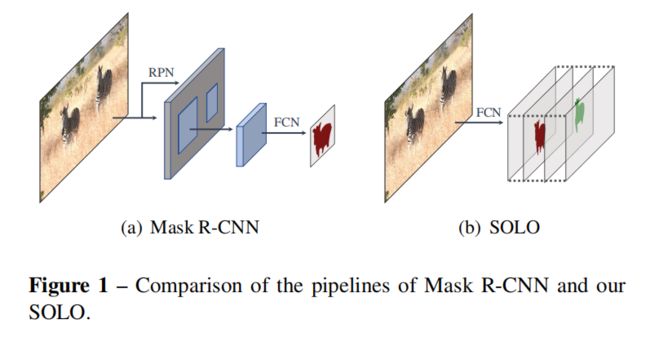
自上而下的实例分割。这些方法首先得到一个先验的边框，然后再进行实例分割。FCIS 在兴趣区域内将FPN生成的位敏得分图组合起来，预测实例掩码。Mask R-CNN 扩展了 Faster R-CNN 检测器，增加了一个分支，在检测边框内对物体实例进行分割。基于 Mask R-CNN， PANet 进一步增强了特征表示，提升其准确率。 Mask Scoring R-CNN 增加了一个 mask-IoU 分支，判断预测掩码的质量，对其进行打分，提升其表现。TensorMask 采用了密集的滑动窗方法，通过预先设定的滑动窗个数与尺度对每个像素点进行实例分割。与自上而下的方法不同，SOLO 没有采用边框，就不会受到 anchor 边框位置与尺度的限制，可以很自然地获取全卷积网络的好处。

自下而上的实例分割。这种方法将像素点聚合为任意数量的物体实例，产生实例掩码。本文简单地介绍了几个最新进展。
[19] 通过学习关联 embeddings，将像素点聚合为各个实例。[5] 提出了一个判别损失函数，高效地学习像素级别的实例 embeddings，将不同实例的像素点推开，相同实例的像素拉近。SGN[15] 将实例分割问题拆解为一序列的 sub-grouping 问题。SSAP[6] 学习一对像素的关联金字塔，即这俩像素点属于同一物体的概率，然后通过级联的图划分方法产生实例。通常自下而上的方法的精度要落后于自上而下的方法，尤其当数据集的场景和语义类别非常多样。SOLO 在训练过程中直接学习实例掩码的标签，端到端地预测实例的掩码与语义类别，无需后处理流程。

直接实例分割。据我们所知，至今没有哪种方法只通过掩码标签来训练，而无需任何的后处理操作，一次性地预测实例掩码和语义类别。近来的一些方法可以看作为“半直接”的方式。AdaptIS[24] 首先预测一些候选点，然后依次生成候选点上的物体掩码。PolarMask[27] 提出用极特征（polar representation）来编码掩码，将逐像素的掩码预测转换为距离回归问题。这俩方法都不需要边框来训练，但要么就是阶梯式的，要么进行了妥协（掩码的参数表示比较粗糙）。SOLO 用一张图片作为输入，以全卷积的形式直接输出实例掩码以及相应的类别概率，无需边框和聚合操作。该方法非常简单，可以端到端地优化，无需边框来监督其训练。预测时，对于每个实例，网络直接将输入图片映射为掩码，而无需中间的操作符如 RoI 特征裁剪或聚合后处理等。

3. SOLO

3.1 Problem Formulation

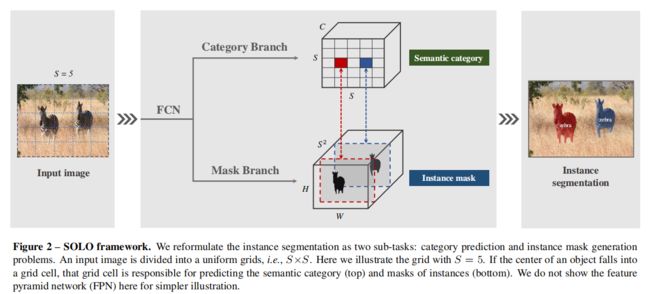
给定一张图片，实例分割方法需要判断它里面是否存在语义物体的实例；如果有，该方法需要返回分割掩码。SOLO 的核心思想就是将实例分割问题重新表示为两个同时发生的子问题：类别预测和实例掩码生成。具体点就是，该方法将输入图像划分为若干一致的网格，即$S\times S$。如果物体的中心落在某网格内，该网格就要负责：1）预测语义类别，2）分割该物体实例。

3.1.1 语义类别

对于每个网格，SOLO 预测一个$C$维度的输出，表示语义类别的概率，$C$是类别的个数。这些概率值取决于这些网格。如果我们将图像划分为$S\times S$ 个网格，则输出空间为$S\times S\times C$，如图2（上）所示。这样设计是基于一个假定，即每一个网格都属于一个单独的实例，因此只属于一个语义类别。在推理时，$C$维度的输出表示每个实例的类别概率。

3.1.2 实例掩码

与语义类别预测平行，每个 positive 网格都会输出一个相应的实例掩码。给定一个输入图片$I$，我们将之划分为$S\times S$ 个网格，总共就有至多$S^2$ 个预测掩码。在3D 输出张量中，我们在第三个维度（通道）中直接对这些掩码进行编码。输出的实例掩码的维度就是$H_I\times W_I\times S^2$。第$k$个通道负责在第$(i,j)$个网格中分割实例，$k=i\cdot S+j$（$i,j$都是从0开始）。这样，我们就在语义类别和掩码之间构建起了一一对应的关系（图2）。

一个直接预测实例掩码的方法就是采用全卷积网络，如语义分割中的FCN。但是，传统的卷积运算在某种程度上是空间不变的。空间不变性对某些任务非常重要，如图像分类，它能带来鲁棒性。但是相反，这里我们想要的是空间变动性，或更具体地说就是，位置敏感性，因为我们的分割掩码依赖于这些网格，必须被不同的特征通道分隔开。

本文的方法非常简单：在网络的初始阶段，我们直接将归一化后的像素坐标输入进网络，受"CoordConv" 算子启发[14]。我们构建一个和输入空间大小一样的张量，它包含归一化后的像素坐标，介于$[-1,1]$。该张量然后拼接到输入特征，传递到后面的层。将输入的坐标信息给到卷积操作，我们就给传统的FCN模型添加了空间功能。CoordConv 并不是唯一的选择，例如半-卷积算子也可以，但是 CoordConv 更简洁，很容易实现。如果原来的特征张量大小是$H\times W\times D$，现在新的张量就是$H\times W\times (D+2)$，最后两个通道为$x-y$像素坐标。

构建实例分割。在SOLO中，类别预测和掩码很自然地就与网格关联起来，即$k=i\cdot S+j$。于是对于每个网格，我们就可以直接得到其最终的实例分割结果。然后我们将所有的网格结果汇总起来，就可以得到该图像的实例分割结果。最后，我们使用NMS 来得到最终的实例分割结果，而不再需要其他的后处理操作。

3.2 网络结构

SOLO 加在一个卷积主干网络后面。作者使用了 FPN，它输出一个特征金字塔，每个层级的特征图大小不同，通道数固定（通常256维）。这些特征图作为每个预测head 的输入：语义类别和实例掩码。对于不同的层级上，head 的权重共享。在不同的金字塔中，网格数可能不同。

为了证明SOLO的通用性和有效性，作者构建了多个SOLO结构。不同之处在于：(a) 特征提取的主干结构，(b)计算实例分割结果的网络 head，( c) 训练的损失函数。大多数的实验都是基于图3中的 head 结构。为了进一步研究其泛化能力，作者也使用了其它变体。我们可以发现，实例分割 head 结构很直接、简单。

3.3 SOLO 训练

3.3.1 Label Assignment

在类别预测分支中，网络需要给出$S\times S$个网格的物体类别概率。具体点就是，只有当第$(i,j)$个网格和某 ground truth 掩码的中心区域的重叠大于某阈值时，它才被认为是正样本，否则就是负样本。给定ground truth 掩码的中心点$(c_x,c_y)$，宽度$w$，高度$h$，通过缩放乘数$ϵ:(c_x,c_y,ϵw,ϵh)$来控制中心区域大小，中心点不是边框的中心，而是质心，其中$ϵ=0.2$，每个 ground truth 掩码上平均有3个正样本。这来源于 center sampling，在 Foveabox和FCOS 都有所体现。对于每个正样本，都有一个二值的掩码，也就是在上分支中标记出正例所在的网格后，找到其所对应的下分支$S^2$的通道中的一个通道进行标注。

除了实例类别的标签，作者对每个正样本也进行了二元分割。因为每张图像有$S^2$个网格，我们也有$S^2$ 个输出掩码。对于每个正样本，我们标注对应的二元掩码。人们可能会担心，掩码的顺序会影响掩码预测分支，但是，作者证明最简单的行优先顺序就可以很好地解决。

3.3.2 损失函数

本文定义损失函数如下：

$$L=L_{cate}+\lambda L_{mask}$$

其中$L_{cate}$是传统的 Focal Loss，针对语义类别分类问题。$L_{mask}$是掩码预测的损失函数。

$$L_{mask}=\frac{1}{N_{pos}}\sum _k{1}_{\{P_{i,j}^{\ast }>0\}{d}_{mask}(m_k,m_k^{\ast })}$$

这里，索引$i=\lfloor k/S\rfloor ,j=k$ mod $S$，该网格索引的顺序为从上往下、从左往右。$N_{pos}$表示正样本的个数，$p^{\ast },m^{\ast }$分别表示类别真值和掩码真值。$1$是指标函数，如果$P_{i,j}^{\ast }>0$，则为1,否则为0.

在实现的时候，作者比较了$d_{mask}$的多个实现：二元交叉熵损失，Focal Loss 和 Dice Loss。最终作者使用了 Dice Loss，因为它在训练中比较稳定且有效。等式1中的$\lambda$设为3。 Dice Loss 定义为：

$$L_{Dice}=1-D(p,q)$$

其中$D$为 dice 系数，定义为：

$$D(p,q)=\frac{2{\sum }_{x,y}(p_{x,y}\cdot q_{x,y})}{{\sum }_{x,y}{p}_{x,y}^2+{\sum }_{x,y}{q}_{x,y}^2}$$

这里$p_{x,y}$和$q_{x,y}$分别是预测soft掩码和 ground truth 掩码在$(x,y)$位置的像素值。在实验中，作者给出了更多的有关损失函数的比较。

3.4 推理

SOLO 的推理步骤很直接。给定一张图片，我们将其传递入主干网络和FPN，获得网格$(i,j)$的类别得分$p_{i,j}$，以及对应的掩码$m_k$，其中$k=i\cdot S+j$。我们首先使用一个置信度阈值$0.1$，过滤掉低置信度的预测。然后选择得分最高的500个掩码，进行NMS操作。为了将预测的 soft 掩码转换为二元掩码，作者使用了阈值0.5,对预测掩码进行二值化。保留其中前100个实例掩码用于评价。

4. Experiments

5. Decoupled SOLO

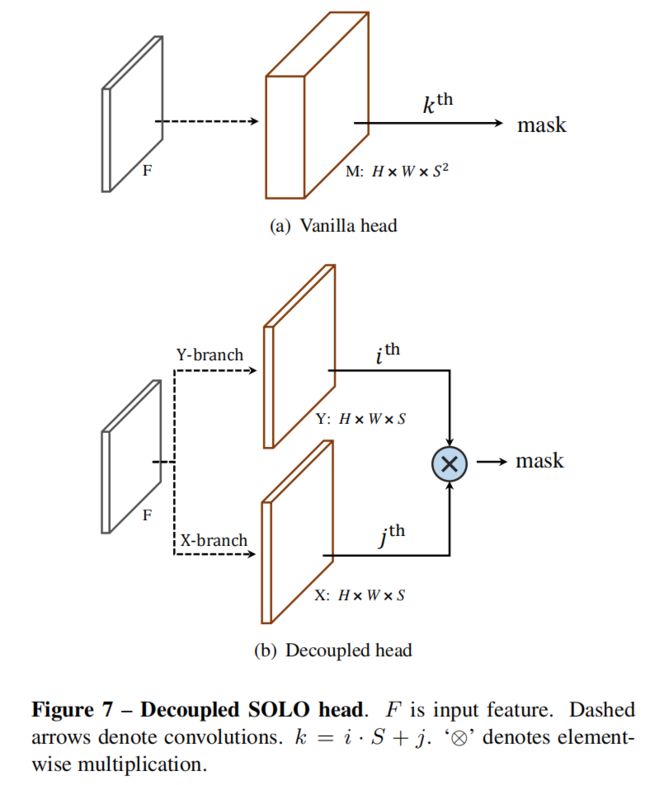
给定一个预先定义好的网格数，如 $S=20$，这样SOLO head就会输出400个通道的特征图。但是，这样预测有些冗余，因为绝大多数场景中，图像上的物体都是比较稀疏的，不太会出现特别多的物体实例。这一节，作者进一步介绍了一个等价的、更加高效率的 SOLO 模型的变体，称为 Decoupled SOLO， 如下图所示。

在Decoupled SOLO中，原始的输出张量 $M\in {\mathbb{R}}^{H\times W\times S^2}$ 被替换为两个输出张量，$X\in {\mathbb{R}}^{H\times W\times S}$ 和 $Y\in {\mathbb{R}}^{H\times W\times S}$，对应着两个坐标轴。因此，输出空间就从$H\times W\times S^2$ 降低到了$H\times W\times 2S$。对于网格位置为$(i,j)$的物体，原来的SOLO模型在输出张量$M$的第$k$个通道上分割掩码，其中$k=i\cdot S+j$。而 Decoupled SOLO 的物体掩码预测，定义为两个通道特征图的 element-wise 相乘。

$$m_k=x_j\otimes y_i$$

其中$x_j,y_i$分别表示$X$的第$j$个通道图，和$Y$的第$i$个通道图。