无向图的最小生成树

     以下内容主要参考了严蔚敏版的数据结构教材
     假设现在有n个城市，这n个城市之间最多可以修建$C_n^2=n(n-1)/2$条公路（每两个城市之间修建一条公路）。其实$n-1$条公路就可以将这n个城市全部连接起来。现在考虑的问题是如何在这$C_n^2=n(n-1)/2$条公路中选择$n-1$条公路使得修建这$n-1$条公路的话费是最小的。将城市考虑为无向图中的顶点，边考虑为两个城市之间的公路，那么边的权值则为修建该条公路的花费。这时问题就转化为求无向图的一颗生成树且该颗生成树上所有边的权值的和最小（最小生成树）。
     现在介绍求无向图的最小生成树的$Prim$算法和$Kruskal$算法：

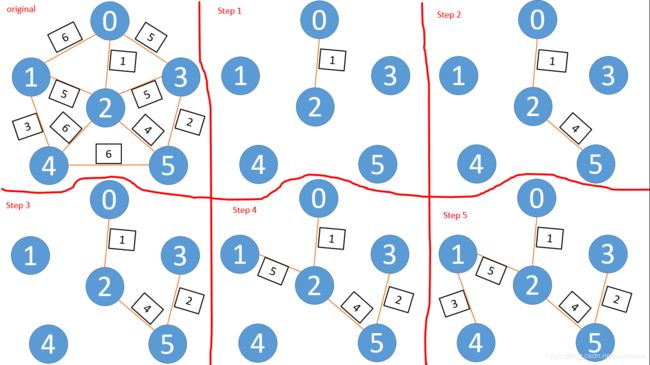
1. $Prim$算法，假设$\{V,E\}$是一个连通图，V是顶点集合E是边的集合，假设从顶点$u_0$开始构造最小生成树，初始时将顶点$u_0$加入到顶点集合U中，然后找到一条权值最小的边$\{v_x-v_y\}$并加入到边的集合TE中，其中顶点$v_x$位于集合U中，顶点$v_y$位于集合$V-U$中，这时顶点$v_x$就是顶点$u_0$，因为此时集合U中只有顶点$u_0$，现在将顶点$v_y$加入到集合U中。然后迭代以上过程直到集合U等于集合V，此时集合TE中的$n-1$条边就是所求最小生成树的边。
2. $Kruskal$算法，假设$\{V,E\}$是一个连通图，V是顶点集合E是边的集合。从状态$\{U,UE\}$开始构建最小生成树，U（初始时U=V）是顶点集合UE（初始时为空集）是边的集合。从图$\{V,E\}$中选择一条权值最小的边$\{v_x-v_y\}$加入到集合UE中，顶点$v_x$和顶点$v_y$分属于{U,UE}KaTeX parse error: Expected '}', got 'EOF' at end of input: …迭代以上过程直到{U,UE\}中所有顶点都在一个连通分量重为止，此时集合UE中的$n-1$条边就是所求最小生成树的边。

     最小生成树的MST性质：假设$\{V,E\}$是一个连通图，V是顶点集合E是边的集合，集合U是集合V的一个非空子集。如果$\{v_x-v_y\}$是一条具有最小权值的边，其中顶点$v_x$位于集合U中，顶点$v_y$位于集合$V-U$中，则必存在一颗包含边$\{v_x-v_y\}$的最小生成树。
     该性质可用反证法证明：假设连通图$\{V,E\}$的任何一颗最小生成树都不包含边$\{v_x-v_y\}$。现在假设T是连通图$\{V,E\}$的一颗最小生成树T，当将边$\{v_x-v_y\}$加入到T中时，由生成树的定义可知此时T中必然存在包含边$\{v_x-v_y\}$的回路。同时也必然存在另一条边$\{v_x^{{}^{\prime }}-v_y{}^{\prime }\}$,其中顶点$v_x^{{}^{\prime }}$位于集合U中，顶点$v_y^{{}^{\prime }}$位于集合$V-U$中，顶点$v_x$和顶点$v_x^{{}^{\prime }}$之间，顶点$v_y$和顶点$v_y^{{}^{\prime }}$之间都有通路。删去边$\{v_x^{{}^{\prime }}-v_y{}^{\prime }\}$便可消除上述回路，同时得到一颗生成树$T^{{}^{\prime }}$。又因为边$\{v_x-v_y\}$的权值小于等于边$\{v_x^{{}^{\prime }}-v_y{}^{\prime }\}$的权值，因此生成树$T^{{}^{\prime }}$上边的权值之和也小于等于最小生成树T边的权值之和。因此生成树$T^{{}^{\prime }}$是包含边$\{v_x-v_y\}$的一颗最小生成树，这与假设相矛盾，因此得证。$Prim$算法和$Kruskal$算法都是基于以上MST性质的最小生成树算法。
     图1是$Prim$算法的一个例子，$Prim$算法的测试程序也是在该例子上进行测试的。图2是$Kruskal$算法的一个例子。

　 图1.

　 图2.

#define MY_INFINITY 1000000
//图的数据结构
class MGraph
{
private:
	vector<vector<int>> adjMatrix;
	vector<int> nodeData;
	int nodeNum;

public:
	MGraph(int num)
	{
		nodeNum = num;
		nodeData = vector<int>(num, 0);
		adjMatrix = vector<vector<int>>(num, vector<int>(num));
		for (int i = 0; i < num; i++)
		{
			for (int j = 0; j < num; j++)
			{
				if (i == j)
				{
					adjMatrix[i][j] = 0;
				}
				else
				{
					adjMatrix[i][j] = MY_INFINITY;
				}
			}
		}
	}
	int getNodeNum()
	{
		return nodeNum;
	}
	void setNodeData(int data, int nodeIndex)
	{
		nodeData[nodeIndex] = data;
	}
	int getNodeData(int data, int nodeIndex)
	{
		return nodeData[nodeIndex];
	}
	void setWeight(int weight, int tail, int head)
	{
		adjMatrix[tail][head] = weight;
	}
	int getWeight(int tail, int head)
	{
		return adjMatrix[tail][head];
	}
};

class closeEdgeNode
{
private:
	int adjVex;
	int lowcost;

public:
	closeEdgeNode(int d1 = 0,int d2=0)
	{
		adjVex=d1;
		lowcost=d2;
	}
	int getAdjVex()
	{
		return adjVex;
	}
	int getLowCost()
	{
		return lowcost;
	}
	void setAdjVex(int value)
	{
		adjVex=value;
	}
	void setLowCost(int value)
	{
		lowcost=value;
	}
};

int minimumOfCloseEdge(vector<closeEdgeNode> closeEdge)
{
	int currentMinimumValue = 0;
	int currentMinimumIndex = 0;
	for (int i = 0; i < closeEdge.size(); i++)
	{
		if (closeEdge[i].getLowCost() != 0)
		{
			currentMinimumValue = closeEdge[i].getLowCost();
			currentMinimumIndex = i; 
			break;
		}
	}
	for (int j = 0; j < closeEdge.size(); j++)
	{
		if ((closeEdge[j].getLowCost() != 0)&&(closeEdge[j].getLowCost()< currentMinimumValue))
		{
			currentMinimumValue = closeEdge[j].getLowCost();
			currentMinimumIndex = j;
		}
	}
	return currentMinimumIndex;
}

void miniSpanTreePrim(MGraph g,int startNode)
{
	vector<closeEdgeNode> closeEdge(g.getNodeNum());
	for (int i = 0; i < g.getNodeNum(); i++)
	{
		if (i != startNode)
		{
			closeEdge[i].setAdjVex(startNode);
			closeEdge[i].setLowCost(g.getWeight(startNode,i));
		}
	}
	for (int i = 1; i < g.getNodeNum(); i++)
	{
		int currentMinimumIndex = minimumOfCloseEdge(closeEdge);
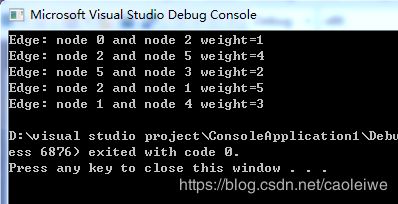
		cout << "Edge: node " << closeEdge[currentMinimumIndex].getAdjVex() << " and node " << currentMinimumIndex << " weight=" << g.getWeight(closeEdge[currentMinimumIndex].getAdjVex(), currentMinimumIndex) << endl;
		closeEdge[currentMinimumIndex].setLowCost(0);
		for (int j = 0; j < g.getNodeNum(); j++)
		{
			if (closeEdge[j].getLowCost() != 0)
			{
				if (g.getWeight(currentMinimumIndex,j)< closeEdge[j].getLowCost())
				{
					closeEdge[j].setAdjVex(currentMinimumIndex);
					closeEdge[j].setLowCost(g.getWeight(currentMinimumIndex, j));
				}
			}
		}
	}
}

//测试程序
int main()
{
	MGraph g(6);
	for (int i = 0; i < 6; i++)
	{
		g.setNodeData(i,i);
	}
	g.setWeight(1, 0, 2 );
	g.setWeight(1, 2, 0);

	g.setWeight(2, 3 ,5 );
	g.setWeight(2, 5, 3);

	g.setWeight(3, 1, 4 );
	g.setWeight(3, 4, 1);

	g.setWeight(4, 2, 5);
	g.setWeight(4, 5, 2);

	g.setWeight(5, 0, 3 );
	g.setWeight(5, 3, 0);

	g.setWeight(5, 3, 2);
	g.setWeight(5, 2, 3 );

	g.setWeight(5, 1, 2);
	g.setWeight(5, 2, 1);

	g.setWeight(6, 0, 1 );
	g.setWeight(6, 1, 0);

	g.setWeight(6, 2, 4 );
	g.setWeight(6, 4, 2);

	g.setWeight(6, 5, 4);
	g.setWeight(6, 4, 5);
	miniSpanTreePrim(g, 0);
}

　 图3.