阵列天线方向图-均匀直线/平面阵列matlab仿真

理论上发射和接收电磁波的任务可以由单个天线阵元构成的天线完成，但实际上天线要具有强方向性和高增益，要求天线波束可以扫描并具有一定形状，因此需要多个天线阵元构成阵列天线。阵列天线利用电磁波在空间相互干涉原理，构成不同形状阵列。
阵列天线的阵元数目、阵元间距、分布形式、激励相位和幅度5个因素决定了阵列天线波束方向图的形成，决定天线的辐射特征。辐射方向图可以描绘天线辐射特性随空间方向坐标变化关系。
阵列天线原理：叠加原理应用于阵列天线的远区辐射场。
假设一个阵列天线，由$M$个阵元组成，第$m$个阵元在阵中的方向图为$f_m(\varphi ,\theta )$，则整个阵列的方向图可以表示成
$$F(\varphi ,\theta )=\sum _{m=1}^M{f}_m(\varphi ,\theta )S_m$$

若每个阵元的$f_m(\varphi ,\theta )$相同，则上式可以表示为
$$F(\varphi ,\theta )=f(\varphi ,\theta )S$$

式中$f_m(\varphi ,\theta )$也称为阵元因子，$S$表示为阵列因子，它和天线阵元在阵列中所处的位置有关。

设共有$M$个阵列天线阵元，第$m$个阵元在阵列中的位置为$(x_m,y_m,z_m)$，它的场强辐射方向图为$f_m(\varphi ,\theta )$，每个天线阵元的相位与幅度加权系数分别为${\alpha }_m$和$A_m$，复加权系数${\omega }_m$可以表示为
$${\omega }_m=A_m{e}^{-j{\alpha }_m}$$

则整个阵列所有天线阵元在$(\varphi ,\theta )$方向上的方向图可以表示为
$$F(\varphi ,\theta )=\sum _{m=1}^M{\omega }_m\cdot f_m(\varphi ,\theta )\frac{e^{-j\frac{2\pi }{\lambda }{R}_m}}{R_m}$$

$R_m=R-\Delta R_m$，$\Delta R_m$是第$m$个天线阵元到目标的距离与参考点$O$到目标距离之间的差值，上式可以改写为
$$F(\varphi ,\theta )=\sum _{m=1}^M{f}_m(\varphi ,\theta )A_m{e}^{j(\frac{2\pi }{\lambda }\Delta R_m-{\alpha }_m)}$$

均匀直线阵列方向图

假定天线阵元方向图$f(\varphi ,\theta )$足够宽，满足全向性，在线阵天线波束扫描范围内可忽略其影响，即$f(\varphi ,\theta )=1$；天线照射口径函数为等幅分布，即幅度加权系数$A_m=1$，满足均匀分布。线阵天线方向图函数可简化表示为
$$F(\theta )=\sum _{m=0}^{N-1}{e}^{j\frac{2\pi }{\lambda }{d}_m(\sin \theta -\sin {\theta }_0)}$$

用MATLAB仿真：
设一直线阵列由20个阵元按半倍波长等间隔排列组成，所有阵元等幅全向，波长为1m，即阵列孔径为9.5m，天线波束指向为$0^{\circ }$。

均匀平面阵列方向图

天线阵列位于$yoz$平面上，共有$M\times N$个天线阵元形成矩形栅格阵的平面阵列。平面阵列的方向图函数可以表示为：
$$\begin{array}{rl}F(\varphi ,\theta )& =\sum _{n=0}^{N-1}\sum _{m=0}^{M-1}{f}_{mn}(\varphi ,\theta )A_{mn}{e}^{j(\Delta {\varphi }_{mn}-{\alpha }_{mn})}\\ & =\sum _{n=0}^{N-1}\sum _{m=0}^{M-1}{f}_{mn}(\varphi ,\theta )A_{mn}{e}^{j\frac{2\pi }{\lambda }[d_m(\cos \theta \sin \varphi -\cos {\theta }_0\sin {\varphi }_0)+d_n(\sin \theta -\sin {\theta }_0)]}\end{array}$$

通常情况下，天线照射口径函数等幅分布，即幅度加权系数$A_{mn}=1$，满足均匀分布；假定天线阵列方向图$f_{mn}(\varphi ,\theta )$满足全向性，在线阵天线波束扫描范围内可忽略其影响，即$f_{mn}(\varphi ,\theta )=1$，则平面阵列天线的方向图函数可表示为
$$\begin{array}{rl}F(\varphi ,\theta )& =\sum _{n=0}^{N-1}\sum _{m=0}^{M-1}{e}^{j\frac{2\pi }{\lambda }[d_m(\cos \theta \sin \varphi -\cos {\theta }_0\sin {\varphi }_0)+d_n(\sin \theta -\sin {\theta }_0)]}\\ & =\sum _{m=0}^{M-1}{e}^{j\frac{2\pi }{\lambda }{d}_m(\cos \theta \sin \varphi -\cos {\theta }_0\sin {\varphi }_0)}\sum _{n=0}^{N-1}{e}^{j\frac{2\pi }{\lambda }{d}_n(\sin \theta -\sin {\theta }_0)}\\ & =|F_1(\varphi ,\theta )|\cdot |F_2(\theta )|\end{array}$$

$|F_1(\varphi ,\theta )|$表示水平方向线阵的天线方向图，$|F_2(\theta )|$表示垂直方向线阵的天线方向图。

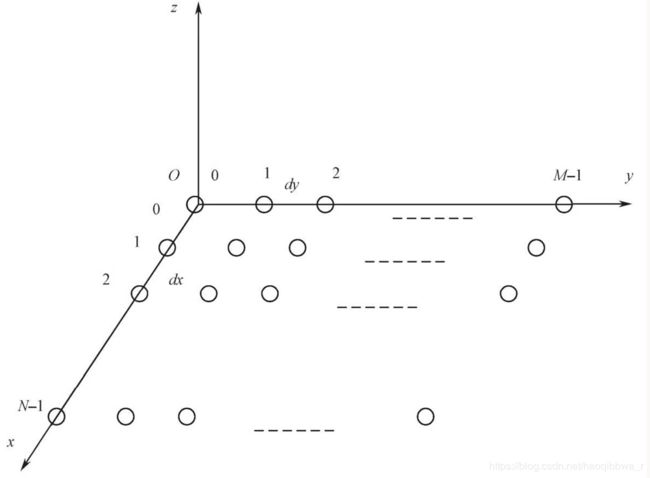
天线阵列位于$xoy$平面上，共有$M\times N$个天线阵元形成矩形栅格阵的平面阵列。平面阵列的方向图函数可以表示为：
$$\begin{array}{rl}F(\varphi ,\theta )& =\sum _{n=0}^{N-1}\sum _{m=0}^{M-1}{e}^{j\frac{2\pi }{\lambda }[d_n(\sin \theta \cos \varphi -\sin {\theta }_0\cos {\varphi }_0)+d_m(\sin \theta \sin \varphi -\sin {\theta }_0\sin {\varphi }_0)]}\\ & =\sum _{m=0}^{M-1}{e}^{j\frac{2\pi }{\lambda }{d}_m(\sin \theta \sin \varphi -\sin {\theta }_0\sin {\varphi }_0)}\sum _{n=0}^{N-1}{e}^{j\frac{2\pi }{\lambda }{d}_n(\sin \theta \cos \varphi -\sin {\theta }_0\cos {\varphi }_0)}\\ & =|F_1(\varphi ,\theta )|\cdot |F_2(\varphi ,\theta )|\end{array}$$

$|F_1(\varphi ,\theta )|$表示$y$方向线阵的天线方向图，$|F_2(\varphi ,\theta )|$表示$x$方向线阵的天线方向图。

用MATLAB仿真：
设一均匀平面阵列由20行方位向阵元和10列俯仰向阵元按半倍波长等间隔排列组成，所有阵元等幅全向，波长为1m，即阵列孔径为9.5m×4.5m，天线波束指向为$(0^{\circ },0^{\circ })$。