线性代数【一】：行列式的概念与计算

本节为线性代数复习笔记的第一部分，行列式的概念与计算，主要包括：行列式的几何意义，行列式的展开计算（余子式，代数余子式），行列式的性质，特殊的五个行列式以及克拉默法则。

1. 行列式的几何意义

  $\left|\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right|$表示平行四边形的面积，记${\alpha }_1=[a_{11},a_{12}]$，${\alpha }_2=[a_{21},a_{22}]$，如下图所示，两个向量所成平行四边形为OABC：

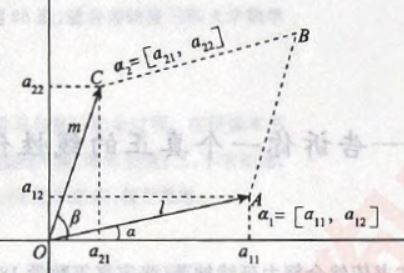
  二阶行列式的值即为该平行四边形的面积，推导如下：

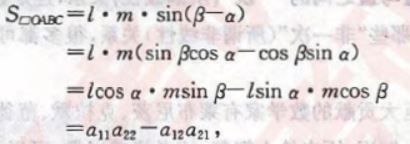
  同理，三阶行列式可以表示平行六面体的体积。

2. 行列式展开计算

2.1 余子式

  n阶行列式中，去掉元素$a_{ij}$所在的第$i$行第$j$列的元素，由剩下的元素按原来的位置与顺序组成的n-1阶行列式称为元素$a_{ij}$的余子式，记为$M_{ij}$。

2.2 代数余子式

  $A_{ij}=(-1{)}^{i+j}{M}_{ij}$

2.3 行列式展开式

  |A|=$\{\begin{array}{l}{a}_{i1}{A}_{i1}+a_{i2}{A}_{i2}+...+a_{in}{A}_{in}\\ ={\Sigma }_{j=1}^n{a}_{ij}{A}_{ij}(按行展开)\\ a_{1j}{A}_{1j}+a_{2j}{A}_{2j}+...+a_{nj}{A}_{nj}\\ ={\Sigma }_{i=1}^n{a}_{ij}{A}_{ij}(按列展开)\end{array}$
  【计算时应令某行/列出现尽可能多的零】

3. 行列式的七个性质

• 行列互换，行列式值不变，即|A|=|A^T|
• 行列式某行/列元素全为0，行列式值为0
• 行列式某行/列元素有非零公因子k，可将k提到行列式外
• 行列式某行/列元素均是两个元素之和，可将行列式拆为两个行列式之和
• 行列式某两行/列互换，行列式值反号
• 行列式某两行/列元素相等或成比例，行列式值为0
• 行列式某行/列的k倍加到另一行/列，行列式值不变

4.五个特殊的行列式

4.1 上/下三角行列式

$\left|\begin{array}{cccc}{a}_{11}& 0& ...& 0\\ a_{11}& a_{22}& ...& 0\\ ...& ...& ...& ...\\ a_{n1}& a_{n2}& ...& a_{nn}\end{array}\right|=\left|\begin{array}{cccc}{a}_{11}& a_{12}& ...& a_{1n}\\ 0& a_{22}& ...& a_{2n}\\ ...& ...& ...& ...\\ 0& 0& ...& a_{nn}\end{array}\right|$
  $=\left|\begin{array}{cccc}{a}_{11}& & & \\ & a_{22}& & \\ & & ...& \\ & & & a_{nn}\end{array}\right|={\prod }_{i=1}^n{a}_{ii}$

4.2 副对角线行列式

$\left|\begin{array}{cccc}{a}_{11}& a_{12}& ...& a_{1n}\\ a_{11}& a_{22}& ...& 0\\ ...& ...& ...& ...\\ a_{n1}& 0& ...& 0\end{array}\right|=\left|\begin{array}{cccc}0& 0& ...& a_{1n}\\ 0& 0& ...& a_{22}\\ ...& ...& ...& ...\\ a_{n1}& a_{n,2}& ...& a_{nn}\end{array}\right|$
  $=\left|\begin{array}{cccc}& & & a_{1n}\\ & & a_{2，n-1}& \\ & & ...& \\ a_{n1}& & & \end{array}\right|$

4.3 特殊的拉普拉斯展开式

$\left|\begin{array}{cc}{A}_{m\times m}& O\\ O& B_{n\times n}\end{array}\right|=\left|\begin{array}{cc}A& C\\ O& B\end{array}\right|=$$\left|\begin{array}{cc}A& O\\ C& B\end{array}\right|=|A||B|$

$\left|\begin{array}{cc}O& A_{n\times n}\\ B_{m\times m}& O\end{array}\right|=\left|\begin{array}{cc}C& A\\ B& O\end{array}\right|=\left|\begin{array}{cc}O& A\\ B& C\end{array}\right|=(-1{)}^{mn}|A||B|$

4.4 范德蒙行列式

$\left|\begin{array}{ccccc}{x}_1^0& x_2^0& ...& x_n^0& \\ x_1^1& x_2^1& ...& x_n^1& \\ ...& ...& ...& ...& \\ x_1^{n-1}& x_2^{n-1}& ...& x_n^{n-1}& \end{array}\right|={\prod }_{1\le i\le j\le n}(x_j-x_i)$

4.5 行和相等行列式

$\left|\begin{array}{ccccc}a& b& b& ...& b\\ b& a& b& ...& b\\ ...& ...& ...& ...& ...\\ b& b& b& ...& a\end{array}\right|=[a+(n-1)b](a-b{)}^{n-1}$
  推导的话，可以将1~n-1行都加到最后一行，提公因数[a+(n-1)b]，然后把最后一行的-1倍逐一加到各行，将行列式按第一行展开。

5. 抽象型计算

$eg.$${\alpha }_1,{\alpha }_2,{\alpha }_3,\beta ,\gamma 均为4维列向量，且|\gamma ,{\alpha }_1,{\alpha }_2,{\alpha }_3|=n$，$|{\alpha }_1,\beta +\gamma ,{\alpha }_2,{\alpha }_3|=m，则|{\alpha }_1,{\alpha }_2,{\alpha }_3,3\beta |=\_\_\_$.
  $解：|{\alpha }_1,{\alpha }_2,{\alpha }_3,3\beta |=3|{\alpha }_1,{\alpha }_2,{\alpha }_3,\beta |=3[|{\alpha }_1,\beta +\gamma ,{\alpha }_2,{\alpha }_3|+|\gamma ,{\alpha }_1,{\alpha }_2,{\alpha }_3|]=3(m+n)$
（行列式列互换，值反号）

6. 克拉默法则

  由n个方程n个未知量构成的非齐次线性方程组：
$$\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+...+a_{1n}{x}_n=b_1\\ a_{21}{x}_1+a_{22}{x}_2+...+a_{2n}{x}_n=b_2\\ ...\\ a_{n1}{x}_1+a_{n2}{x}_2+...+a_{nn}{x}_n=b_n\end{array}$$

  若该方程组的系数行列式|A|$\ne 0$，则方程组有唯一解:
$$x_i=\frac{|A_i|}{|A|}$$

  $|A_i|$表示|A|中第i列元素替换成常数项$b_1,b_2,...,b_n$之后所构成的行列式。

  推论： 由n个方程n个未知量构成的齐次线性方程组：
$$\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+...+a_{1n}{x}_n=0\\ a_{21}{x}_1+a_{22}{x}_2+...+a_{2n}{x}_n=0\\ ...\\ a_{n1}{x}_1+a_{n2}{x}_2+...+a_{nn}{x}_n=0\end{array}$$

  若该方程组的系数行列式|A|$\ne 0$，则方程组有唯一零解。若有非零解，则|A|=0。

---

欢迎扫描二维码关注微信公众号 深度学习与数学   [每天获取免费的大数据、AI等相关的学习资源、经典和最新的深度学习相关的论文研读，算法和其他互联网技能的学习，概率论、线性代数等高等数学知识的回顾]