算法竞赛入门经典------浮点数整数在内存中的存储方式

算法竞赛入门经典---浮点数整数在内存中的存储方式

参考文章：http://www.cnblogs.com/zxtp/p/4938742.html

1、数据的存储方式：大端模式和小端模式

大端模式：低地址位存储值的高位，高地址位存储值的低位 ，数据填写时，不要考虑对应关系，只需要把内存地址从左到右按照由低到高的顺序写出，把值按照通常的高位到低位的顺序写出，两者对照，一个字节一个字节的填充进去。

小端模式：低地址存储值的低位，高地址存储值的高位 ，低位值小放在内存地址小的地方，高位值放在内存地址大的地方。

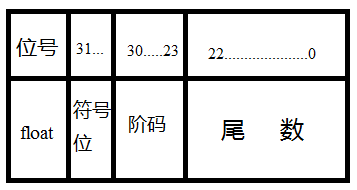
2、浮点数在内存中的存储方式

（1）程序1

#include
int main()
{
	printf("%.1f\n", 8/5);
	return 0;
}

运行结果为

（2）程序2

#include
int main()
{
	printf("%f\n",5);
	return 0;
}

运行结果为

（2）程序2

#include
int main()
{
	int a=5;
	float b=133.5f;
	return 0;
}

解释：

数据在内存中是以二进制的形式存储的。浮点的存储方式与整数区别就是：在二进制科学表示法中，S=M*2^N ，浮点的存储方式是采用：符号位+阶码(N)+尾数(M)的形式。

符号位：在计算机内存中，通常都是以一位表示正数（用0表示）或者负数（用1表示）

阶码：在机器中表示一个浮点数时需要给出指数，这个指数用整数形式表示，这个整数叫做阶码，阶码指明了小数点在数据中的位置。它与科学计数法中的幂是一个道理。

尾数：指小数点后面的数

对于float型数据，其二进制有32位，其中符号位1位，阶码8位，尾数23位。

例子：

将133.5f化为二进制数：

（1）首先将整数部分化为二进制数为：

        1000 0101

（2）然后将小数部分化为二进制为 0.1 。则133.5的二进制数为

        1000 0101.1

而在计算机中是怎么样存储这个数的呢？

首先将这个二进制数用“科学计数法”的形式表示出来就是：

        1. 0000 1011 * 2^7

这里阶码采用移码表示，对于float型数据其规定偏置量为127，阶码位数为8位（对于双精度来说，其规定的偏置量为1023。阶码位数为11位。）,也就是说这里的阶码应该为127+7 = 134。将其化为二进制数为：

           1000 0110

由于规定小数点前面都为1，因此在计算机中，将不会存储小数点前面的1。这里的尾数就为 00001011 。其后全部补0，将其补充到23位。这里是正数，所以符号位为0。

在存储时，符号位在最前面，其次是阶码，最后放尾数。因此数字在内存中存储为：

        0 100 0011 0 000 0101 1000 0000 0000 0000

其十六进制表示为：

        0x 43 05 80 00

则在内存中存放方式为：
低地址-------->高地址

00 80 05 43

测试代码：

#include 
int main()
{
    float num = 133.5f;
    int *p = (int *)#
    printf("0x%x\n", *p);
    return 0;
}

运行结果：

3、整数在内存中的储存形式

整数在内存中是以补码的形式存放

（1）求正数补码

原码：最高位为符号位（0为正，1为负）。

反码：一个正数，它的反码和原码相同；一个负数，符号位为1，其他各位与原码相反。

正数补码：正数的原码、反码和补码都相同。

十进制的整数5，其二进制数为：0000 0000 0000 0000 0000 0000 0000 0101，其补码为0000 0000 0000 0000 0000 0000 0000 0101

（2）求负数补码

负数转化为二进制：求负整数绝对值的二进制数，然后对其求反，求反后再加1得到负整数的二进制。

求十进制数-201的二进制：

201（十进制）---->:0000 0000 0000 0000 0000 0000 1100 1001----->(求反)1111 1111 1111 1111 1111 1111 0011 0110------>(加1)1111 1111 1111 1111 1111 1111 0011 0111

-201(十进制)---->1111 1111 1111 1111 1111 1111 0011 0111（二进制）

负数的反码：其绝对值的所有位取反

负数的补码：它的反码加1

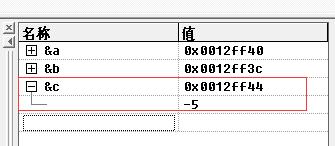
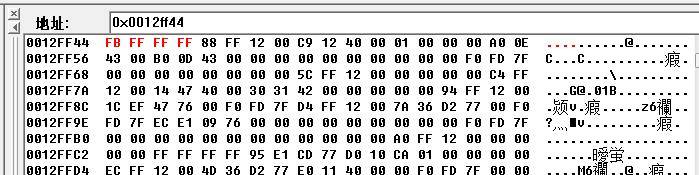
例子：求十进制的整数-5的补码

5的原码：0000 0000 0000 0000 0000 0000 0000 0101

反码：1111 1111 1111 1111 1111 1111 1111 1010

加1得到补码：1111 1111 1111 1111 1111 1111 1111 1011

-5的补码为：1111 1111 1111 1111 1111 1111 1111 1011

补码的十六进制为：FFFF FFFB