静态分析之数据流分析与 SSA 入门 （二）

什么是静态单赋值 SSA

SSA 是 static single assignment 的缩写，也就是静态单赋值形式。顾名思义，就是每个变量只有唯一的赋值。

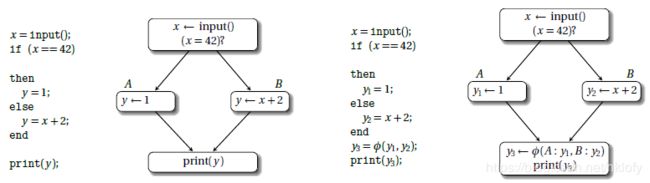
以下图为例，左图是原始代码，里面有分支， y 变量在不同路径中有不同赋值，最后打印 y 的值。右图是等价的 SSA 形式，y 变量在两个分支中被改写为 y1, y2，在控制流交汇处插入 Ф 函数，合并了来自不同边的 y1, y2 值, 赋给 y3, 最后打印的是 y3。

图1 原始代码与 SSA 形式及相应 CFG 控制流图

总结 SSA 形式的两个特征就是：

1. 旧变量按照活动范围（从变量的一次定义到使用）分割，被重新命名为添加数字编号后缀的新变量，每个变量只定义一次。
2. 控制流交汇处有 Ф 函数将来自不同路径的值合并。 Ф 函数表示一个 parallel 操作，根据运行的路径选择一个赋值。如果有多个 Ф 函数，它们是并发执行的。 

这里引入两个名词 use-def chain 和 def-use chain。use-def chain 是一个数据结构，包含一个 def 变量，以及它的全部 use 的集合。相对的，def-use chain 包含一个 use 变量，以及它的全部 def 的集合。以图2左图为例，虚线就是 x 每处定义的 def-use chain. 传统代码因为变量不止一次定义，所以每个定义的 def-use chain 非常复杂。再看右图，SSA 形式下没有同名变量，每个变量只定义一次，所以同名的 use 都是属于它的 def-use chain.  而且因为每个变量 use 前都只有一次 def, 所以 use-def chain 是一对一的。可见，SSA 形式下的 def-use chain 与 use-def chain 都得到了简化。

图2 两种形式下的 Def-use chain

SSA 形式的优点不仅在于简化 def-use chain 与 use-def chain，它提供了一种稀疏表示的数据结构，极大方便了数据流分析。如图3 所示，左边是传统的基于方程组的数据流分析，右边是基于 SSA 形式的数据流分析。前文讲过传统数据流分析是在基本块上沿控制流路径或逆向迭代传播，SSA 形式的 def-use chain 与 use-def chain 直接给出了更多信息，数据流值传播不局限于控制流路径。可见 SSA 形式可以简化数据流分析。

图3 迭代数据流分析与基于 SSA 形式的数据流分析

SSA 的几种类型

SSA 有几种不同风格

最小 SSA

最小静态单赋值形式 (minimal SSA) 有以下特点：同一原始名字的两个不同定义的路径汇合处都插入一个 Ф 函数。这样得到符合两大特征的且拥有最少 Ф 函数数量的 SSA 形式。但是这里的最小不包含优化效果，比如死代码消除，或者值有可能经 live-range 分析是死（参考上篇数据流分析内容）的。

剪枝 SSA

如果变量在基本块的入口处不是活跃 (live) 的，就不必插入 Ф 函数。一种方法是在插入 Ф 函数的时候计算活跃变量分析。另一种剪枝方式是在最小 SSA 上做死代码消除，删掉多余的 Ф 函数。

半剪枝 SSA

鉴于剪枝 SSA 的成本，可以稍微折衷一点。插入 Ф 函数前先去掉非跨越基本块的变量名。这样既减少了名字空间也没有计算活跃变量集的开销。

严格 SSA

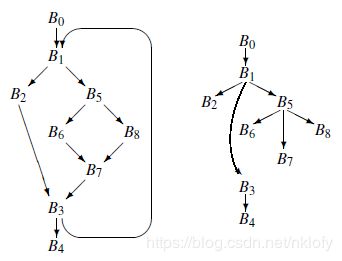
首先引入一个名词叫支配。如果从程序入口到一个结点 A 的所有路径，都先经过结点 B，则称 A 被 B 支配。如果 A 不等于 B，则称 A 被 B 严格支配，A 的支配结点集记为 Dom(A)，Dom(A) 中与 A 最接近的结点称为直接支配结点，记为 IDom(A)。如下图所示，B0 支配 B1，B1 支配 B2, B5... 支配关系是可传递的，例如 B0 也支配 B2, B5... 这样可以根据支配关系构造一棵树，路径上的父结点直接支配子结点，根结点支配所有后代结点。

图4 支配树

如果一个 SSA 具有以下特点：每个 use 被其 def 支配，那么称为严格 SSA。如下图所示，左图 a, b 的 def 没有支配 use，所以不是严格 SSA。在右图中，汇合点插入2个 Ф 函数，重新编号了变量，保证了支配性。其中 ⊥ 表示未定义。

图5 严格 SSA

传统与变形 SSA

构造 Ф-web 并查集，将 def-use chains 有相同变量的都连接起来得到一个网络，比如 Ф 函数两边的 define 或 parameter 变量。可以得到若干网络。传统 SSA 的特点是 Ф-web 中变量的 live-range 互相不干涉。传统 SSA 经过优化例如复制传播之后，可能会被破坏这个性质，就称为变形 SSA。

SSA 构造算法

这里介绍一种基于支配边界的 SSA 构造算法。这个算法分为两个步骤：1，在支配边界插入 Ф 结点；2，变量重命名。 

计算支配边界的目的是只在需要的地方插入 Ф 结点，支配边界的定义是：A 支配 B 的一个前驱但不严格支配 B，则称 B 为 A 的支配边界。A 的所有支配边界组成的集合记为 DF(A)。DF 即 dominace frontier。

图6 计算 DF 图

计算支配边界的方法如图6. 左图是控制流图。首先构造出支配树。中图是一棵支配树，从父结点到子结点的边是支配边。控制流路径除了支配边，就是汇合边，例如 D 到 E，F 到 G。首先汇合边的目的结点就是起点的支配边界。例如 E 是 D 的支配边界，F 是 G 的支配边界。然后将汇合边的起点向其直接支配点移动，例如 D 移动到 C，若 C 不是 E 的支配结点，则 E 也是 C 的支配边界，以此类推。最右图则表示最终计算结果，每个箭头指向结点是起点的支配边界。算法伪码如下：

```

for node in all nodes of CFG

    if n has multiple predecessors

        for each predecessor p of n

            runner = p

            while runner != IDom(n)

                add n to DF(runner)

                runner = IDom(runner)

```

计算完成支配边界后基本块 b 中对 x 定义，则在 DF(b) 内每个结点起始处放置一个 Ф 函数。放置过 Ф 函数的基本块其 DF 也要继续放置 Ф 函数。

最后是变量重命名。

每个全局名（对应半剪枝类型，即不考虑不跨越基本块的变量）变成一个基本名，对其各个定义添加数字编号。例如 x，对第一个定义命名为 x1，第二个定义命名为 x2... 方法是在支配树上先序遍历，在每个块上首先重命名 Ф 函数的定义，然后依次访问各条指令，用当前 SSA 名重写各操作数，并为操作的结果创建一个新的 SSA 名。然后使用当前 SSA 名改写后继块 Ф 函数的参数。最后对支配树的子结点递归处理。返回后将 SSA 名恢复前一个状态。所以这里可以用每变量一个栈来存放 SSA 名，压栈时 SSA 名的编号递增，处理完一个基本块后本块内生成名全部出栈。 伪代码如下：

```

NewName(n)

    i = counter[n]

    counter[n] ++

    push i onto stack[n]

    return "ni"

Rename(b)

    for each Ф-function "x = Ф(...)", rewrite x as NewName(x)

    for each operation "x = y op z", rewrite y as top(stack[y]), rewrite z as top(stack[z]), rewrite x as NewName(x)

    for each successor of b in CFG, fill in Ф-funcitons

    for each successor s of b in dominator tree, Rename(s)

    popstack[x]

``` 

SSA 解构算法

处理器不能处理 Ф 函数，所以我们需要将 SSA 形式转换回可执行代码，这就是 SSA 解构。

SSA 解构是去掉 Ф 函数的操作，但是需要增加一些复制。例如  xi = Ф(xj, xk)，去掉这一条语句后应该沿着传入 xj 的边插入 xi = xj，沿着传入 xk 的边插入 xi = xk，就能保证执行正确。但这里面有几种特殊情况：

关键边 critical edge

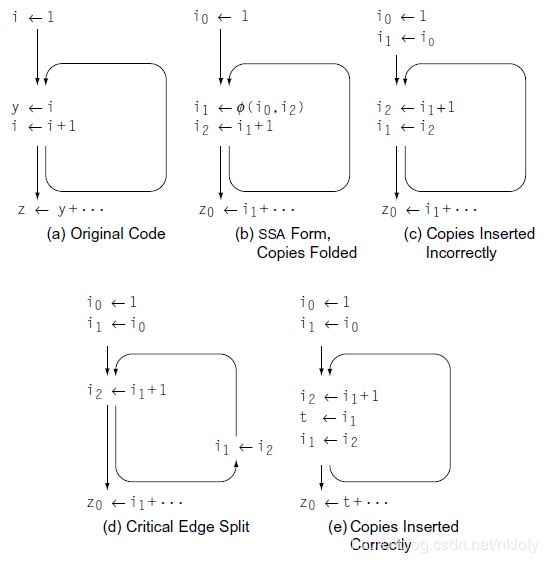
边的源结点有多个后继，目标结点有多个前驱，则称为关键边。这种情况需要拆分关键边，在关键边里面增加一个基本块，并将复制操作放在这个基本块里。以下图为例。图 (a) 到 图 (b) 是构造 SSA 后进行复制折叠的优化。图 (c) 是插入复制不正确的例子。i1 的 Ф 删除后，在前继块插入复制。但是另一条后继路径上给 z0 赋值时 i1 的值却不正确。如果按照图 (d) 所示，拆分关键边后复制就是正确的。

图7 关键边拆分

丢失复制问题 lost-copy

仍然以图7 为例，如果无法拆分关键边。那么就出现了图 (c) 的复制丢失问题。有一种解法是分析复制操作的目标，如果是活动状态，则建立一个临时变量，重写后续引用。例如图 (e) 所示。

交换问题 swap

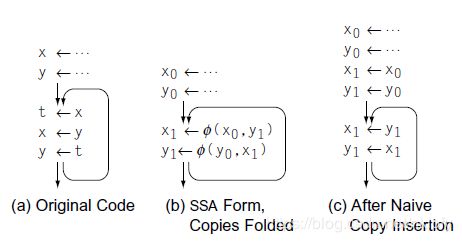
 在语义上要求同一基本块内的 Ф 函数并发执行。图 (c) 是解构 SSA 后插入复制操作的结果。因为操作不是并发而是顺序执行的，x1, y1 的交换失败了。这个问题的解法是分析 Ф 函数有没有引用同一基本块其他 Ф 函数的结果，对于引用形成的环则必须插入临时变量。

图8 交换问题

这些特殊 case 其实并不容易遇到，往往是复制折叠优化等代码被重排和改变的操作之后才会出现。如果是新建的 SSA，则不会有这种问题。

以上是对 SSA 算法的简单总结。例子与图引用自《static single assignment book》与 《engineering a compiler》。