python多继承---C3算法
一、基本概念
1. mro序列
MRO是一个有序列表L,在类被创建时就计算出来。
通用计算公式为:
mro(Child(Base1,Base2)) = [ Child ] + merge( mro(Base1), mro(Base2), [ Base1, Base2] )
(其中Child继承自Base1, Base2)
如果继承至一个基类:class B(A)
这时B的mro序列为
mro( B ) = mro( B(A) )
= [B] + merge( mro(A) + [A] )
= [B] + merge( [A] + [A] )
= [B,A]
如果继承至多个基类:class B(A1, A2, A3 …)
这时B的mro序列
mro(B) = mro( B(A1, A2, A3 …) )
= [B] + merge( mro(A1), mro(A2), mro(A3) ..., [A1, A2, A3] )
= ...
计算结果为列表,列表中至少有一个元素即类自己,如上述示例[A1,A2,A3]。merge操作是C3算法的核心。
2. 表头和表尾:
表头:
列表的第一个元素
表尾:
列表中表头以外的元素集合(可以为空)
示例
列表:[A, B, C]
表头是A,表尾是B和C
3. 列表之间的+操作
+操作:
[A] + [B] = [A, B]
(以下的计算中默认省略)
3. merge操作:
-
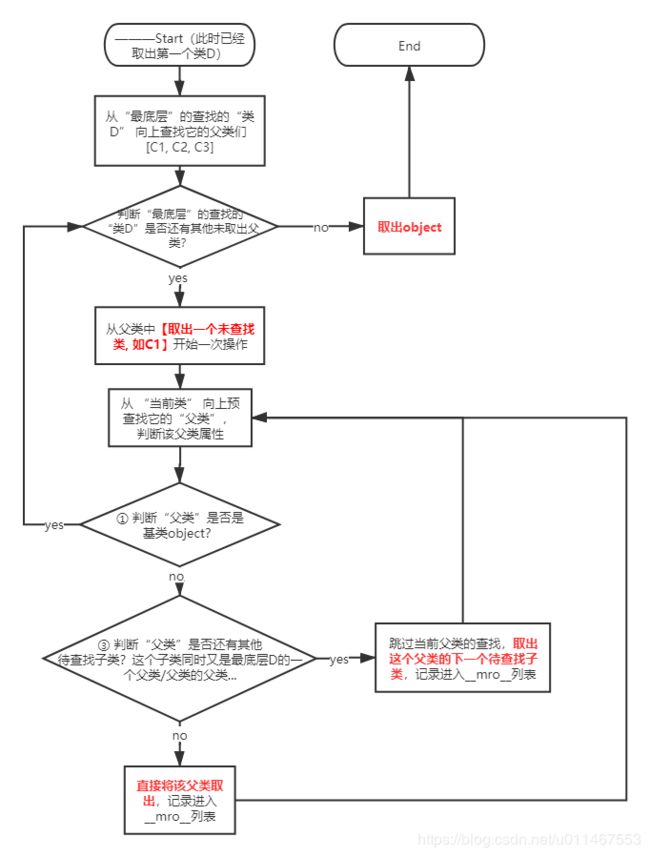
merge操作流程图:
merge操作示例:
如计算merge( [E,O], [C,E,F,O], [C] )
有三个列表 : ① ② ③
1 merge不为空,取出第一个列表列表①的表头E,进行判断
各个列表的表尾分别是[O], [E,F,O],E在这些表尾的集合中,因而跳过当前当前列表
2 取出列表②的表头C,进行判断
C不在各个列表的集合中,因而将C拿出到merge外,并从所有表头删除
merge( [E,O], [C,E,F,O], [C]) = [C] + merge( [E,O], [E,F,O] )
3 进行下一次新的merge操作 ......
二、实战测试
1. 计算实例1
示例:(多继承UML图,引用见参考)
备注:O==object
如何计算mro(A) ?
mro(A) = mro( A(B,C) )
原式= [A] + merge( mro(B),mro(C),[B,C] )
mro(B) = mro( B(D,E) )
= [B] + merge( mro(D), mro(E), [D,E] ) # 多继承
= [B] + merge( [D,O] , [E,O] , [D,E] ) # 单继承mro(D(O))=[D,O]
= [B,D] + merge( [O] , [E,O] , [E] ) # 拿出并删除D
= [B,D,E] + merge([O] , [O])
= [B,D,E,O]
mro(C) = mro( C(E,F) )
= [C] + merge( mro(E), mro(F), [E,F] )
= [C] + merge( [E,O] , [F,O] , [E,F] )
= [C,E] + merge( [O] , [F,O] , [F] ) # 跳过O,拿出并删除
= [C,E,F] + merge([O] , [O])
= [C,E,F,O]
原式= [A] + merge( [B,D,E,O], [C,E,F,O], [B,C])
= [A,B] + merge( [D,E,O], [C,E,F,O], [C])
= [A,B,D] + merge( [E,O], [C,E,F,O], [C]) # 跳过E
= [A,B,D,C] + merge([E,O], [E,F,O])
= [A,B,D,C,E] + merge([O], [F,O]) # 跳过O
= [A,B,D,C,E,F] + merge([O], [O])
= [A,B,D,C,E,F,O]
三、总结
每次判断如何读取都要这么麻烦计算吗?可有简单方法?
我对此做了一个简单总结。
1. 规律总结
如何快速判断查找规律?
简单的八个字总结就是:“从一至顶,有子先出”。
一句话解释就是,从当前查找类的第一个待查找父类一直向上查找,当遇到父类还有其他子类时,且子类也是当前查找类的父类或父父类,则优先查找其子类,直到到达查找顶端Object类(跳过Object类),再查找下一个待查找父类。重复至结束所有查找。