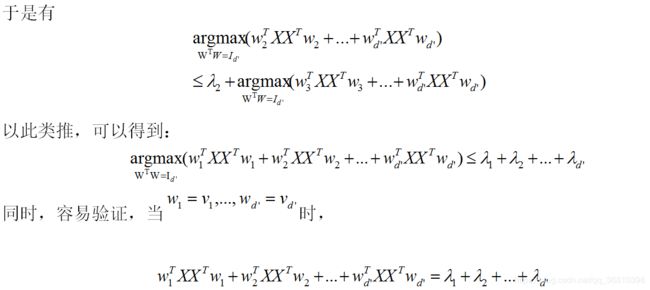主成分分析降维原理——PCA数学推导
文章目录
- 1.PCA降维的计算过程
- 2.数学推导
- 3.总结
1.PCA降维的计算过程
下图是从西瓜书里截取的PCA降维过程的图片。

需要说明的是,算法中的向量为列向量。假设原始维度为d,样本数目为m,因此特征矩阵X的维度为d×m,W的维度为d×d’。降维的时候,transpose(W)*X得到 d’×m的矩阵,它的每一列,即为降维后的向量。
2.数学推导
不过西瓜书里没有详细推导(我查了好几本书,包括DeepLearning和Hands On ML,都没有写详细推导,DeepLearning是作为一个练习让读者自己做)——为什么选取最大的d’个特征值所对应的特征向量就可以组成投影矩阵?结合DeepLearning里的部分过程,我补全了一个类似的证明。不排除有不对的地方,供有需要的朋友参考。
3.总结
(1)通过上述推导,感觉自己应该更清楚了PCA的原理:
PCA的目标是通过降维之后的向量,再还原回来的之后和原向量最接近(都是用线性映射),为了实现这个目标,得到的投影矩阵恰好是,原数据集的协方差矩阵的前d’个主成分为列组成的矩阵。
(2)从上述推导过程,也可以看到PCA和“不含非线性元素的自编码器”是在某些限定之下等价的。这在某些自编码器的资料里也常被提到,它们的思想都是相同的————通过线性编码和解码,使得输入和输出的差尽量小。