Mtaplotlib数据可视化

Mtaplotlib常用技巧

1、导入matplotlib

import matplotlib as mpl
import matplotlib.pyplot as plt

2、设置绘图样式

plt.style.use('classic')

3、一个python会话只能出现一次plt.show()
在IPython Notebook中画图：

%matplotlib notebook会在Notebook中启动交互式图形
%matplotlib inline会在Notebook中启动静态图形

4、将图片保存为文件

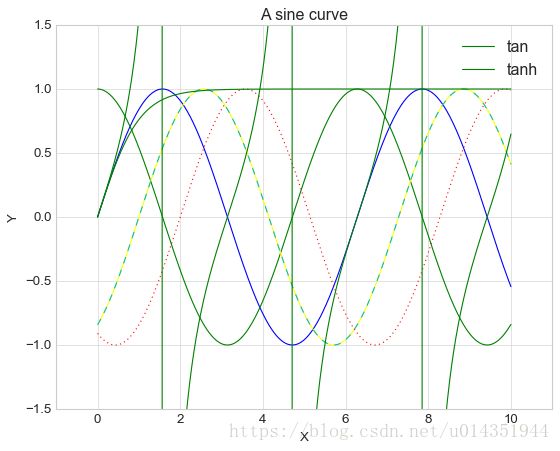
fig.savefig('my_figure.png')

简易线性图

plt.style.use('seaborn-whitegrid')
#创建一个图形fig
fig=plt.figure()
#创建一个坐标轴
ax=plt.axes()
x=np.linspace(0,10,1000)
ax.plot(x,np.sin(x))
plt.plot(x,np.cos(x))
#设置颜色
ax.plot(x,np.sin(x-1),color='yellow')
#调整线条格式，可以使用简写模式如（‘-’，‘--’，‘-.’，‘:’）
ax.plot(x,np.sin(x-2),linestyle='dotted')
#可以将linestyle和color编码组合
ax.plot(x,np.sin(x-1),'--c')

#调整坐标轴的上下线
plt.xlim(-1,11)
plt.ylim(-1.5,1.5)

#设置图形标题、坐标轴标题
plt.title("A sine curve")
plt.xlabel('X')
plt.ylabel('Y')

#设置图例
plt.plot(x,np.tan(x),'-g',label='tan')
plt.plot(x,np.tanh(x),'-g',label='tanh')
plt.legend()

注：（1）plt.axis()通过传入[xmin,xmax.ymin,ymax]对应的值，可以通过一行代码设置x和y的限值，还可以传入字符串参数，如plt.axis(‘tight’)按照图形的内容自动收紧坐标轴。
（2）ax.set()可以一次性设置所有的属性

简易散点图

使用plt.plot()画散点图，具体使用参考https://matplotlib.org/users/pyplot_tutorial.html

x=np.linspace(0,10,30)
y=np.sin(x)
plt.plot(x,y,'o',color='black')
plt.plot(x,np.sin(x-1),'-ok')
plt.plot(x,np.sin(x-2),'-p',color='gray',markersize=15,linewidth=4,markerfacecolor='white',markeredgecolor='gray',markeredgewidth=2)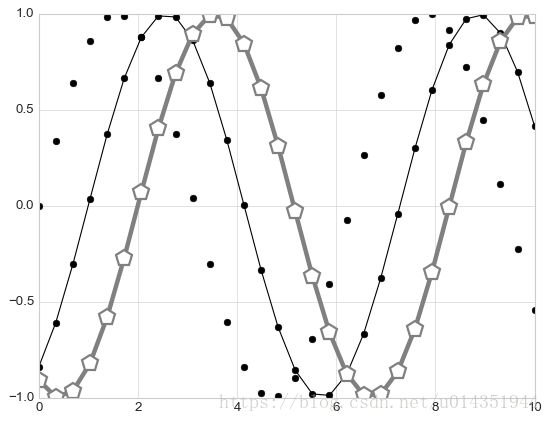

使用plt.scatter画散点图
plt.scatter的简易使用与plt.plot类似，主要的差别在于可以单独控制每个散点与数据匹配，也可以让每个散点具有不同的属性（大小、表面颜色、边框颜色等），alpha参数调剂透明度，cmap设置colormap,参考https://matplotlib.org/examples/color/colormaps_reference.html

rng=np.random.RandomState(0)
x=rng.randn(100)
y=rng.randn(100)
colors=rng.rand(100)
sizes=1000*rng.rand(100)
plt.scatter(x,y,c=colors,s=sizes,alpha=0.3,cmap='viridis')
plt.colorbar()

注：在面对大型数据集的时候，plt.plot方法比plt.scatter更好，因为plt.scatter会对每个散点进行单独的大小和颜色渲染，因此渲染器会消耗更多的资源，而在plt.plot，散点基本都彼此复制，因此整个数据集中所有的点的颜色、尺寸只需要配置一次。

可视化异常处理

1、基本误差线
fmt控制线条和点的外观，语法与plt.plot的缩写代码相同，ecolor和elinesgray控制误差线的颜色和宽度，capsize控制误差线两端的宽度

x=np.linspace(0,10,50)
dy=0.8
y=np.sin(x)+dy*np.random.randn(50)
plt.errorbar(x,y,yerr=dy,fmt='.k',ecolor='lightgray',elinewidth=3,capsize=10)

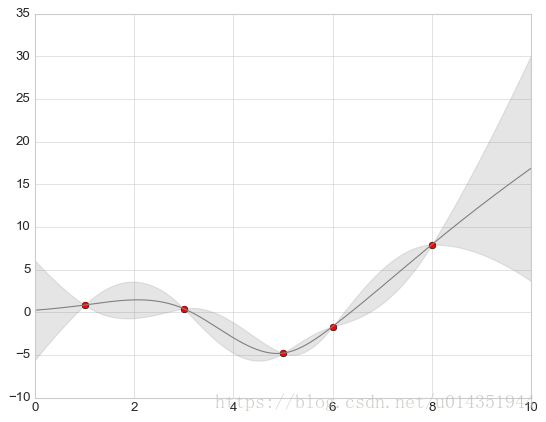
2、连续误差
连续误差可以通过plt.plot和plt.fill_between来解决，fill_betweem函数首先传入x轴坐标，然后传入y轴下边界以及y轴上边界，这样整个却与就被误差线填充了

from sklearn.gaussian_process import GaussianProcess
#定义模型和要画的数据
model=lambda x: x*np.sin(x)
xdata=np.array([1,3,5,6,8])
ydata=model(xdata)
#计算高斯过程拟合结果
gp=GaussianProcess(corr='cubic',theta0=1e-2,thetaL=1e-4,thetaU=1E-1,random_start=100)
gp.fit(xdata[:,np.newaxis],ydata)
xfit=np.linspace(0,10,1000)
yfit,MSE=gp.predict(xfit[:,np.newaxis],eval_MSE=True)
dyfit=2*np.sqrt(MSE)

#将结果可视化
plt.plot(xdata,ydata,'or')
plt.plot(xfit,yfit,'-',color='gray')
plt.fill_between(xfit,yfit-dyfit,yfit+dyfit,color='gray',alpha=0.2)
plt.xlim(0,10);

密度图和等高线图

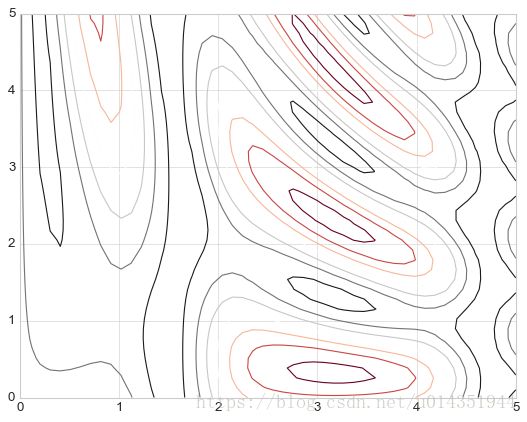
默认虚线表示负数，实线表示正数，可以使用cmap参数设置一个线条配色方案来自定义颜色，colors参数和cmap参数只能设置一个，另外一个为空

def f(x,y):
    return np.sin(x)**10+np.cos(1-+y*x)*np.cos(x)
x=np.linspace(0,5,50)
y=np.linspace(0,5,40)
X,Y=np.meshgrid(x,y)
Z=f(X,Y)
plt.contour(X,Y,Z,colors='black');

plt.contour(X,Y,Z,cmap=plt.cm.RdGy);

#20表示将数据范围等分为20份
plt.contourf(X,Y,Z,20,cmap=plt.cm.RdGy)
plt.colorbar();

由于颜色的变化是一个离散的而非连续的，所以上图不是很满意，这个可以通过plt.imshow()函数来处理，它可以将二位数组渲染成渐变图，但有一些注意事项：
- plt.imshow()不支持用x轴和y轴数据设置网格，而是必须通过extend参数设置图形的坐标范围[xmin,xmax,ymin,ymax]。
- plt.imshow()默认使用标准的图形数组定义，就是原点位于左上角，而不是绝大多数等高线图中使用的左下角。
- plt.imshow()会自动调整坐标轴的精度以适应数据显示，可以通过plt.axis(aspect=’image’)来设置x轴和y轴的单位

plt.imshow(Z,extent=[0,5,0,5],origin='lower',cmap='RdGy')
plt.colorbar()
plt.axis(aspect='image');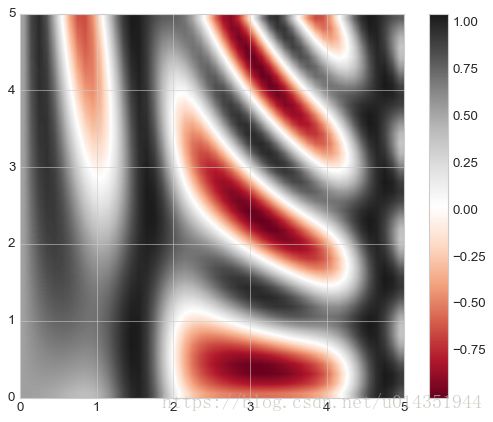

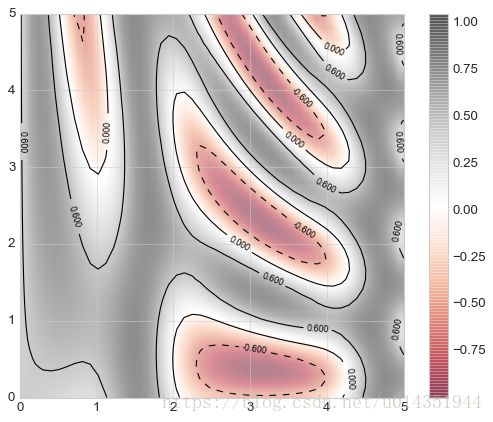
等高线图和彩色图组合，通过alpha参数设置透明度，和另一幅坐标轴、带数据标签的等高线图叠放在一起(plt.clabel()函数实现)

contours=plt.contour(X,Y,Z,3,colors='black')
plt.clabel(contours,inline=True,fontsize=8)
plt.imshow(Z,extent=[0,5,0,5],origin='lower',cmap='RdGy',alpha=0.5)
plt.colorbar();

频次直方图、数据区间划分和分布密度

频次直方图
plt.hist()常用参数
data: 需要计算直方图的一维数组

bins: 直方图的柱数，可选项，默认为10

density: 是否将得到的直方图向量归一化。默认为False

color: 直方图颜色

edgecolor: 直方图边框颜色

alpha: 透明度

histtype: 直方图类型，‘bar’, ‘barstacked’, ‘step’, ‘stepfilled’

data = np.random.randn(1000)
plt.hist(data, bins=30, density=True, alpha=0.5,
         histtype='stepfilled', color='steelblue',
         edgecolor='none');

如果只需要每段区间的样本数，不需要画图，可以使用np.histogram()
二维频次直方图与数据区间划分
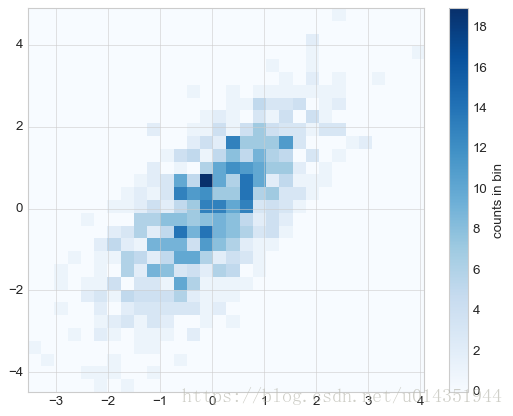
plt.hist2d:

mean=[0,0]
cov=[[1,1],[1,2]]
x,y=np.random.multivariate_normal(mean,cov,1000).T
plt.hist2d(x,y,bins=30,cmap='Blues')
cb=plt.colorbar()
cb.set_label('counts in bin')

np.histogram2d也可以不画图只计算结果

plt.hexbin:

plt.hexbin(x,y,gridsize=30,cmap='Blues')
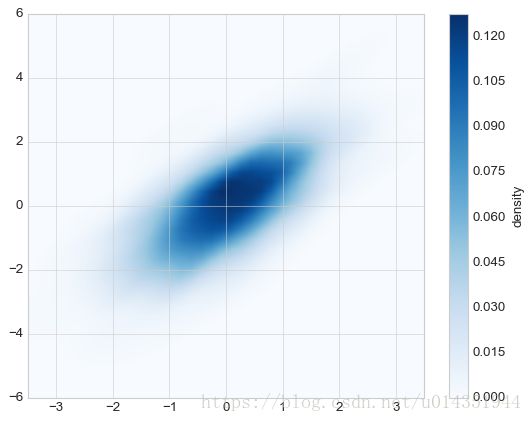
plt.colorbar(label='count in bin');

核密度估计：
kde方法：抹掉空间中离散的数据点，从而拟合出一个平滑的函数

from scipy.stats import gaussian_kde
#拟合数组维度[ndim,nsamples]
data=np.vstack([x,y])
kde=gaussian_kde(data)
#用一堆规则的网格数据进行拟合
xgrid=np.linspace(-3.5,3.5,40)
ygrid=np.linspace(-6,6,40)
Xgrid,Ygrid=np.meshgrid(xgrid,ygrid)
Z=kde.evaluate(np.vstack([Xgrid.ravel(),Ygrid.ravel()]))
plt.imshow(Z.reshape(Xgrid.shape),origin='lower',aspect='auto',extent=[-3.5,3.5,-6,6],cmap='Blues')
cb=plt.colorbar()
cb.set_label('density')

配置图例

plt.legend()创建图例主要参数

参数	功能
loc	设置图例的位置
frameon	设置外边框是否显示
ncol	设置图例的标签列数
fancybox	定义圆角边框
framealpha	改变外框透明度
shadow	增加边框阴影
borderpad	改变文字间距

当需要多个图例的时候的时候可以使用ax。add_artist()添加图例对象

多子图

plt.axes(),可选参数[底坐标，左坐标，宽度，高度]

ax1=plt.axes()
ax2=plt.axes([0.65,0.65,0.2,0.2])

面向对象接口

fig=plt.figure()
ax1=fig.add_axes([0.1,0.5,0.8,0.4],xticklabels=[],ylim=(-1.2,1.2))
ax2=fig.add_axes([0.1,0.1,0.8,0.4],ylim=(-1.2,1.2))
x=np.linspace(0,10)
ax1.plot(np.sin(x))
ax2.plot(np.cos(x))

上制图起点为y坐标为0.5的位置且与下子图x周刻度对应

plt.subplot()

for i in range(1,7):
    plt.subplot(2,3,i)

带有边距调节功能，fig.add_subplot()是plt.subplot的面向对象接口

fig=plt.figure()
fig.subplots_adjust(hspace=0.4,wspace=0.4)
for i in range(1,7):
    ax=fig.add_subplot(2,3,i)

plt.subplots()

fig,ax=plt.subplots(2,3,sharex='col',sharey='row')

共享x轴和y轴

plt.GridSpec：实现更复杂的排列方式

grid=plt.GridSpec(2,3,wspace=0.4,hspace=0.3)
plt.subplot(grid[0,0])
plt.subplot(grid[0,1:])
plt.subplot(grid[1,:2])
plt.subplot(grid[1,2])

使用类似切片的语法设置制图的位置和扩展尺寸

文字和注释

• 添加文字
  ax.text()方法需要一个x轴坐标，一个y轴坐标，一个字符串和一些可选参数，如文字的颜色、字号、风格、对齐方式以及其他文字属性
• 坐标转换：
  ax.transData 以数据为基准的坐标转换
  ax.transAxes 以坐标轴为基准的坐标转换
  fig.transFigure 以图形为基准的坐标变换
• 箭头和注释
  plt.annotate()既可以创建文字也可以创建箭头

fig,ax=plt.subplots()
x=np.linspace(0,20,1000)
ax.plot(x,np.cos(x))
ax.axis('equal')
ax.annotate('local maximum',xy=(6.28,1),xytext=(10,4),arrowprops=dict(facecolor='black',shrink=0.05))
ax.annotate('local minimum',xy=(5*np.pi,-1),xytext=(2,-6),arrowprops=dict(arrowstyle="->",connectionstyle="angle3,angleA=0,angleB=-90"))

自定义坐标轴刻度

每个坐标轴都有主要刻度线和次要刻度线，主要刻度线显示为较大的刻度线和标签，而次要刻度都显示为一个较小的刻度线不显示标签，可以通过设置每个坐标轴的formatter与locator对象，自定义这些刻度属性。

ax=plt.axes()
ax.plot(np.random.rand(50))

ax.yaxis.set_major_locator(plt.NullLocator())
ax.xaxis.set_major_formatter(plt.NullFormatter())

隐藏图形的x轴标签（保留了刻度线和网格线）和y轴刻度

定位器类	描述
NullLocator	无刻度
FixedLocator	刻度位置固定
IndexLocator	用索引作为定位器
LinearLocator	从min到max均匀分布刻度
LogLocator	从min到max按对数分布刻度
MultipleLocator	刻度和范围都是基数的倍数
MaxNLocator	为最大刻度找到最优位置
AutoLocator	以MaxNlocator进行简单配置
AutoMinorLocator	次要刻度的定位器

格式生成器类	描述
NullFormatter	刻度上无标签
IndexFormatter	将一组标签设置为字符串
FixedFromatter	手动为刻度设置标签
FuncFormatter	用自定义函数设置标签
FromatStrFormatter	为每个刻度值设置字符串格式
ScalarFormatter	为标量值设置标签
LogFormatter	对数坐标轴的默认格式生成器

画三维图

1、三维数据点和向

fig = plt.figure()
ax=plt.axes(projection='3d')

#三维线的数据
zline=np.linspace(0,15,1000)
xline=np.sin(zline)
yline=np.cos(zline)
ax.plot3D(xline,yline,zline,'gray')

#三维散点的数据
zdata=15*np.random.random(100)
xdata=np.sin(zdata)+0.1*np.random.randn(100)
ydata=np.cos(zdata)+0.1*np.random.randn(100)
ax.scatter3D(xdata,ydata,zdata,c=zdata,cmap='Greens')

2、三维等高线图

def f(x,y):
     return np.sin(np.sqrt(x**2+y**2))
x=np.linspace(-6,6,30)
y=np.linspace(-6,6,30)
X,Y=np.meshgrid(x,y)
Z=f(X,Y)
fig=plt.figure()
ax=plt.axes(projection='3d')
ax.contour3D(X,Y,Z,50,cmap='binary')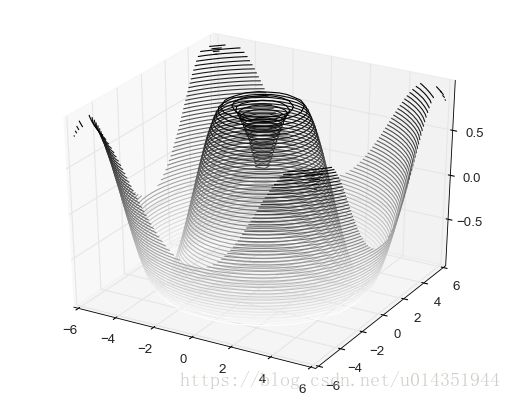

ax.view_init()可以调整观察角度和方位角
3、线框图和曲面图

fig=plt.figure()
ax=plt.axes(projection='3d')
ax.plot_wireframe(X,Y,Z,color='black')

ax=plt.axes(projection='3d')
ax.plot_surface(X,Y,Z,rstride=1,cstride=1,cmap='viridis',edgecolor='none')

画曲面图可以使用极坐标
4、曲面三角剖分

theta=2*np.pi*np.random.random(1000)
r=6*np.random.random(1000)
x=np.ravel(r*np.sin(theta))
y=np.ravel(r*np.cos(theta))
z=f(x,y)
ax=plt.axes(projection='3d')
ax.scatter3D(x,y,z,c=z,cmap='viridis',linewidth=0.5)

三维采样的曲面图，可以使用ax.plot_trisurf进行修补

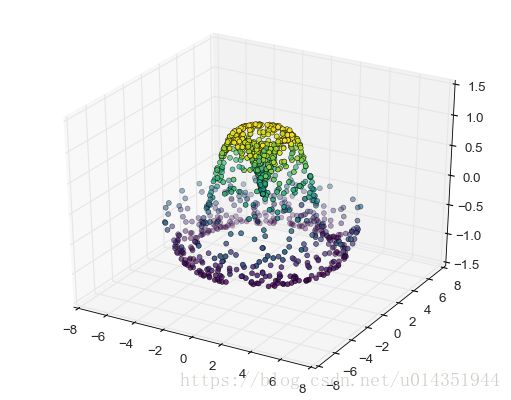
ax=plt.axes(projection='3d')
ax.plot_trisurf(x,y,z,cmap='viridis',edgecolor='none')

Basemap

from mpl_toolkits.basemap import Basemap
plt.figure(figsize=(8,8))
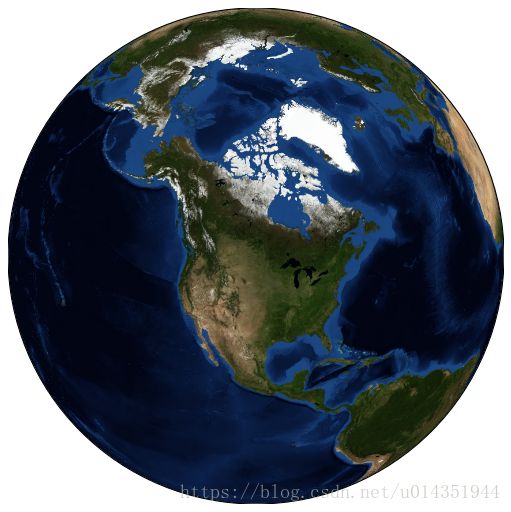
m=Basemap(projection='ortho',resolution=None,lat_0=50,lon_0=-100)
m.bluemarble(scale=0.5)

fig=plt.figure(figsize=(8,8))
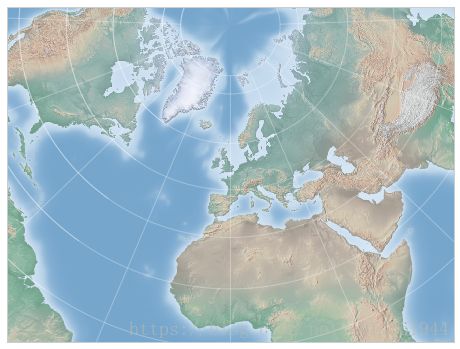
m=Basemap(projection='lcc',resolution=None,width=8e6,height=8e6,lat_0=45,lon_0=-100,)
m.etopo(scale=0.5,alpha=0.5)

x,y=m(-122.3,47.6)
plt.plot(x,y,'ok',markersize=5)
plt.text(x,y,'Seattle',fontsize=12)

Keyword	Description
projection	映射规则
llcrnrlon	所需地图域左下角的经度（度）。
llcrnrlat	所需地图域左下角的纬度（度）。
urcrnrlon	所需地图域右上角的经度（度）。
urcrnrlat	所需地图域右上角的纬度（度）。
width	在投影坐标（米）中期望的地图域的宽度。
height	投影坐标（米）中期望的地图域的高度。
lon_0	center of desired map domain (in degrees).
lat_0	center of desired map domain (in degrees).

地图投影规则
- 圆柱投影
纬度线与经度线分别映射成水平线与竖直线，采用这种投影，赤道区域的显示效果非常好，但是南北极附近的区域会严重变形。圆柱投影类型有圆柱投影(‘cyl’)，墨卡托(‘merc’),投影和圆柱等积(‘cea’)，需要设置llcrnrlon、llcrnrlat、urcrnrlon、urcrnrlat。

from itertools import chain

def draw_map(m, scale=0.2):
    # draw a shaded-relief image
    m.shadedrelief(scale=scale)

    # lats and longs are returned as a dictionary
    lats = m.drawparallels(np.linspace(-90, 90, 13))
    lons = m.drawmeridians(np.linspace(-180, 180, 13))

    # keys contain the plt.Line2D instances
    lat_lines = chain(*(tup[1][0] for tup in lats.items()))
    lon_lines = chain(*(tup[1][0] for tup in lons.items()))
    all_lines = chain(lat_lines, lon_lines)

    # cycle through these lines and set the desired style
    for line in all_lines:
        line.set(linestyle='-', alpha=0.3, color='w')

fig = plt.figure(figsize=(8, 6), edgecolor='w')
m = Basemap(projection='cyl', resolution=None,
            llcrnrlat=-90, urcrnrlat=90,
            llcrnrlon=-180, urcrnrlon=180, )
draw_map(m)

- 伪圆柱投影
伪圆柱投影的经线不在必须是竖直的，这样可以使附近的区域更加真实,这类投影主要有摩尔威德(‘moll’)，正弦(’sinu),罗宾森(‘robin’),该类型投影，有两个额外参数地图中心的纬度(lat_0)和经度(lon_0)

fig=plt.figure(figsize=(8,6),edgecolor='w')
m=Basemap(projection='moll',resolution=None,lat_0=0,lon_0=0)
draw_map(m)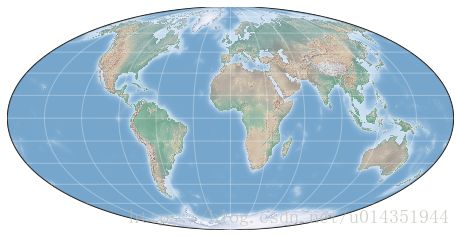

- 透视投影
从某一个透视点对地球进行透视获得的投影，典型的是正射(‘ortho’)，还有球心投影(‘gnom’)和球极平面投影(‘stere’)，这些投影通常用于显示地球较小面积区域

fig=plt.figure(figsize=(8,8),edgecolor='w')
m=Basemap(projection='ortho',resolution=None,lat_0=50,lon_0=0)
draw_map(m)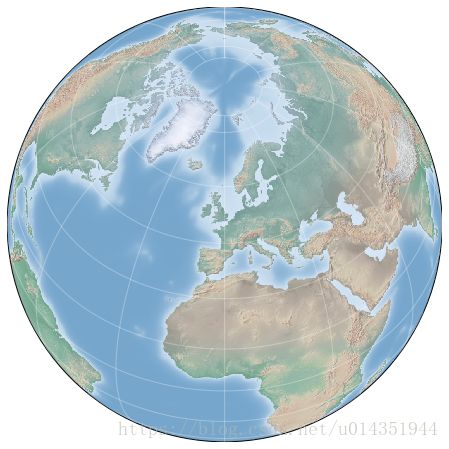

- 圆锥投影
先将地图投影成一个圆锥体，然后再将其展开，典型事例是兰勃特投影(‘lcc’),还有等距圆锥(‘eqdc’)和阿尔博斯等积圆锥(‘aea’)

fig=plt.figure(figsize=(8,8),edgecolor='w')
m=Basemap(projection='lcc',resolution=None,lat_0=50,lon_0=0,lat_1=45,lat_2=55,width=1.6e7,height=1.2e7)
draw_map(m)

绘制地图背景

函数	功能
drawcoastlines	绘制大陆海岸线
drawlsmask	为陆地与海洋设置填充色，从而可以再陆地或海洋投影其它图像
drawmapboundary	绘制地图边界，包括为海洋填充颜色
drawrivers	绘制河流
fillcontinents	用一种颜色填充大陆，用另一种颜色填充胡泊
drawcountries	绘制国界线
drawstates	绘制州界线
drawcounties	绘制县界线
drawgreatcircle	在两点之间绘制一个大圆
drawparallels	绘制纬线
drawmeridians	绘制经线
drawmapscale	在地图上绘制一个线性比例尺
bluemarble	绘制NASA蓝色弹珠地球投影
shadedrelief	在地图上绘制地貌晕渲图
etopo	在地图上绘制地形眩晕图
warpimage	将用户提供的图像投影到地图上

在地图上画数据

函数	功能
contour/contourf	绘制等高线/填充等高线
imshow	绘制一个图像
pcolor/pcolormesh	绘制带规则/不规则网格的伪彩图
plot	绘制线条、标签
scatter	绘制带标签的点
quiver	绘制箭头
barbs	绘制风羽
drawgreatcircle	绘制大圆圈

Seaborn

1、频次直方图、KDE和密度图
使用KDE获取变量分布的平滑估计，并让频次直方图和KDE结合

import seaborn as sns
data=np.random.multivariate_normal([0,0],[[5,2],[2,2]],size=2000)
data=pd.DataFrame(data,columns=['x','y'])
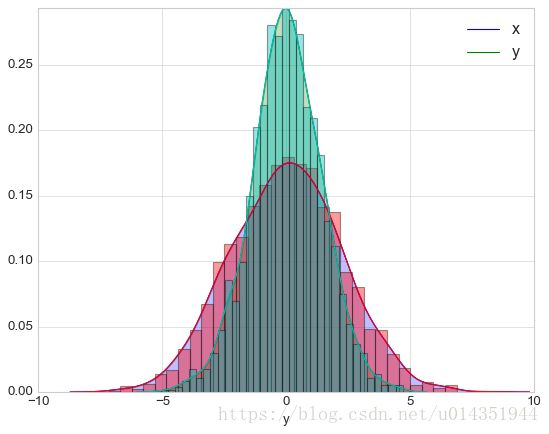
for col in 'xy':
    sns.kdeplot(data[col],shade=True)
sns.distplot(data['x'])
sns.distplot(data['y'])

如果输入的是二位数据集，那么就获得一个二位数据可视化图

sns.kdeplot(data)

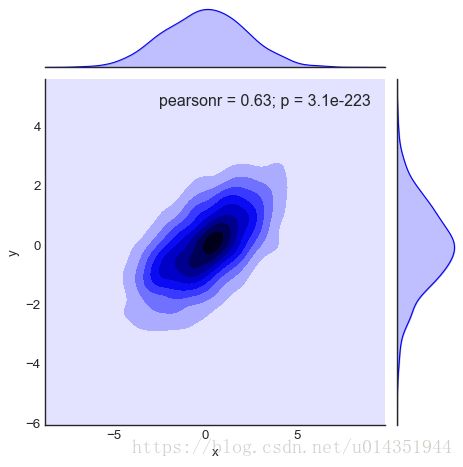
用sns.jointplot可以同时看到两个变量的联合分布与单变量的独立分布

with sns.axes_style('white'):
    sns.jointplot('x','y',data=data,kind='kde')

2、矩阵图

#载入鸢尾花数据集
iris=sns.load_dataset('iris')
iris.head()
输出：
sepal_length    sepal_width     petal_length    petal_width     species
0   5.1     3.5     1.4     0.2     setosa
1   4.9     3.0     1.4     0.2     setosa
2   4.7     3.2     1.3     0.2     setosa
3   4.6     3.1     1.5     0.2     setosa
4   5.0     3.6     1.4     0.2     setosa

sns.pairplot(iris,hue='species',size=2.5)

3、分面频次直方图

tips=sns.load_dataset('tips')
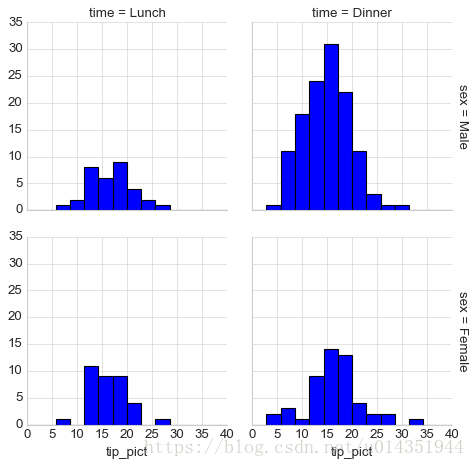
tips['tip_pict']=100*tips['tip']/tips['total_bill']
grid=sns.FacetGrid(tips,row='sex',col='time',margin_titles=True)
grid.map(plt.hist,'tip_pict',bins=np.linspace(0,40,15));

4、因子图

with sns.axes_style(style='ticks'):
    g=sns.factorplot('day','total_bill','sex',data=tips,kind='box')
    g.set_axis_labels('day','toatal bill')

5、联合分布

with sns.axes_style(style='white'):
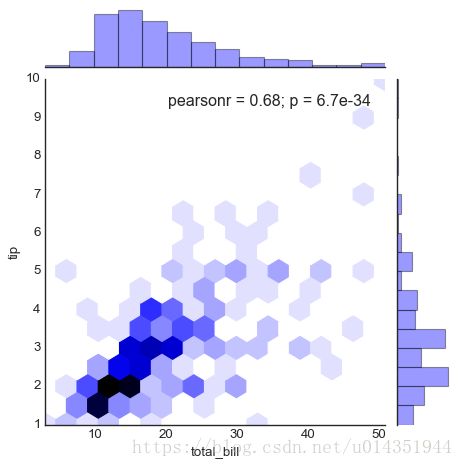
    sns.jointplot('total_bill','tip',data=tips,kind='hex')

6、条形图

planets=sns.load_dataset('planets')
with sns.axes_style('white'):
    g=sns.factorplot('year',data=planets,aspect=4.0,kind='count',hue='method',order=range(2001,2015))