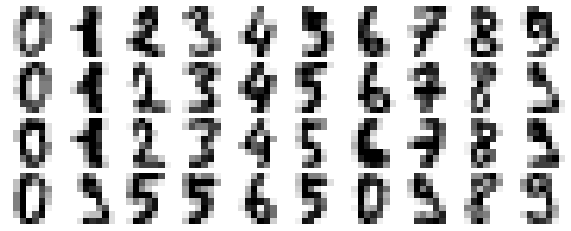Python数据科学手册-第5章机器学习
文章目录
- 机器学习的分类
- Scikit-Learn
- Scikit-Learn的数据表示
- Scikit-Learn的评估器API
- 应用:手写数字探索
- 超参数与模型验证
- 模型验证
- 选择最优模型
- 学习曲线
- 验证实践:网格搜索
- 特征工程
- 分类特征
- 文本特征
- 图像特征
- 衍生特征
- 缺失值填充
- 特征管道
- 专题:朴素贝叶斯分类
- 贝叶斯分类
- 高斯朴素贝叶斯
- 多项式朴素贝叶斯
- 朴素贝叶斯的应用场景
- 专题:线性回归
- 简单线性回归
- 基函数回归
- 正则化
- 案例:预测自行车流量
- 专题:支持向量机
- 支持向量机的由来
- 支持向量机:边界最大化
- 案例:人脸识别
- 专题:决策树与随机森林
- 随机森林的诱因:决策树
- 评估器集成算法:随机森林
- 随机森林回归
- 案例:用随机森林识别手写数字
- 专题:主成成分分析
- 用PCA作噪音过滤
- 案例:特征脸
- 专题:流形学习
- 流形学习:“HELLO”
- 多维标度法(MDS)
- 将MDS用于流行学习
- 非线性嵌入:当MDS失败时
- 非线性流形:局部线性嵌入
- 关于流形方法的一些思考
- 示例:用Isomap处理人脸数据
- 示例:手写数字的可视化结构
- 专题:K-means聚类
- K-means简介
- K-means算法:期望最大化
- 案例
- 专题:高斯混合模型
- k-means算法的缺陷
- 一般化E-M:高斯混合模型
- 将GMM用作密度估计
- 示例:用GMM生成新的数据
- 专题:核密度估计
- KDE的由来:直方图
- 核密度估计的实际应用
- 示例:球形空间的KDE
- 示例:不是很朴素的贝叶斯
- 应用:人脸识别管道
- HOG特征
- HOG实战:简单人脸识别器
- 注意事项与改进方案
机器学习的分类
- 有监督学习是指对数据的若干特征和若干标签之间的关联性进行建模的过程;只要模型被确定,就可以应用到新的未知数据上。可以分为分类与回归,分类的标签时离散值,回归的标签时连续值。
- 无监督学习是指对不带任何标签的数据特征进行建模,通常被看成是一种“让数据自己介绍自己”的过程。包括聚类和降维,聚类算法可以将数据分成不同的组别,而降维算法追求用更简洁的方式表示数据
- 还有一种半监督学习方法,介于有监督学习和无监督学习之间,半监督学习通常可以在数据标签不完整是使用
Scikit-Learn
Scikit-Learn的数据表示
- 数据表
基本的数据表就是二维网格数据,其中每一行表示数据集中的每个样本,而列表示构成每个样本的相关特征 - 特征矩阵
这个表格布局通过二维数组或矩阵的形式将信息清晰的表示出来,所以我们通常把这类矩阵称为特征矩阵 - 目标数组
目标数组一般是一位数组,其长度就是样本总数,通常都用一维的NumPy数组或Pandas的Series表示,目标数组可以是连续的数值类型,也可以是离散的类型
Scikit-Learn的评估器API
- API基础
Scikit-Learn的评估器API常用步骤:
(1) 通过从Scikit-Learn中导入适当的评估器类,选择模型类
(2) 用合适的数值对模型进行实例化,配置模型超参数
(3) 整理数据
(4) 调用模型实例的fit()方法对数据进行拟合
(5) 对新数据应用模型:
- 在有监督学习模型中,通常使用predict()方法预测数据的标签
- 在无监督学习模型中,通常使用transform()或predict()方法转换或推断数据的性质
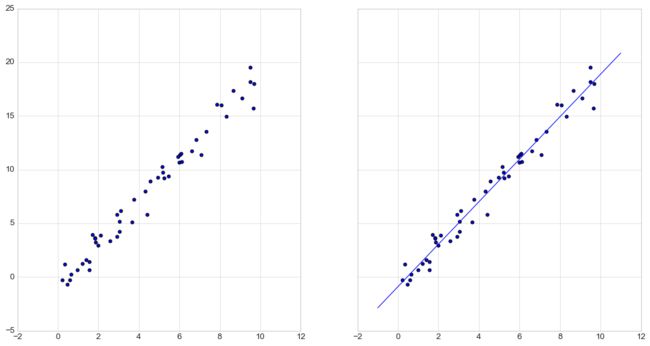
- 有监督学习实例:简单线性回归
import matplotlib.pyplot as plt
import numpy as np
plt.style.use('seaborn-whitegrid')
fig,ax=plt.subplots(1,2,sharex='col',sharey='row',figsize=(16,8))
rng=np.random.RandomState(42)
x=10*rng.rand(50)
y=2*x-1+rng.randn(50)
ax[0].scatter(x,y)
#选取模型类
from sklearn.linear_model import LinearRegression
#选取模型超参数,fit_intercept=True设置是否想要拟合直线的截距
model=LinearRegression(fit_intercept=True)
#将数据整理成特征矩阵和目标数组,这里需要将数据x整理成[n_samples,n_features]的形式
X=x[:,np.newaxis]
#用模型拟合数据
model.fit(X,y)
#所有通过fit方法获得的模型参数都带一条下划线,下面两个参数分别对直线的斜率和截距
display(model.coef_)
display(model.intercept_)
#预测新的数据
xfit=np.linspace(-1,11)
Xfit=xfit[:,np.newaxis]
yfit=model.predict(Xfit)
ax[1].scatter(x,y)
ax[1].plot(xfit,yfit)
#导入数据,构造数据集
import seaborn as sns
iris=sns.load_dataset('iris')
X_iris=iris.drop('species',axis=1)
y_iris=iris['species']
#将数据划分为训练集和测试集
from sklearn.cross_validation import train_test_split
Xtrain,Xtest,ytrain,ytest=train_test_split(X_iris,y_iris,random_state=1)
#导入高斯朴素贝叶斯方法
from sklearn.naive_bayes import GaussianNB
model=GaussianNB()
model.fit(Xtrain,ytrain)
y_model=model.predict(Xtest)
#用accuracy_score工具验证模型预测结果的准确性
from sklearn.metrics import accuracy_score
accuracy_score(ytest,y_model)
输出:0.9736842105263158
4. 无监督学习示例:鸢尾花数据降维
#选择模型
from sklearn.decomposition import PCA
#设置超参数
model=PCA(n_components=2)
#拟合数据
model.fit(X_iris)
#将数据转换为二维
X_2D=model.transform(X_iris)
iris['PCA1']=X_2D[:,0]
iris['PCA2']=X_2D[:,1]
sns.lmplot("PCA1","PCA2",hue='species',data=iris,fit_reg=False,palette="Blues_d")
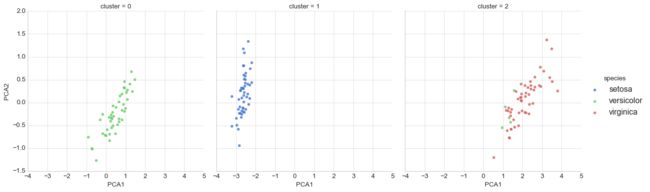
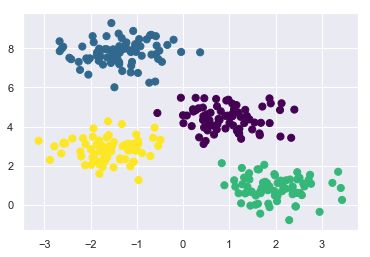
5. 无监督学习示例:鸢尾花数据聚类
#选择高斯混合模型
from sklearn.mixture import GMM
model=GMM(n_components=3,covariance_type='full')
model.fit(X_iris)
y_gmm=model.predict(X_iris)
iris['cluster']=y_gmm
sns.lmplot("PCA1","PCA2",data=iris,hue='species',col='cluster',fit_reg=False,palette="muted");
应用:手写数字探索
(1) 使用sklearn中接口加载数据并显示
from sklearn.datasets import load_digits
digits=load_digits()
import matplotlib.pyplot as plt
fig,axes=plt.subplots(10,10,figsize=(8,8),subplot_kw={'xticks':[],'yticks':[]},gridspec_kw=dict(hspace=0.1,wspace=0.1))
for i,ax in enumerate(axes.flat):
ax.imshow(digits.images[i],cmap='binary',interpolation='nearest')
ax.text(0.05,0.05,str(digits.target[i]),color='green',transform=ax.transAxes)

(2) 每个数字的分辨率是8*8所以每个样本有64个特征,可视化很困难,所以要使用无监督学习的方法将维度降到二维,这里使用的流形学习算法中的Isomap算法进行降维
from sklearn.manifold import Isomap
iso=Isomap(n_components=2)
iso.fit(digits.data)
data_projected=iso.transform(digits.data)
plt.scatter(data_projected[:,0],data_projected[:,1],c=digits.target,edgecolors='none',alpha=0.5,cmap=plt.cm.get_cmap('Spectral',10))
plt.colorbar(label='digit label',ticks=range(10))
plt.clim(-0.5,9.5);

(3) 详见数据分为训练集和测试集,然后用高斯贝叶斯模型来拟合
Xtrain,Xtest,ytrain,ytest=train_test_split(digits.data,digits.target,random_state=0)
model=GaussianNB()
model.fit(Xtrain,ytrain)
y_model=model.predict(Xtest)
accuracy_score(ytest,y_model)
输出:0.8333333333333334
这是就可以使用混淆矩阵进行分析模型在哪里表现不好,混淆矩阵可以通过sklearn计算
from sklearn.metrics import confusion_matrix
mat=confusion_matrix(ytest,y_model)
sns.heatmap(mat,square=True,annot=True,cbar=False)
plt.xlabel('predicted value')
plt.ylabel('true value');
也可以将错误的样本显示出来,如绿色表示正确,蓝色表示错误
fig,axes=plt.subplots(10,10,figsize=(8,8),subplot_kw={'xticks':[],'yticks':[]},gridspec_kw=dict(hspace=0.1,wspace=0.1))
test_images=Xtest.reshape(-1,8,8)
for i,ax in enumerate(axes.flat):
ax.imshow(test_images[i],cmap='binary',interpolation='nearest')
ax.text(0.05,0.05,str(y_model[i]),color='green' if (ytest[i]==y_model[i]) else 'blue',transform=ax.transAxes)
超参数与模型验证
模型验证
- 错误的模型验证方法
使用同一数据训练和评估模型,在理想情况准确率很高,但这并不能说明模型对新的数据的拟合程度
from sklearn.datasets import load_iris
iris=load_iris()
x=iris.data
y=iris.target
from sklearn.neighbors import KNeighborsClassifier
mode=KNeighborsClassifier(n_neighbors=1)
model.fit(x,y)
y_model=model.predict(x)
accuracy_score(y,y_model)
输出:0.96
2. 模型验证正确方法:留出集
将数据集留出一部分作为验证集,使用验证集来检验模型性能
x1,x2,y1,y2=train_test_split(x,y,random_state=0,train_size=0.5)
model.fit(x1,y1)
y2_model=model.predict(x2)
accuracy_score(y2,y2_model)
输出:0.9466666666666667
3. 交叉验证
使用留出集有一个缺点,就是模型失去了一部分训练机会,尤其是在训练数据集规模比较小的时候,所以就让数据的每个子集既是训练集,又是训练集

y2_model=model.fit(x1,y1).predict(x2)
y1_model=model.fit(x2,y2).predict(x1)
accuracy_score(y1,y1_model),accuracy_score(y2,y2_model)
输出:(0.9733333333333334, 0.9466666666666667)
将数据集分成两个子集叫作两轮交叉验证,也可以扩展这个概念,例如五轮交叉验证
from sklearn.cross_validation import cross_val_score
cross_val_score(model,x,y,cv=5)
输出:array([0.93333333, 0.96666667, 0.93333333, 0.93333333, 1. ])
还有一些其他的交叉验证方法如LOO交叉验证,每次只保留一个样本做测试
from sklearn.cross_validation import LeaveOneOut
cross_val_score(model,x,y,cv=LeaveOneOut(len(x)))
输出:
array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
1., 0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
1., 1., 0., 1., 1., 1., 1., 1., 1., 0., 1., 1., 1., 1., 1., 1., 1.,
1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
1., 1., 1., 1., 0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 0., 0., 1.,
1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
这时计算所有实验准确率的均值就可以得到模型的预测准确性了
选择最优模型
- 偏差和方差的平衡
上面左图这样的模型被认为欠拟合,它希望找一条直线去拟合数据,但是数据本质上比直线要复杂,这样的模型也叫作高偏差
上面右图这样的模型被认为过拟合,它十分准确的描述了训练数据,当过多的学习了数据的噪音,这样的模型也叫作高方差
通过计算不同模型复杂度(例如多项式的次数)下的训练分数和验证分数来找到最好的模型 - Scikit-Learn验证曲线
# 构造数据
import numpy as np
def make_data(N=30, err=0.8, rseed=1):
# randomly sample the data
rng = np.random.RandomState(rseed)
X = rng.rand(N, 1) ** 2
y = 10 - 1. / (X.ravel() + 0.1)
if err > 0:
y += err * rng.randn(N)
return X, y
# 构建带多项式预处理器的简单线性回归模型
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
def PolynomialRegression(degree=2, **kwargs):
return make_pipeline(PolynomialFeatures(degree),
LinearRegression(**kwargs));
# 将不同次数的多项式拟合曲线画出来
X, y = make_data()
xfit = np.linspace(-0.1, 1.0, 1000)[:, None]
model1 = PolynomialRegression(1).fit(X, y)
model20 = PolynomialRegression(20).fit(X, y)
fig, ax = plt.subplots(1, 2, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)
ax[0].scatter(X.ravel(), y, s=40)
ax[0].plot(xfit.ravel(), model1.predict(xfit), color='gray')
ax[0].axis([-0.1, 1.0, -2, 14])
ax[0].set_title('High-bias model: Underfits the data', size=14)
ax[1].scatter(X.ravel(), y, s=40)
ax[1].plot(xfit.ravel(), model20.predict(xfit), color='gray')
ax[1].axis([-0.1, 1.0, -2, 14])
ax[1].set_title('High-variance model: Overfits the data', size=14)
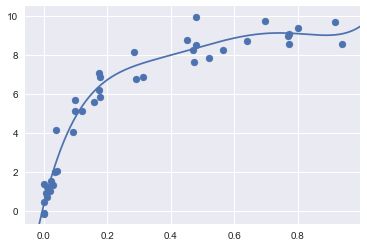
在这个例子中模型复杂性的关键就是多项式的次数,想要知道最好的次数去平衡偏差和方差就需要绘制验证曲线,则可以使用sklearn中validation_curve函数实现
from sklearn.learning_curve import validation_curve
degree=np.arange(0,21)
train_score,val_score=validation_curve(PolynomialRegression(),X,y,'polynomialfeatures__degree',degree,cv=7)
plt.plot(degree,np.median(train_score,1),color='blue',label='training score')
plt.plot(degree,np.median(val_score,1),color='red',label='validation score')
plt.legend(loc='best')
plt.ylim(0,1)
plt.xlabel('degree')
plt.ylabel('score');
由验证曲线可以看出最好的是三次多项式
学习曲线
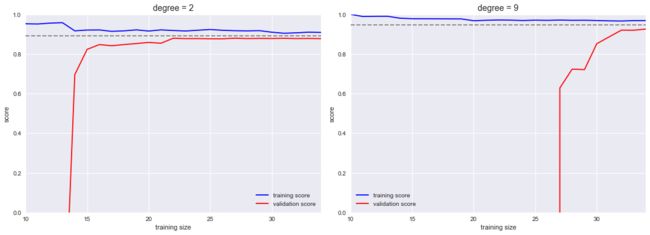
影响模型复杂度的另一个重要因素是最优模型一般是收到训练数据量的影响的,反应训练集规模的训练得分/验证得分曲线被称为学习曲线。
学习曲线的重要特征就是,随着训练样本数量的增加,分数会会收敛到定值,此时增加更多的训练样本也无济于事
使用sklearn绘制学习曲线
from sklearn.learning_curve import learning_curve
fig,ax=plt.subplots(1,2,figsize=(16,6))
fig.subplots_adjust(left=0.0625,right=0.95,wspace=0.1)
for i,degree in enumerate([2,9]):
N,train_lc,val_lc = learning_curve(PolynomialRegression(degree),X,y,cv=7,train_sizes=np.linspace(0.3,1,25))
ax[i].plot(N,np.mean(train_lc,1),color='blue',label='training score')
ax[i].plot(N,np.mean(val_lc,1),color='red',label='validation score')
ax[i].hlines(np.mean([train_lc[-1],val_lc[-1]]),N[0],N[-1],color='gray',linestyle='dashed')
ax[i].set_ylim(0, 1)
ax[i].set_xlim(N[0], N[-1])
ax[i].set_xlabel('training size')
ax[i].set_ylabel('score')
ax[i].set_title('degree = {0}'.format(degree), size=14)
ax[i].legend(loc='best')
验证实践:网格搜索
在实际工作中,模型通常会有多个得分转折点,因此验证曲线和学习曲线的图形会从二位曲线变成多维曲面,这种高维可视化很难展现,因此从图中找到验证得分的最大值不容易。Scikit-Learn在grid_search提供了自动化工具解决这个问题。
使用Scikit-Learn的GridSearchCV元评估器来设置这些参数
from sklearn.grid_search import GridSearchCV
param_grid={'polynomialfeatures__degree': np.arange(21),
'linearregression__fit_intercept':[True,False],
'linearregression__normalize':[True,False]
}
grid=GridSearchCV(PolynomialRegression(),param_grid,cv=7)
grid.fit(X,y)
grid.best_params_
输出:
{‘linearregression__fit_intercept’: True,
‘linearregression__normalize’: False,
‘polynomialfeatures__degree’: 5}
使用最优参数拟合数据
model=grid.best_estimator_
plt.scatter(X.ravel(),y)
lim=plt.axis()
y_test=model.fit(X,y).predict(X_test)
plt.plot(X_test.ravel(),y_test)
plt.axis(lim);
特征工程
找出与问题相关的任何信息,把他们转换成特征矩阵的数值
分类特征
浏览房屋数据是除了房价、面积之类的数值特征,还会有“地点”等信息,如
data = [
{'price': 850000, 'rooms': 4, 'neighborhood': 'Queen Anne'},
{'price': 700000, 'rooms': 3, 'neighborhood': 'Fremont'},
{'price': 650000, 'rooms': 3, 'neighborhood': 'Wallingford'},
{'price': 600000, 'rooms': 2, 'neighborhood': 'Fremont'}
]
面对这种情况,常用的解决方法是独热编码。将neighborhood字段转换成三列来表示三个地点的标签
from sklearn.feature_extraction import DictVectorizer
vec=DictVectorizer(sparse=False,dtype=int)
vec.fit_transform(data)
输出:
array([[ 0, 1, 0, 850000, 4],
[ 1, 0, 0, 700000, 3],
[ 0, 0, 1, 650000, 3],
[ 1, 0, 0, 600000, 2]], dtype=int32)
#查看特征名称
vec.get_feature_names()
输出:
[‘neighborhood=Fremont’,
‘neighborhood=Queen Anne’,
‘neighborhood=Wallingford’,
‘price’,
‘rooms’]
但这种方法有一个缺点就是,数据的维数急剧的增加,由于被编码的数据有许多0,所以可以用稀疏矩阵表示
vec=DictVectorizer(sparse=True,dtype=int)
vec.fit_transform(data)
文本特征
文本数据采集最简单的编码方法之一就是单词统计
from sklearn.feature_extraction.text import CountVectorizer
sample = ['problem of evil',
'evil queen',
'horizon problem']
vec=CountVectorizer()
X=vec.fit_transform(sample)
import pandas as pd
pd.DataFrame(X.toarray(),columns=vec.get_feature_names())
Out:
evil horizon of problem queen
0 1 0 1 1 0
1 1 0 0 0 1
2 0 1 0 1 0
但是这样一些常用词就会聚集太高的权重,解决这一问题就是通过TF-IDF,通过单词在文档中出现的频率来衡量其权重
from sklearn.feature_extraction.text import TfidfVectorizer
vec=TfidfVectorizer()
X=vec.fit_transform(sample)
pd.DataFrame(X.toarray(),columns=vec.get_feature_names())
Out:
evil horizon of problem queen
0 0.517856 0.000000 0.680919 0.517856 0.000000
1 0.605349 0.000000 0.000000 0.000000 0.795961
2 0.000000 0.795961 0.000000 0.605349 0.000000
图像特征
最简单的图像编码方法:用像素表示图像
衍生特征
我们在将一个线性回归转换为多项式回归时,并不是通过改变模型来实现的而是通过改变输入数据,这种处理方式有时被称为基函数回归
x = np.array([1, 2, 3, 4, 5])
y = np.array([4, 2, 1, 3, 7])
X=x[:,np.newaxis]
from sklearn.preprocessing import PolynomialFeatures
poly=PolynomialFeatures(degree=3,include_bias=False)
X2=poly.fit_transform(X)
X2
Out:
array([[ 1., 1., 1.],
[ 2., 4., 8.],
[ 3., 9., 27.],
[ 4., 16., 64.],
[ 5., 25., 125.]])
缺失值填充
这里使用的列均值替换缺失值
from numpy import nan
X = np.array([[ nan, 0, 3 ],
[ 3, 7, 9 ],
[ 3, 5, 2 ],
[ 4, nan, 6 ],
[ 8, 8, 1 ]])
y = np.array([14, 16, -1, 8, -5])
from sklearn.preprocessing import Imputer
imp=Imputer(strategy='mean')
X2=imp.fit_transform(X)
X2
Out:
array([[4.5, 0. , 3. ],
[3. , 7. , 9. ],
[3. , 5. , 2. ],
[4. , 5. , 6. ],
[8. , 8. , 1. ]])
特征管道
当需要将多个步骤穿起来的时候可以使用make_pipeline
from sklearn.pipeline import make_pipeline
model=make_pipeline(Imputer(strategy='mean'),
PolynomialFeatures(degree=2),
LinearRegression()
)
专题:朴素贝叶斯分类
贝叶斯分类
贝叶斯公式:计算具有某些特征的样本属于某类标签的概率
P ( L ∣ f e a t u r e s ) = P ( f e a t u r e s ∣ L ) P ( L ) P ( f e a t u r e s ) P(L~|~{\rm features}) = \frac{P({\rm features}~|~L)P(L)}{P({\rm features})} P(L ∣ features)=P(features)P(features ∣ L)P(L)
高斯朴素贝叶斯
构造服从高斯分布的数据
from sklearn.datasets import make_blobs
X,y=make_blobs(100,2,centers=2,random_state=2,cluster_std=1.5)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap='RdBu')
高斯朴素贝叶斯在sklearn中的实现
from sklearn.naive_bayes import GaussianNB
model=GaussianNB()
model.fit(X,y)
rng=np.random.RandomState(0)
Xnew=[-6,-14]+[14,18]*rng.rand(2000,2)
ynew=model.predict(Xnew)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap='RdBu')
lim=plt.axis()
plt.scatter(Xnew[:,0],Xnew[:,1],c=ynew,s=20,cmap='RdBu',alpha=0.6)
plt.axis(lim);
在分类记过中可以看到一个弯曲的边界,高斯朴素贝叶斯的边界是二次方曲线
可以使用predict_proba方法计算样本属于摸个标签的概率
yprob=model.predict_proba(Xnew)
yprob[-8:].round(2)
Out:
array([[0.89, 0.11],
[1. , 0. ],
[1. , 0. ],
[1. , 0. ],
[1. , 0. ],
[1. , 0. ],
[0. , 1. ],
[0.15, 0.85]])
多项式朴素贝叶斯
多项式朴素贝叶斯的假设特征是由一个简单度显示分布生成的,多项分布可以描述各种类型样本出现次数的概率,因此多项式朴素贝叶斯非常实用用于描述出现次数或者出现次数比例的特征
- 案例:文本分类
获取20个网络新闻组语料库中的数据,这里选取四类新闻下载训练集和测试集
from sklearn.datasets import fetch_20newsgroups
data=fetch_20newsgroups()
categories=['talk.religion.misc','soc.religion.christian','sci.space','comp.graphics']
train=fetch_20newsgroups(subset='train',categories=categories)
test=fetch_20newsgroups(subset='test',categories=categories)
train.data[5]
Out:
"From: dmcgee@uluhe.soest.hawaii.edu (Don McGee)
Subject: Federal Hearing
Originator: dmcgee@uluhe
Organization: School of Ocean and Earth Science and Technology
Distribution: usa
Lines: 10
Fact or rumor....? Madalyn Murray O'Hare an atheist who eliminated the
use of the bible reading and prayer in public schools 15 years ago is now
going to appear before the FCC with a petition to stop the reading of the
Gospel on the airways of America. And she is also campaigning to remove
Christmas programs, songs, etc from the public schools. If it is true
then mail to Federal Communications Commission 1919 H Street Washington DC
20054 expressing your opposition to her request. Reference Petition number
2493.
构造管道间TF-IDF和多项式朴素贝叶斯分类器组合在一起
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.pipeline import make_pipeline
model = make_pipeline(TfidfVectorizer(),MultinomialNB())
将模型应用到训练数据上,预测出每个测试数据的标签
model.fit(train.data,train.target)
labels=model.predict(test.data)
使用混淆矩阵统计测试数据的真实标签与预测标签的结果
from sklearn.metrics import confusion_matrix
mat=confusion_matrix(test.target,labels)
sns.heatmap(mat.T,square=True,annot=True,fmt='d',cbar=False,
xticklabels=train.target_names,yticklabels=train.target_names)
plt.xlabel('true label')
plt.ylabel('predicted label');
朴素贝叶斯的应用场景
由于朴素贝叶斯对数据有严格的假设,因此它的训练效果通常比复杂模型的差
优点:
- 训练和预测的速度非常快
- 直接使用概率预测
- 通常很容易解释
- 可调参数非常少
朴素贝叶斯分类器非常适合用于以下应用场景:
- 假设分布函数与数据匹配
- 各种类型的区分度很高,模型复杂度不重要
- 非常高维度的数据,模型复杂度不重要
专题:线性回归
简单线性回归
拟合直线模型y=ax+b
rng=np.random.RandomState(1)
x=10*rng.rand(50)
y=2*x-5+rng.randn(50)
from sklearn.linear_model import LinearRegression
model=LinearRegression(fit_intercept=True)
model.fit(x[:,np.newaxis],y)
xfit=np.linspace(0,10,1000)
yfit=model.predict(xfit[:,np.newaxis])
plt.scatter(x,y)
plt.plot(xfit,yfit);
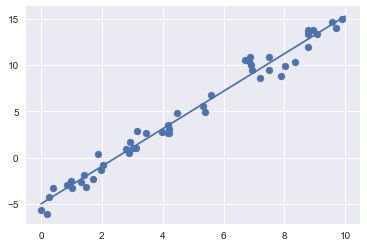
LinearRegression还可以拟合多维度的线性回归模型: y = a 0 + a 1 x 1 + a 2 x 2 + . . . y=a_0+a_1x_1+a_2x_2+... y=a0+a1x1+a2x2+...
rng=np.random.RandomState(1)
X=10*rng.rand(100,3)
y=0.5+np.dot(X,[1.5,-2.,1.])
model.fit(X,y)
print(model.intercept_)
print(model.coef_)
Out:
0.5000000000000144
[ 1.5 -2. 1. ]
基函数回归
可以通过基函数对原始数据进行转换,从而将变量间的线性回归模型转换为非线性回归模型如PolynomialRegression就是将模型变成多项式回归,变成: y = a 0 + a 2 x 2 + a 3 x 3 + . . . y=a_0+a_2x^2+a_3x^3+... y=a0+a2x2+a3x3+...
- 多项式基函数
使用7次多项式回归拟合带噪的正弦波
from sklearn.pipeline import make_pipeline
poly_model=make_pipeline(PolynomialFeatures(7),LinearRegression())
rng=np.random.RandomState(1)
x = 10 * rng.rand(50)
y = np.sin(x) + 0.1 * rng.randn(50)
poly_model.fit(x[:,np.newaxis], y)
yfit=poly_model.predict(xfit[:,np.newaxis])
plt.scatter(x,y)
plt.plot(xfit,yfit);
2. 高斯基函数
自定义转换器
from sklearn.base import BaseEstimator,TransformerMixin
class GaussianFeatures(BaseEstimator,TransformerMixin):
def __init__(self,N,width_factor=2.0):
self.N=N
self.width_factor=width_factor
@staticmethod
def _gauss_basis(x,y,width,axis=None):
arg=(x-y)/width
return np.exp(-0.5*np.sum(arg**2,axis))
def fit(self,X,y=None):
#在数据区间中创建N个高斯分布中心
self.centers_=np.linspace(X.min(),X.max(),self.N)
self.width_=self.width_factor*(self.centers_[1]-self.centers_[0])
return self
def transform(self,X):
return self._gauss_basis(X[:,:,np.newaxis],self.centers_,self.width_,axis=1)
gauss_model=make_pipeline(GaussianFeatures(20),LinearRegression())
gauss_model.fit(x[:,np.newaxis],y)
yfit=gauss_model.predict(xfit[:,np.newaxis])
plt.scatter(x,y)
plt.plot(xfit,yfit)
plt.xlim(0,10);
正则化
def basis_plot(model, title=None):
fig, ax = plt.subplots(2, figsize=(16,6),sharex=True)
model.fit(x[:, np.newaxis], y)
ax[0].scatter(x, y)
ax[0].plot(xfit, model.predict(xfit[:, np.newaxis]))
ax[0].set(xlabel='x', ylabel='y', ylim=(-1.5, 1.5))
if title:
ax[0].set_title(title)
ax[1].plot(model.steps[0][1].centers_,
model.steps[1][1].coef_)
ax[1].set(xlabel='basis location',
ylabel='coefficient',
xlim=(0, 10))
model = make_pipeline(GaussianFeatures(30), LinearRegression())
basis_plot(model)
下面的图显示了每个位置上基函数的振幅,当基函数重叠的时候,通常就表明出现了过拟合,需要对较大的模型参数进行惩罚,从而抑制模型剧烈波动,这个惩罚的机制被称为正则化。
- 岭回归(L2范数正则化)
其处理方法是对模型系数平方和(L2范数)进行惩罚, α \alpha α是一个只有参数,用来控制惩罚的力度
P = α ∑ n = 1 N θ n 2 P = \alpha\sum_{n=1}^N \theta_n^2 P=αn=1∑Nθn2
from sklearn.linear_model import Ridge
model=make_pipeline(GaussianFeatures(30),Ridge(alpha=0.1))
basis_plot(model,title='Ridge Regression')
岭回归的一个重要优点是,它可以非常高效的计算,几乎没有小号更多的计算资源
2. Lasso正则化(L1范数)
对模型系数绝对值的和进行惩罚,它虽然在形式上接近岭回归,但结果与岭回归差别很大,如,因其几何特性,Lasso正则化倾向于构建稀疏模型,也就是说,它更喜欢建模型稀疏设置为0
具体解释参考:http://freemind.pluskid.org/machine-learning/sparsity-and-some-basics-of-l1-regularization/#ed61992b37932e208ae114be75e42a3e6dc34cb3
from sklearn.linear_model import Lasso
model=make_pipeline(GaussianFeatures(30),Lasso(alpha=0.01))
basis_plot(model,title='Lasso Regression')
案例:预测自行车流量
#加载数据集,用日期作为索引
import pandas as pd
counts=pd.read_csv('Fremont_Bridge_Hourly_Bicycle_Counts_by_Month_October_2012_to_present.csv',index_col='Date',parse_dates=True)
weather=pd.read_csv('BicycleWeather.csv',index_col='DATE',parse_dates=True)
#计算每一天的自行车流量,并加入7列0~1表示星期几
daily=counts.resample('d').sum()
daily['Total']=daily.sum(axis=1)
daily=daily[['Total']]
days = ['Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat', 'Sun']
for i in range(7):
daily[days[i]]=(daily.index.dayofweek==i).astype(float)
#骑车的人数在节假日也有所变换,因此,再增加一列表示当天时候为节假日
from pandas.tseries.holiday import USFederalHolidayCalendar
cal=USFederalHolidayCalendar()
holidays=cal.holidays('2012','2016')
daily=daily.join(pd.Series(1,index=holidays,name='holiday'))
daily['holiday'].fillna(0,inplace=True)
#白昼时间也可能会影响骑车人数
def hours_of_daylight(date,axis=23.44,latitude=47.61):
#计算指定日期的白昼时间
days=(date-pd.datetime(2000,12,21)).days
m = (1. - np.tan(np.radians(latitude))
* np.tan(np.radians(axis) * np.cos(days * 2 * np.pi / 365.25)))
return 24.*np.degrees(np.arccos(1-np.clip(m,0,2)))/180.
daily['daylight_hrs']=list(map(hours_of_daylight,daily.index))
# 温度是按照1/10摄氏度统计的,首先转换为摄氏度
weather['TMIN']/=10
weather['TMAX']/=10
weather['Temp(C)']=0.5*(weather['TMIN']+weather['TMAX'])
# 降雨量也是按照1/10mm统计的,转换为英寸
weather['PRCP']/=254
weather['dry day']=(weather['PRCP']==0).astype(int)
daily=daily.join(weather[['PRCP','Temp(C)','dry day']])
#增加一个从1开始递增的计数器,表示一年已经过去了多少天
daily['annual']=(daily.index-daily.index[0]).days/365.
daily.head()
Out:
Total Mon Tue Wed Thu Fri Sat Sun holiday daylight_hrs PRCP Temp(C) dry day annual
Date
2012-10-03 3521.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 0.0 11.277359 0.0 13.35 1.0 0.000000
2012-10-04 3475.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 11.219142 0.0 13.60 1.0 0.002740
2012-10-05 3148.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 11.161038 0.0 15.30 1.0 0.005479
2012-10-06 2006.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 11.103056 0.0 15.85 1.0 0.008219
2012-10-07 2142.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0 11.045208 0.0 15.85 1.0 0.010959
对数据建立线性回归模型
daily.dropna(axis=0,how='any',inplace=True)
column_names = ['Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat', 'Sun', 'holiday',
'daylight_hrs', 'PRCP', 'dry day', 'Temp(C)', 'annual']
X=daily[column_names]
y=daily['Total']
#这里设不设置截距都行,因为每一天的总流量
model=LinearRegression(fit_intercept=True)
model.fit(X,y)
daily['predicted']=model.predict(X)
#预测结果
daily[['Total','predicted']].plot(alpha=0.5)
使用自举重采样方法快速计算数据的不确定性
可以看出星期特征比较稳定,工作日骑车的人数显然比周末和节假日多,白昼时间没增加一个小时,就平均增加129±9个骑车的人
params=pd.Series(model.coef_,index=X.columns)
from sklearn.utils import resample
np.random.seed(1)
err=np.std([model.fit(*resample(X,y)).coef_ for i in range(1000)],0)
print(pd.DataFrame({'effect':params.round(0),
'error':err.round(0)
}))
Out:
effect error
Mon 520.0 34.0
Tue 582.0 35.0
Wed 613.0 35.0
Thu 440.0 35.0
Fri 161.0 34.0
Sat -1112.0 33.0
Sun -1204.0 31.0
holiday -1241.0 163.0
daylight_hrs 126.0 9.0
PRCP -622.0 62.0
dry day 584.0 33.0
Temp(C) 65.0 4.0
annual 19.0 18.0
专题:支持向量机
支持向量机的由来
贝叶斯分类器(生成分类方法),是对每个类进行随机分布的假设,然后用生成的模型估计新数据点的标签
判别分类方法:使用一条分割线或者流形体将各种类型分割开
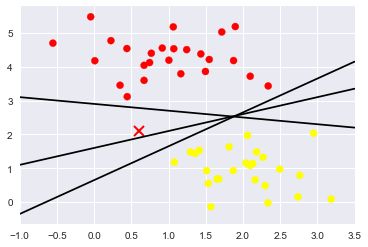
在我们尝试构造分类模型的时候,方向在两种类型之间有不知一条直线将他们完美分割
from sklearn.datasets.samples_generator import make_blobs
X, y = make_blobs(n_samples=50, centers=2,
random_state=0, cluster_std=0.60)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn');
xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plt.plot([0.6], [2.1], 'x', color='red', markeredgewidth=2, markersize=10)
for m, b in [(1, 0.65), (0.5, 1.6), (-0.2, 2.9)]:
plt.plot(xfit, m * xfit + b, '-k')
plt.xlim(-1, 3.5);
支持向量机:边界最大化
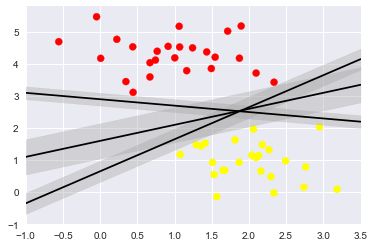
支持向量机:不再画一条细线来区分类型,而是画一条道最近点边界、有宽度的线条,选择边界最大的那条线是模型最优解
xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
for m, b, d in [(1, 0.65, 0.33), (0.5, 1.6, 0.55), (-0.2, 2.9, 0.2)]:
yfit = m * xfit + b
plt.plot(xfit, yfit, '-k')
plt.fill_between(xfit, yfit - d, yfit + d, edgecolor='none',
color='#AAAAAA', alpha=0.4)
plt.xlim(-1, 3.5);
- 拟合支持向量机
#使用线性核函数,并将C设置得很大
from sklearn.svm import SVC
model=SVC(kernel='linear',C=1E10)
model.fit(X,y)
#创建一个辅助函数画出SVM的局车边界
def plot_svc_decision_function(model,ax=None,plot_support=True):
#画二维SVC的决策函数
if ax is None:
ax=plt.gca()
xlim=ax.get_xlim()
ylim=ax.get_ylim()
#创建评估模型的网格
x=np.linspace(xlim[0],xlim[1],30)
y=np.linspace(ylim[0],ylim[1],30)
Y,X=np.meshgrid(y,x)
xy=np.vstack([X.ravel(),Y.ravel()]).T
P=model.decision_function(xy).reshape(X.shape)
#画决策边界和边界
ax.contour(X,Y,P,colors='k',levels=[-1,0,1],alpha=0.5,linestyles=['--','-','--'])
#画支持向量
if plot_support:
ax.scatter(model.support_vectors_[:,0],model.support_vectors_[:,1],s=300,linewidth=1,facecolors='none');
ax.set_xlim(xlim)
ax.set_ylim(ylim)
#绘制决策边界
plt.scatter(X[:,0],X[:,1],c =y,s=50,cmap='autumn')
plot_svc_decision_function(model=model)
支持向量的坐标存放在分类器的support_vectors_属性中
model.support_vectors_
Out:
array([[0.44359863, 3.11530945],
[2.33812285, 3.43116792],
[2.06156753, 1.96918596]])
对于远离边界的数据点不敏感的特点正是SVM的特点
def plot_svm(N=10,ax=None):
X,y=make_blobs(n_samples=N,centers=2,random_state=0,cluster_std=0.60)
X=X[:N]
y=y[:N]
model=SVC(kernel='linear',C=1E10)
model.fit(X,y)
ax=ax or plt.gca()
ax.scatter(X[:,0],X[:,1],c=y,s=50,cmap='autumn')
ax.set_xlim(-1,4)
ax.set_ylim(-1,6)
plot_svc_decision_function(model,ax)
fig,ax=plt.subplots(1,2,figsize=(16,6))
fig.subplots_adjust(left=0.0625,right=0.95,wspace=0.1)
for axi,N in zip(ax,[60,120]):
plot_svm(N,axi)
axi.set_title('N={0}'.format(N))
从下图可以看出,虽然训练样本的数量变化了,但是模型并没有改变
![]()
2. 超越线性边界:核函数SVM模型
将SVM模型和核函数组合使用,可以实现用线性分类器拟合非线性关系
from sklearn.datasets.samples_generator import make_circles
X, y = make_circles(100, factor=.1, noise=.1)
clf = SVC(kernel='linear').fit(X, y)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plot_svc_decision_function(clf, plot_support=False);
对于非线性可分的数据,线性分类器并不能进行分类
可以参考基函数回归的思想,将数据投影到高维空间,从而使线性分类器可以用,这里使用的是径向基函数、
r = np.exp(-(X ** 2).sum(1))
可视化新增加的维度
from mpl_toolkits import mplot3d
def plot_3D(elev=30, azim=30, X=X, y=y):
ax = plt.subplot(projection='3d')
ax.scatter3D(X[:, 0], X[:, 1], r, c=y, s=50, cmap='autumn')
ax.view_init(elev=elev, azim=azim)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('r')
interact(plot_3D, elev=[-45, 45], azip=(-180, 180),
X=fixed(X), y=fixed(y));
可以看到增加了新的维度后,数据变成了线性可分
只用将kernel设置为RBF就是使用的径向基函数
clf=SVC(kernel='rbf',C=1E6)
clf.fit(X,y)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap='autumn')
plot_svc_decision_function(clf)
plt.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1],s=300,lw=1,facecolors='none');
3. SVM优化:软化边界
当数据中有脏数据时,数据就会重叠,模型并不能很好的拟合数据
X,y=make_blobs(n_samples=100,centers=2,random_state=0,cluster_std=1.2)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap='autumn')
SVM中的C就是这个修正因子就是来决定点在边界线内的数量,C的数值越大,边界线内的数据点越少,C的数值越小,边界线内的数据点越多
X,y=make_blobs(n_samples=100,centers=2,random_state=0,cluster_std=0.8)
fig,ax=plt.subplots(1,2,figsize=(16,6))
fig.subplots_adjust(left=0.0625,right=0.95,wspace=0.1)
for axi,C in zip(ax,[10.0,0.1]):
model=SVC(kernel='linear',C=C).fit(X,y)
axi.scatter(X[:,0],X[:,1],c=y,s=50,cmap='autumn')
plot_svc_decision_function(model,axi)
axi.scatter(model.support_vectors_[:,0],model.support_vectors_[:,1],s=300,lw=1,facecolors='none')
axi.set_title('C={0:.1f}'.format(C),size=14)
案例:人脸识别
导入wild数据集中带标记的人脸图像,并显示部分图像
from sklearn.datasets import fetch_lfw_people
faces=fetch_lfw_people(min_faces_per_person=60)
fig,ax=plt.subplots(3,5)
for i,axi in enumerate(ax.flat):
axi.imshow(faces.images[i],cmap='bone')
axi.set(xticks=[],yticks=[],xlabel=faces.target_names[faces.target[i]])
from sklearn.svm import SVC
from sklearn.decomposition import PCA
from sklearn.pipeline import make_pipeline
pca=PCA(n_components=150,whiten=True,random_state=42,svd_solver='randomized')
svc=SVC(kernel='rbf',class_weight='balanced')
model=make_pipeline(pca,svc)
将数据集分解成训练集和测试集
使用网格搜索交叉验证来寻找最优参数组合
from sklearn.cross_validation import train_test_split
Xtrian,Xtest,ytrain,ytest=train_test_split(faces.data,faces.target,random_state=42)
from sklearn.grid_search import GridSearchCV
param_grid={'svc__C':[1,5,10,50],'svc__gamma':[0.0001,0.0005,0.001,0.005]}
grid=GridSearchCV(model,param_grid=param_grid)
%time grid.fit(Xtrian,ytrain)
print(grid.best_params_)
Out:
Wall time: 14.3 s
{'svc__C': 10, 'svc__gamma': 0.001}
对测试数据集进行预测,并将一些测试图片与预测图片进行对比
model=grid.best_estimator_
yfit=model.predict(Xtest)
fig,ax=plt.subplots(4,6)
for i,axi in enumerate(ax.flat):
axi.imshow(Xtest[i].reshape(62,47),cmap='bone')
axi.set(xticks=[],yticks=[])
axi.set_ylabel(faces.target_names[yfit[i]].split()[-1],color='black' if yfit[i] == ytest[i] else 'red')
fig.suptitle('Predicted Names; Incorrect Labels in Red', size=14);
from sklearn.metrics import classification_report
print(classification_report(ytest,yfit,target_names=faces.target_names))
Out:
precision recall f1-score support
Ariel Sharon 0.65 0.73 0.69 15
Colin Powell 0.80 0.87 0.83 68
Donald Rumsfeld 0.74 0.84 0.79 31
George W Bush 0.92 0.83 0.88 126
Gerhard Schroeder 0.86 0.83 0.84 23
Hugo Chavez 0.93 0.70 0.80 20
Junichiro Koizumi 0.92 1.00 0.96 12
Tony Blair 0.85 0.95 0.90 42
avg / total 0.86 0.85 0.85 337
绘制混淆矩阵
from sklearn.metrics import confusion_matrix
mat = confusion_matrix(ytest, yfit)
sns.heatmap(mat.T, square=True, annot=True, fmt='d', cbar=False,
xticklabels=faces.target_names,
yticklabels=faces.target_names)
plt.xlabel('true label')
plt.ylabel('predicted label');
SVM的优点:
- 模型依赖的支持向量比较少,说明他们都是非常精致的模型,消耗内存少
- 一旦模型训练完成,预测阶段的速度非常快
- 由于模型只受边界线附近的点的影响,因此他们对于高维数据的学习效果非常好
- 与核函数方法的配合极具通用性,能够适用不同类型的数据
SVM的缺点:
- 随着样本量N的不断增加,最差的训练时间复杂度会达到 O [ N 3 ] \mathcal{O}[N^3] O[N3],即使经过高效处理后,也只能达到 O [ N 2 ] \mathcal{O}[N^2] O[N2]
- 训练效果非常依赖与边界软化参数C的选择是否合理
- 预测结果不能直接进行概率解释
专题:决策树与随机森林
随机森林的诱因:决策树
决策树采用非常直观的方式对事物进行分类或打标签:你只需问一系列问题就可以进行分类了
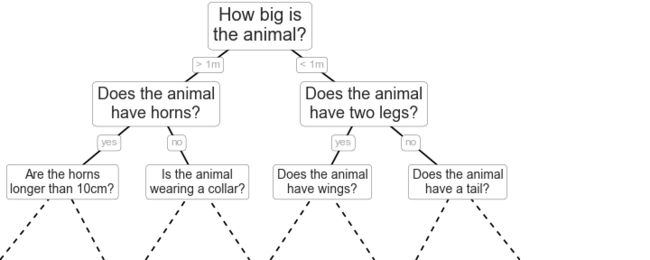
- 创建一颗决策树
在数据上构建的简单决策树不断将数据的一个特征或另一个特征按照某种判断条件进行分割
#创建二维数据
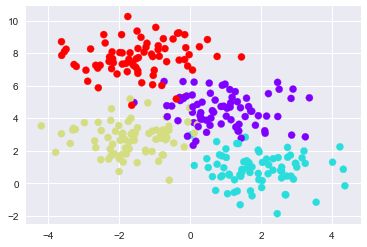
from sklearn.datasets import make_blobs
X,y=make_blobs(n_samples=300,centers=4,random_state=0,cluster_std=1.0)
plt.scatter(X[:,0],X[:,1],c=y,s=50,cmap='rainbow')
#使用sklearn中的决策树你和数据
from sklearn.tree import DecisionTreeClassifier
tree=DecisionTreeClassifier().fit(X,y)
#对分类结果可视化
def visualize_calssifier(model,X,y,ax=None,cmap='rainbow'):
ax = ax or plt.gca()
#画出训练数据
ax.scatter(X[:,0],X[:,1],c=y,s=30,cmap=cmap,clim=(y.min(),y.max()),zorder=3)
ax.axis('tight')
ax.axis('off')
xlim=ax.get_xlim()
ylim=ax.get_ylim()
#用评估器拟合数据
model.fit(X,y)
xx,yy=np.meshgrid(np.linspace(*xlim,num=200),np.linspace(*ylim,num=200))
Z=model.predict(np.c_[xx.ravel(),yy.ravel()]).reshape(xx.shape)
#为结果生成彩色图
n_classes=len(np.unique(y))
contours = ax.contourf(xx,yy,Z,alpha=0.3,levels=np.arange(n_classes+1)-0.5,cmap=cmap,clim=(y.min(),y.max()),zorder=1)
ax.set(xlim=xlim,ylim=ylim)
visualize_calssifier(DecisionTreeClassifier(),X,y)
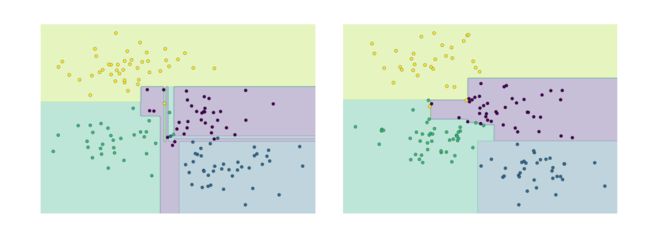
2. 决策树与过拟合
决策树非常容易陷得很深,因此往往会拟合局部数据,而没有对整个数据的大局观
下面是训练的两个不同的决策树,每棵树拟合一般的数据,显然在四个角有一只的记过,但在两类接壤的区域差异很大,这种不易往往都发生在分类比较模糊的地方因此将两棵树的结果组合起来,可能就会获得更好的结果
评估器集成算法:随机森林
通过组合多个过拟合评估器来降低过拟合程度的想法其实是一种集成学习方法,称为装袋算法
随机决策树的集成算法就是随机森林
使用BaggingClassifier元评估器来实现装袋分类器
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier
tree=DecisionTreeClassifier()
bag=BaggingClassifier(tree,n_estimators=100,max_samples=0.8,random_state=1)
visualize_calssifier(bag,X,y)
sklearn中的随机决策树集成算法的优化是通过RandomForestClassifier评估器实现的
from sklearn.ensemble import RandomForestClassifier
model=RandomForestClassifier(n_estimators=100,random_state=0)
visualize_calssifier(model,X,y)
随机森林回归
通过快慢震荡组合生成数据
rng=np.random.RandomState(42)
x=10*rng.rand(200)
def model(x,sigma=0.3):
fast_oscillation=np.sin(5*x)
slow_oscillation=np.sin(0.5*x)
noise=sigma*rng.randn(len(x))
return slow_oscillation+fast_oscillation+noise
y=model(x)
plt.errorbar(x,y,0.3,fmt='o');
通过随机森林回归器,获得拟合曲线
from sklearn.ensemble import RandomForestRegressor
forest=RandomForestRegressor(200)
forest.fit(x[:,None],y)
xfit=np.linspace(0,10,1000)
yfit=forest.predict(xfit[:,None])
ytrue=model(xfit,sigma=0)
plt.errorbar(x,y,0.3,fmt='o',alpha=0.5)
plt.plot(xfit,yfit,'-r')
plt.plot(xfit,ytrue,'-k',alpha=0.5)
真实模型是平滑曲线,而随机森林模型是锯齿线
案例:用随机森林识别手写数字
加载数据并显示
from sklearn.datasets import load_digits
digits=load_digits()
digits.keys()
fig=plt.figure(figsize=(6,6))
fig.subplots_adjust(left=0,right=1,bottom=0,top=1,hspace=0.05,wspace=0.05)
for i in range(64):
ax = fig.add_subplot(8,8,i+1,xticks=[],yticks=[])
ax.imshow(digits.images[i],cmap=plt.cm.binary,interpolation='nearest')
ax.text(0,7,str(digits.target[i]))
from sklearn.cross_validation import train_test_split
Xtrain, Xtest, ytrain, ytest = train_test_split(digits.data, digits.target,
random_state=0)
model = RandomForestClassifier(n_estimators=1000)
model.fit(Xtrain, ytrain)
ypred = model.predict(Xtest)
from sklearn import metrics
print(metrics.classification_report(ypred,ytest))
Out:
precision recall f1-score support
0 1.00 0.97 0.99 38
1 1.00 0.98 0.99 44
2 0.95 1.00 0.98 42
3 0.98 0.96 0.97 46
4 0.97 1.00 0.99 37
5 0.98 0.98 0.98 48
6 1.00 1.00 1.00 52
7 1.00 0.96 0.98 50
8 0.94 0.98 0.96 46
9 0.98 0.98 0.98 47
avg / total 0.98 0.98 0.98 450
绘制混淆矩阵
from sklearn.metrics import confusion_matrix
from sklearn.metrics import confusion_matrix
mat = confusion_matrix(ytest, ypred)
sns.heatmap(mat.T, square=True, annot=True, fmt='d', cbar=False)
plt.xlabel('true label')
plt.ylabel('predicted label');
随机森林的优点:
- 因为决策树的原理很简单,所以它的训练和预测速度都非常快,另外,多任务可以直接并行计算,因为每棵树都是完全独立的
- 多棵树可以进行概率分类:多个评估器之间的多数投票可以给出概率的估计值(使用sklearn中的predict_proba方法)
- 无参数模型很灵活,在其他评估器都七里河的任务中表现突出
随机森林的主要缺点在于其结果不太容易解释
专题:主成成分分析
rng = np.random.RandomState(1)
X = np.dot(rng.rand(2, 2), rng.randn(2, 200)).T
plt.scatter(X[:, 0], X[:, 1])
plt.axis('equal');
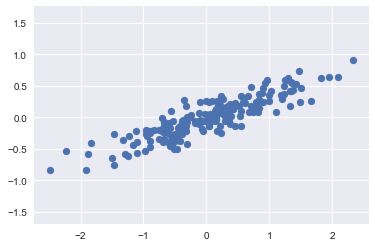
主成分分析中,一种量化两变量间关系的方法是在数据中找到一组主轴,并用这些主轴来描述数据集
pca中的重要指标是成分和可解释差异,成分定义向量的方向,可解释性差异定义向量的平方长度
from sklearn.decomposition import PCA
pca=PCA(n_components=2)
pca.fit(X)
print(pca.components_)
Out:
[[-0.94446029 -0.32862557]
[-0.32862557 0.94446029]]
print(pca.explained_variance_)
Out:
[0.7625315 0.0184779]
def draw_vector(v0,v1,ax=None):
ax= ax or plt.gca()
arrowprops=dict(arrowstyle='->',linewidth=2,shrinkA=0,shrinkB=0)
ax.annotate('',v1,v0,arrowprops=arrowprops)
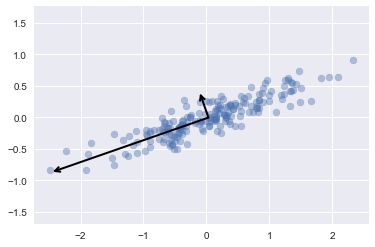
plt.scatter(X[:, 0], X[:, 1],alpha=0.4)
for length,vector in zip(pca.explained_variance_,pca.components_):
v=vector *3*np.sqrt(length)
draw_vector(pca.mean_,pca.mean_+v)
plt.axis('equal')
这些向量表示数据主轴,箭头长度表示输入数据中各个轴的重要程度,它衡量了数据投影到主轴上的方法的大小
- 用PCA降维
利用PCA降维
pca=PCA(n_components=1)
pca.fit(X)
X_pca=pca.transform(X)
print("original shape: ", X.shape)
print("transformed shape:", X_pca.shape)
Out:
original shape: (200, 2)
transformed shape: (200, 1)
降维可视化
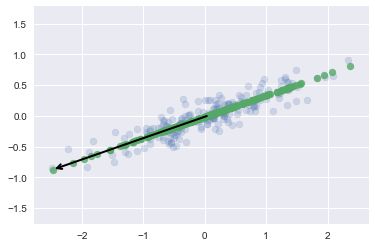
plt.scatter(X[:, 0], X[:, 1],alpha=0.2)
#对降维后的数据逆变换
X_new=pca.inverse_transform(X_pca)
plt.scatter(X_new[:, 0], X_new[:, 1],alpha=0.8)
for length,vector in zip(pca.explained_variance_,pca.components_):
v=vector *3*np.sqrt(length)
draw_vector(pca.mean_,pca.mean_+v)
plt.axis('equal')
PCA降维的含义:沿着最不重要的主轴的信息都被去除了,仅留下了含有最高方差值的数据成分
- 用PCA作数据可视化:手写数字
#手写数字是64维
digits.data.shape
Out:
(1797, 64)
pca=PCA(2)
projected=pca.fit_transform(digits.data)
plt.scatter(projected[:,0],projected[:,1],c=digits.target,edgecolors='none',alpha=0.5,cmap=plt.cm.get_cmap('Spectral',10))
plt.xlabel('component 1')
plt.ylabel('component 2')
plt.colorbar();
![]()
3. 成分的含义
训练集中的每副图像都是由一组64像素值的集合定义的
x = [ x 1 , x 2 , x 3 ⋯ x 64 ] x = [x_1, x_2, x_3 \cdots x_{64}] x=[x1,x2,x3⋯x64]
将向量的每个元素和对应描述的像素相乘,然后将这些结果加和就是这幅图像
i m a g e ( x ) = x 1 ⋅ ( p i x e l 1 ) + x 2 ⋅ ( p i x e l 2 ) + x 3 ⋅ ( p i x e l 3 ) ⋯ x 64 ⋅ ( p i x e l 64 ) {\rm image}(x) = x_1 \cdot{\rm (pixel~1)} + x_2 \cdot{\rm (pixel~2)} + x_3 \cdot{\rm (pixel~3)} \cdots x_{64} \cdot{\rm (pixel~64)} image(x)=x1⋅(pixel 1)+x2⋅(pixel 2)+x3⋅(pixel 3)⋯x64⋅(pixel 64)
数据的降维就是删除绝大部分元素,仅保留少量元素的基向量
如果我们仅使用前8个像素,我们会得到数据的8维投影,当近乎丢掉了90%的像素信息

这时就要选择其他基函数,这些基函数包含预定义的每个像素的贡献,PCA可以被认为是选择最优基函数的过程
i m a g e ( x ) = m e a n + x 1 ⋅ ( b a s i s 1 ) + x 2 ⋅ ( b a s i s 2 ) + x 3 ⋅ ( b a s i s 3 ) ⋯ image(x) = {\rm mean} + x_1 \cdot{\rm (basis~1)} + x_2 \cdot{\rm (basis~2)} + x_3 \cdot{\rm (basis~3)} \cdots image(x)=mean+x1⋅(basis 1)+x2⋅(basis 2)+x3⋅(basis 3)⋯
与像素基不同,PCA基可以通过为一个均值加上8个成分,来恢复输入图像最显著的特点
4. 选择成分的数量
将累计方差贡献率看做关于成分数量的函数,从而确定所需成分的数量
pca=PCA().fit(digits.data)
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance')
从图中可以看出大约20个成分可以保持90%的方差
用PCA作噪音过滤
创建手写数字数据绘制函数
def plot_digits(data):
fig,axes=plt.subplots(4,10,figsize=(10,4),subplot_kw={'xticks':[],'yticks':[]},gridspec_kw=dict(hspace=0.1,wspace=0.1))
for i ,ax in enumerate(axes.flat):
ax.imshow(data[i].reshape(8,8),cmap='binary',interpolation='nearest',clim=(0,16))
plot_digits(digits.data)
np.random.seed(42)
noisy=np.random.normal(digits.data,scale=4)
plot_digits(noisy)
使用噪音数据训练一个PCA,要求投影后保存50%的方差
pca=PCA(0.5).fit(noisy)
pca.n_components_
Out:
12
使用PCA计算出这些成分,然后利用逆变换重构过滤后的手写数字
components=pca.transform(noisy)
filtered=pca.inverse_transform(components)
plot_digits(filtered)
案例:特征脸
使用随机方法来估计前N个主成分,然后将前面的主成分的图像可视化
from sklearn.decomposition import PCA
pca=PCA(n_components=150,svd_solver='randomized')
pca.fit(faces.data)
fig,axes=plt.subplots(3,8,figsize=(9,4),subplot_kw={'xticks':[],'yticks':[]},gridspec_kw=dict(hspace=0.1,wspace=0.1))
for i,ax in enumerate(axes.flat):
ax.imshow(pca.components_[i].reshape(62,47),cmap='bone')
绘制累计方差曲线
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('number of components')
plt.ylabel('cumulative explained variance');
可以看出150个成分包含了90%的方差
对比利用这150个成分重构的图像和原始图像
pca=PCA(n_components=150,svd_solver='randomized').fit(faces.data)
components=pca.transform(faces.data)
projected=pca.inverse_transform(components)
# Plot the results
fig, ax = plt.subplots(2, 10, figsize=(10, 2.5),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i in range(10):
ax[0, i].imshow(faces.data[i].reshape(62, 47), cmap='binary_r')
ax[1, i].imshow(projected[i].reshape(62, 47), cmap='binary_r')
ax[0, 0].set_ylabel('full-dim\ninput')
ax[1, 0].set_ylabel('150-dim\nreconstruction');
PCA的主要弱点是经常受数据集的异常点影响
专题:流形学习
流形学习:“HELLO”
生成一些二位数据来定义一个流行
def make_hello(N=1000,rseed=42):
fig,ax=plt.subplots(figsize=(4,1))
fig.subplots_adjust(left=0,right=1,bottom=0,top=1)
ax.axis('off')
ax.text(0.5, 0.4, 'HELLO',va='center',ha='center',weight='bold',size=85)
fig.savefig('hello.png')
plt.close(fig)
from matplotlib.image import imread
data=imread('hello.png')[::-1,:,0].T
rng=np.random.RandomState(rseed)
X=rng.rand(4*N,2)
i,j=(X*data.shape).astype(int).T
mask=(data[i,j]<1)
X=X[mask]
X[:,0]*=(data.shape[0]/data.shape[1])
X=X[:N]
return X[np.argsort(X[:,0])]
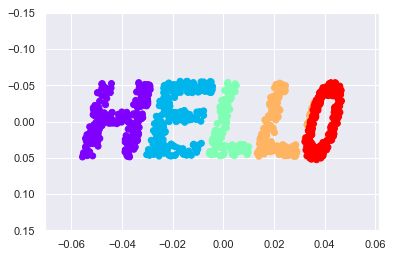
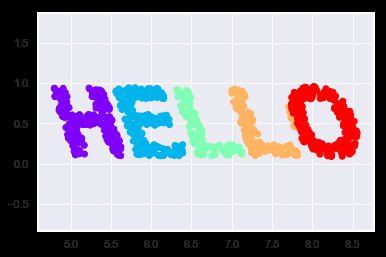
X = make_hello(1000)
colorize = dict(c=X[:, 0], cmap=plt.cm.get_cmap('rainbow', 5))
plt.scatter(X[:, 0], X[:, 1], **colorize)
plt.axis('equal');
多维标度法(MDS)
通过观察数据集,可以看到数据中选中的x值和y值并不是对数据的最基本的描述,即使放大、缩小或旋转数据,‘HELLO’依然会很明显
def rotate(X,angle):
theta=np.deg2rad(angle)
R=[[np.cos(theta),np.sin(theta)],[-np.sin(theta),np.cos(theta)]]
return np.dot(X,R)
X2=rotate(X,20)+5
plt.scatter(X2[:,0],X[:,1],**colorsize)
plt.axis('equal')
该例子的真正的基础特征是每个点与数据集中其它点的距离
使用Scikit-Learn中的pairwise_distances函数计算原始数据的关系矩阵
from sklearn.metrics import pairwise_distances
D=pairwise_distances(X)
D.shape
Out:
(1000, 1000)
plt.imshow(D,zorder=2,cmap='Blues',interpolation='nearest')
plt.colorbar()
可以看到旋转和变换的数据构建的距离矩阵是一样的
D2=pairwise_distances(X2)
np.allclose(D,D2)
Out:
True
MDS将一个数据集的距离矩阵还原成一个D维坐标来表示数据集
from sklearn.manifold import MDS
model = MDS(n_components=2, dissimilarity='precomputed', random_state=1)
out = model.fit_transform(D)
plt.scatter(out[:, 0], out[:, 1], **colorize)
plt.axis('equal');
将MDS用于流行学习
将数据映射到三维空间中
def random_projection(X,dimension=3,rseed=42):
assert dimension >=X.shape[1]
rng=np.random.RandomState(rseed)
C=rng.randn(dimension,dimension)
e,V=np.linalg.eigh(np.dot(C,C.T))
return np.dot(X,V[:X.shape[1]])
X3 = random_projection(X,3)
from mpl_toolkits import mplot3d
ax=plt.axes(projection='3d')
ax.scatter3D(X3[:,0],X3[:,1],X3[:,2],**colorsize)
ax.view_init(azim=70,elev=50)

使用MDS评估期输入三维数据,计算距离矩阵,然后得出距离矩阵的最优二维嵌入结果
model=MDS(n_components=2,random_state=1)
out3=model.fit_transform(X3)
plt.scatter(out3[:,0],out3[:,1],**colorsize)
plt.axis('equal')
非线性嵌入:当MDS失败时
将输入数据在三维空间扭曲成“S”的形状
def make_hello_s_curve(X):
t=(X[:,0]-2)*0.75*np.pi
x=np.sin(t)
y=X[:,1]
z=np.sign(t)*(np.cos(t)-1)
return np.vstack((x,y,z)).T
XS=make_hello_s_curve(X)
ax=plt.axes(projection='3d')
ax.scatter3D(XS[:,0],XS[:,1],XS[:,2],**colorsize)
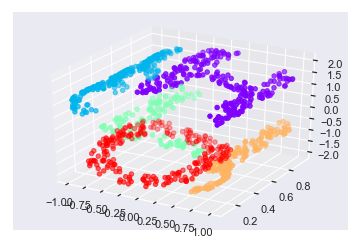
使用简单的MDS算法处理这个数据,发现无法展示数据非线性嵌入的特征,进而导致我们丢失了这个嵌入式流形的内部基本关系特征
model=MDS(n_components=2,random_state=2)
outS=model.fit_transform(XS)
plt.scatter(outS[:,0],outS[:,1],**colorsize)
plt.axis('equal')
非线性流形:局部线性嵌入
左图是MDS生成的嵌入模型,该方法保留所有的距离
右图是LLE生成的嵌入模型,该方法仅保留邻节点的距离
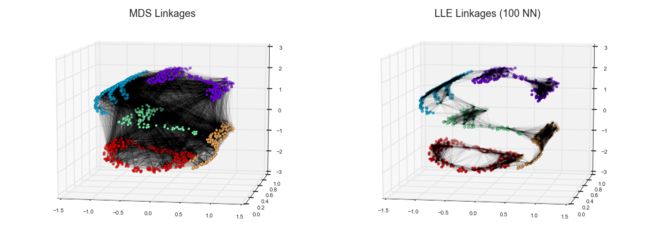
使用modified LLE对三维数据来还原嵌入的二维流形,通常情况下,modified LLE的效果比用其他算法还原定义好的流行数据的效果好,它几乎不会造成扭曲
from sklearn.manifold import LocallyLinearEmbedding
model=LocallyLinearEmbedding(n_neighbors=100,n_components=2,method='modified',eigen_solver='dense')
out=model.fit_transform(XS)
fig,ax=plt.subplots()
ax.scatter(out[:,0],out[:,1],**colorsize)
ax.set_ylim(0.15,-0.15)
关于流形方法的一些思考
由于流形学习在实际应用中的要求非常严格,因此处理在对高维数据进行简单的定性可视化之外,流形学习很少被正式使用
流形学习和PCA的对比:
- 在流形学习中,并没有好的框架来处理缺失值,相比之下PCA算法有一个用于处理缺失值的迭代方法
- 在流形学习中,数据中噪音的出现将会造成流形“短路”,并且严重影响嵌入结果。相比之下,PCA可以自然的从最重要的成分中滤除噪音
- 流形嵌入的结果通常高度依赖于所选取的邻节点的个数,并且通常没有确定的定量方式来选取最优的邻节点个数,相比之下PCA并不存在这样的问题
- 在流形学习中,全局最优的输出维度数很难确定,相比之下,PCA可以给予解释方差来确定输出的维度数
- 在流形学习中,嵌入维度的含义并不总是很清楚,而在PCA算法中,主成分有非常明确的含义
- 在流形学习中,流形方法的计算复杂度为 N [ O 2 ] N[O^2] N[O2]或 N [ O 3 ] N[O^3] N[O3],而PCA可以选择随机方法,通常速度更快
流形学习有个明显的有点就是可以保留数据中的非线性关系的能力,正因为这个原因,首先用PCA探索数据的线性特征,再使用流形方法探索数据的非线性特征
建议: - LLE对于简单问题例如S曲线、局部线性嵌入及变体的学习效果非常好
- Isomap对现实世界的高危数据源会有比较好的嵌入效果
- t-分布领域嵌入算法(t-SNE),在高度聚类的数据中效果较好,但是该方法比其他方法学习速度慢
示例:用Isomap处理人脸数据
在不同的投影位置输出图像的缩略图
from matplotlib import offsetbox
def plot_components(data,model,images=None,ax=None,thumb_frac=0.05,cmap='gray'):
ax=ax or plt.gca()
proj=model.fit_transform(data)
ax.plot(proj[:,0],proj[:,1],'.k')
if images is not None:
min_dist_2=(thumb_frac*max(proj.max(0)-proj.min(0)))**2
shown_images=np.array([2*proj.max(0)])
for i in range(data.shape[0]):
dist=np.sum((proj[i]-shown_images)**2,1)
if np.min(dist)<min_dist_2:
#不展示相距很近的点
continue
shown_images=np.vstack([shown_images,proj[i]])
imagebox=offsetbox.AnnotationBbox(offsetbox.OffsetImage(images[i],cmap=cmap),proj[i])
ax.add_artist(imagebox)
from sklearn.manifold import Isomap
fig,ax=plt.subplots(figsize=(10,10))
plot_components(faces.data,model=Isomap(n_components=2),images=faces.images[:,::2,::2])
可以看到图像明暗度从左到右持续变化,人脸朝向从上到下持续变化
示例:手写数字的可视化结构
加载数据,并计算这些数据的流形学习投影
from sklearn.datasets import load_digits
mnist=load_digits()
model=Isomap(n_components=2)
proj=model.fit_transform(mnist.data)
plt.scatter(proj[:,0],proj[:,1],c=mnist.target,cmap=plt.cm.get_cmap('jet',10))
plt.colorbar(ticks=range(10))
plt.clim(-0.5,9.5)
数据中数字1的Isomap嵌入
fig,ax=plt.subplots(figsize=(10,10))
data=mnist.data[mnist.target==1]
model=Isomap(n_neighbors=5,n_components=2,eigen_solver='dense')
plot_components(data,model,images=data.reshape((-1,8,8)),ax=ax,thumb_frac=0.05,cmap='gray_r')
![]()
专题:K-means聚类
K-means简介
K-means算法在不带标签的多维数据集中寻找确定数量的簇,最优的聚类记过需要符合以下两个假设:
- “簇中心点”是属于该簇的所有数据点坐标的算术平均值
- 一个簇的每个点到该簇中心点的距离,比到其他簇中心点的距离短
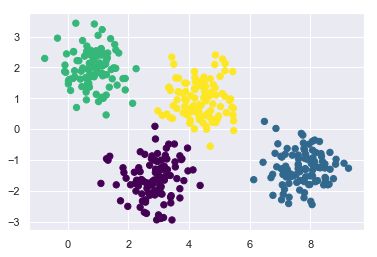
生成数据,并显示
from sklearn.datasets.samples_generator import make_blobs
X,y_true=make_blobs(n_samples=300,centers=4,cluster_std=0.60,random_state=0)
plt.scatter(X[:,0],X[:,1],s=50)
使用k-means算法自动完成4个簇的识别工作,并且展示聚类结果
from sklearn.cluster import KMeans
Kmeans=KMeans(n_clusters=4)
Kmeans.fit(X)
y_kmeans=Kmeans.predict(X)
plt.scatter(X[:,0],X[:,1],c=y_kmeans,s=50,cmap='viridis')
centers=Kmeans.cluster_centers_
plt.scatter(centers[:,0],centers[:,1],c='black',s=200,alpha=0.5)
K-means算法:期望最大化
K-means是期望最大化的一个非常简单并且易于理解的应用
期望最大化方法的步骤:
(1) 猜测一些簇中心点
(2) 重复直到收敛
- 期望步骤:将点分配至离其最近的簇中心点
- 最大化步骤:将簇中心点设置为所有点坐标的平均值
K-means的E-M算法的流程
K-means算法的实现
from sklearn.metrics import pairwise_distances_argmin
def find_clusters(X,n_clusters,rseed=2):
#随机选择簇中心
rng=np.random.RandomState(rseed)
i=rng.permutation(X.shape[0])[:n_clusters]
centers=X[i]
while True:
#基于最近的中心指定标签
labels=pairwise_distances_argmin(X,centers)
#根据点的平均值找到新的中心
new_centers=np.array([X[labels==i].mean(0) for i in range(n_clusters)])
#确认收敛
if np.all(centers == new_centers):
break
centers=new_centers
return centers,labels
centers,labels=find_clusters(X,4)
plt.scatter(X[:,0],X[:,1],c=labels,s=50,cmap='viridis')
使用期望最大化算法是的注意事项
- 可能不会达到全局最优算法
某些随机种子的初始值可能会导致很糟糕的结果
centers,labels=find_clusters(X,4,rseed=0)
plt.scatter(X[:,0],X[:,1],c=labels,s=50,cmap='viridis')
从上图可以看出虽然E-M算法最终收敛,但并没有收敛到全局最优配置,在sklearn中可以通过n_init参数设置尝试不同的初始值的次数
- 簇数量必须事先定好
K-means必须事先知道簇数量,它无法从数据中自动学习到簇的数量
labels=KMeans(6,random_state=0).fit_predict(X)
plt.scatter(X[:,0],X[:,1],c=labels,s=50,cmap='viridis')
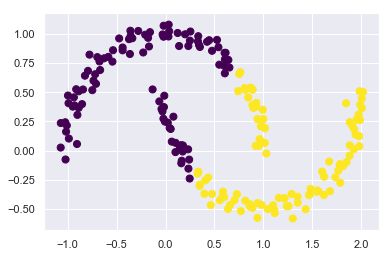
- K-means算法只能确定线性聚类边界
当簇中心点呈现非线性的复杂形状时,K-means算法通常不起作用
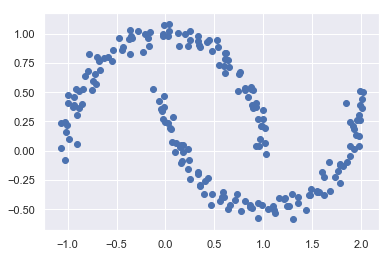
from sklearn.datasets import make_moons
X,y=make_moons(200,noise=0.05,random_state=0)
labels=KMeans(2,random_state=0).fit_predict(X)
plt.scatter(X[:,0],X[:,1],c=labels,s=50,cmap='viridis')
from sklearn.cluster import SpectralClustering
model=SpectralClustering(n_clusters=2,affinity='nearest_neighbors',assign_labels='kmeans')
labels=model.fit_predict(X)
plt.scatter(X[:,0],X[:,1],c=labels,s=50,cmap='viridis')
- 当数据量较大时,K-means会很慢
由于K-means的每次迭代必须获取数据集的所有的点,因此随着数据量的增大,算法会变得缓慢。可以使用批处理k-means算法,该算法每一步仅使用数据集的一个子集来更新簇中心点。
案例
- 案例1:用k-means算法处理手写数字
对手写数字数据使用K-means聚类,并将簇内中心点进行显示
from sklearn.datasets import load_digits
digits=load_digits()
from sklearn.cluster import KMeans
Kmeans=KMeans(n_clusters=10,random_state=0)
clusters=Kmeans.fit_predict(digits.data)
Kmeans.cluster_centers_.shape
fig,ax=plt.subplots(2,5,figsize=(8,3))
centers=Kmeans.cluster_centers_.reshape(10,8,8)
for axi,center in zip(ax.flat,centers):
axi.set(xticks=[],yticks=[])
axi.imshow(center,interpolation='nearest',cmap=plt.cm.binary)
![]()
将每个学习到的簇标签和真实标签进行匹配,并检查准确性
from scipy.stats import mode
labels=np.zeros_like(clusters)
for i in range(10):
mask=(clusters==i)
labels[mask]=mode(digits.target[mask])[0];
from sklearn.metrics import accuracy_score
accuracy_score(digits.target,labels)
Out:
0.7935447968836951
显示混淆矩阵,可以看出混淆的主要是1和8
from sklearn.metrics import confusion_matrix
mat=confusion_matrix(digits.target,labels)
sns.heatmap(mat.T,square=True,annot=True,fmt='d',cbar=False,xticklabels=digits.target_names,yticklabels=digits.target_names)
plt.xlabel('true label')
plt.ylabel('predicted label')
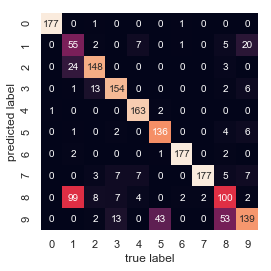
使用t-SNE对数据进行预处理,保留簇中的数据点,准确率可以达到94%
from sklearn.manifold import TSNE
#投影数据
tsne=TSNE(n_components=2,init='pca',random_state=0)
digits_proj=tsne.fit_transform(digits.data)
from sklearn.cluster import KMeans
kmeans=KMeans(n_clusters=10,random_state=0)
cluster=kmeans.fit_predict(digits_proj)
from scipy.stats import mode
labels=np.zeros_like(cluster)
for i in range(10):
mask=(cluster==i)
labels[mask]=mode(digits.target[mask])[0]
from sklearn.metrics import accuracy_score
accuracy_score(digits.target,labels)
Out:
0.9398998330550918
- 案例2:将k-means用于色彩压缩
图像中包含几百万种颜色,但大多数图像中的很大一部分色彩通常是不会被眼睛注意到的,而且图像中的很多像素都拥有类似或者相同的颜色
加载图像数据
from sklearn.datasets import load_sample_image
china=load_sample_image('china.jpg')
ax=plt.axes(xticks=[],yticks=[])
ax.imshow(china)
data=china/255.0 #转换成0~1区间
data=data.reshape(427*640,3)
def plot_pixels(data,title,colors=None,N=10000):
if colors is None:
colors=data
rng=np.random.RandomState(0)
i=rng.permutation(data.shape[0])[:N]
colors=colors[i]
R,G,B=data[i].T
fig,ax=plt.subplots(1,2,figsize=(16,6))
ax[0].scatter(R,G,color=colors,marker='.')
ax[0].set(xlabel='red',ylabel='green',xlim=(0,1),ylim=(0,1))
ax[1].scatter(R,B,color=colors,marker='.')
ax[1].set(xlabel='red',ylabel='blue',xlim=(0,1),ylim=(0,1))
fig.suptitle(title,size=20)
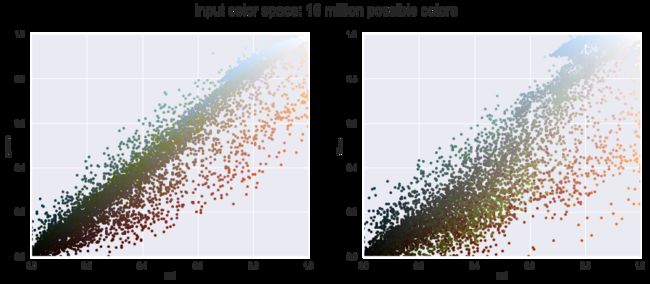
plot_pixels(data=data,title='input color space: 16 million possible colors')
from sklearn.cluster import MiniBatchKMeans
kmeans=MiniBatchKMeans(16)
kmeans.fit(data)
new_colors=kmeans.cluster_centers_[kmeans.predict(data)]
plot_pixels(data,colors=new_colors,title='reduced color space:16 colors')
使用计算的结果对原始像素重新着色
china_recolored=new_colors.reshape(china.shape)
fig,ax=plt.subplots(1,2,figsize=(16,6),subplot_kw=dict(xticks=[],yticks=[]))
fig.subplots_adjust(wspace=0.05)
ax[0].imshow(china)
ax[0].set_title('original image',size=16)
ax[1].imshow(china_recolored)
ax[1].set_title('16-color image',size=16)
专题:高斯混合模型
k-means算法的缺陷
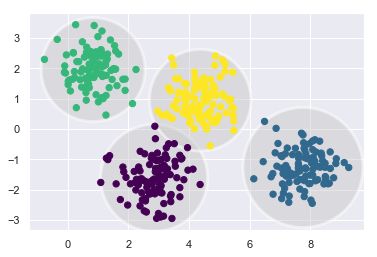
from sklearn.datasets.samples_generator import make_blobs
X,y_true = make_blobs(n_samples=400,centers=4,cluster_std=0.60,random_state=0)
X=X[:,::-1]
from sklearn.cluster import KMeans
kmeans=KMeans(4,random_state=0)
labels=kmeans.fit(X).predict(X)
plt.scatter(X[:,0],X[:,1],c=labels,s=40,cmap='viridis')
from scipy.spatial.distance import cdist
def plot_kmeans(kmeans,X,n_clusters=4,rseed=0,ax=None):
labels=kmeans.fit_predict(X)
ax=ax or plt.gca()
ax.axis('equal')
ax.scatter(X[:,0],X[:,1],c=labels,s=40,cmap='viridis',zorder=2)
centers=kmeans.cluster_centers_
radii=[cdist(X[labels==i],[center]).max() for i,center in enumerate(centers)]
for c, r in zip(centers,radii):
ax.add_patch(plt.Circle(c,r,fc='#CCCCCC',lw=3,alpha=0.5,zorder=1))
kmeans=KMeans(n_clusters=4,random_state=0)
plot_kmeans(kmeans,X)
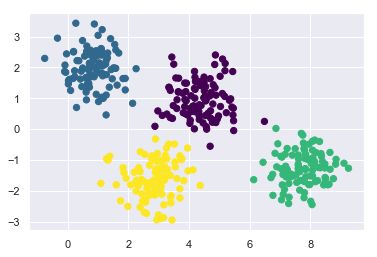
rng=np.random.RandomState(13)
X_stretched=np.dot(X,rng.randn(2,2))
kmeans=KMeans(n_clusters=4,random_state=0)
plot_kmeans(kmeans=kmeans,X=X_stretched)
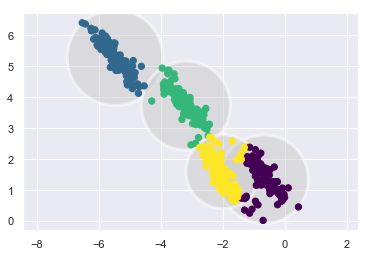
从上面的图可以看出k-means有一个重要的特征,它要求这些簇的模型必须是圆形,但这些变形的簇不是圆形的,因此拟合效果非常糟糕。
一般化E-M:高斯混合模型
高斯混合模型GMM试图找到多维高斯概率分布的混合体,从而获得任意数据集最好的模型
GMM同样使用的是期望最大化方法:
(1) 选择初始簇的中心位置和形状
(2) 重复知道收敛
a. 期望步骤(E-step):为每个点找到对应每个簇的概率作为权重
b. 最大化步骤(M-step):更新每个簇的位置,将其标准化,并且基于所有数据点的权重来确定形状
GMM详细解释参考:https://blog.csdn.net/manji_lee/article/details/41335307
高斯混合模型得到数据标签
from sklearn.mixture import GaussianMixture
gmm=GaussianMixture(n_components=4).fit(X)
labels=gmm.predict(X)
plt.scatter(X[:,0],X[:,1],c=labels,s=40,cmap='viridis')
probs=gmm.predict_proba(X)
probs[:5].round(3)
Out:
array([[0.537, 0. , 0.463, 0. ],
[0. , 0. , 0. , 1. ],
[0. , 0. , 0. , 1. ],
[1. , 0. , 0. , 0. ],
[0. , 0. , 0. , 1. ]])
绘制椭圆的函数
from matplotlib.patches import Ellipse
def draw_ellipst(position,covariance,ax=None,**kwargs):
ax= ax or plt.gca()
if covariance.shape==(2,2):
U,s,Vt=np.linalg.svd(covariance)
angle=np.degrees(np.arctan2(U[1,0],U[0,0]))
width,height=2*np.sqrt(s)
else:
angle=0
width,height=2*sqrt(covariance)
for nsig in range(1,4):
ax.add_patch(Ellipse(position,nsig*width,nsig*height,angle,**kwargs))
def plot_gmm(gmm,X,label=True,ax=None):
ax = ax or plt.gca()
labels=gmm.fit_predict(X)
if label:
ax.scatter(X[:,0],X[:,1],c=labels,s=40,cmap='viridis',zorder=2)
else:
ax.scatter(X[:,0],X[:,1],s=40,zorder=2)
ax.axis('equal')
w_factor=0.2/gmm.weights_.max()
for pos,covar,w in zip(gmm.means_,gmm.covariances_,gmm.weights_):
draw_ellipst(pos,covar,alpha=w*w_factor)
使用GMM处理初始数据
gmm=GaussianMixture(n_components=4,random_state=42)
plot_gmm(gmm,X)
plot_gmm(gmm,X_stretched)
参数covariance_type='full’可以控制每个簇的形状自由度
'full'
each component has its own general covariance matrix
'tied'
all components share the same general covariance matrix
'diag'
each component has its own diagonal covariance matrix
'spherical'
each component has its own single variance
将GMM用作密度估计
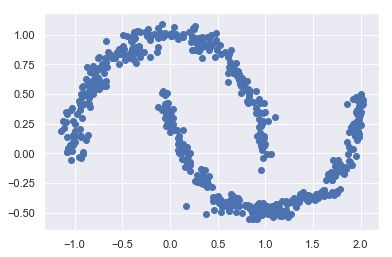
使用make_moons函数生成一些数据
from sklearn.datasets import make_moons
Xmoon,ymoon=make_moons(200,noise=0.05,random_state=0)
plt.scatter(Xmoon[:,0],Xmoon[:,1])
gmm2=GaussianMixture(n_components=2,covariance_type='full',random_state=0)
plot_gmm(gmm2,Xmoon)
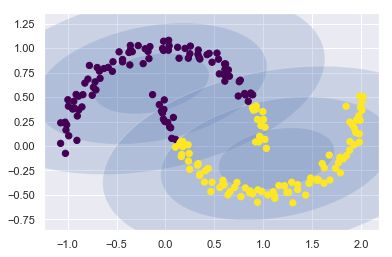
选用更多的成分而忽视簇标签,就可以找到一个更将近输入数据的拟合结果
gmm16=GaussianMixture(n_components=16,covariance_type='full',random_state=0)
plot_gmm(gmm16,Xmoon,label=False)
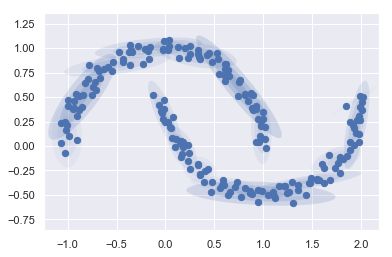
使用GMM拟合原始数据获得的16个成分生成600个新的数据点
Xnew=gmm16.sample(n_samples=600)
plt.scatter(Xnew[0][:,0],Xnew[0][:,1])
GMM作为一种生成模型,提供了一种确定数据集最优成分数量的方法
AIC是赤池信息量准则,可以权衡所估计模型的复杂度和此模型拟合数据的优良性
BIC是贝叶斯信息准则,对模型的拟合效果进行评价的一个指标,BIC值越小,则模型对数据的拟合越好
类的最优数量出现在AIC或BIC曲线最小值 的位置
n_components=np.arange(1,21)
models=[GaussianMixture(n,covariance_type='full',random_state=0).fit(Xmoon) for n in n_components]
plt.plot(n_components,[m.bic(Xmoon) for m in models],label='BIC')
plt.plot(n_components,[m.aic(Xmoon) for m in models],label='AIC')
plt.legend(loc='best')
plt.xlabel('n_components')
示例:用GMM生成新的数据
加载手写数字
def plot_digits(data):
fig,ax=plt.subplots(10,10,figsize=(8,8),subplot_kw=dict(xticks=[],yticks=[]))
fig.subplots_adjust(hspace=0.05,wspace=0.05)
for i,axi in enumerate(ax.flat):
im=axi.imshow(data[i].reshape(8,8),cmap='binary')
im.set_clim(0,16)
plot_digits(digits.data)
GMM在高维空间可能不太容易收敛,因此先使用PCA降维,保留样本数据99%的方差
from sklearn.decomposition import PCA
pca=PCA(0.99,whiten=True)
data=pca.fit_transform(digits.data)
data.shape
Out:
(1797, 41)
通过AIC和BIC确定成分数量
n_components=np.arange(50,210,10)
models=[GaussianMixture(n,covariance_type='full',random_state=0).fit(data) for n in n_components]
plt.plot(n_components,[m.aic(data) for m in models],label='AIC')
plt.plot(n_components,[m.bic(data) for m in models],label='bic')
确认已经收敛
gmm=GaussianMixture(110,random_state=0)
gmm.fit(data)
print(gmm.converged_)
Out:
True
生成新的数据
data_new=gmm.sample(100)
digits_new=pca.inverse_transform(data_new[0])
plot_digits(digits_new)
![]()
专题:核密度估计
KDE的由来:直方图
密度评估器是一种寻找数据集生成概率分布模型的算法
直方图就是一个简单的密度评估期
def make_data(N,f=0.3,rseed=1):
rand=np.random.RandomState(rseed)
x=rand.randn(N)
x[int(f*N):]+=5
return x;
x=make_data(1000)
hist=plt.hist(x,bins=30,density=True)
在区间不变的情况下,标准化只是简单的改变了y轴的比例
![]()
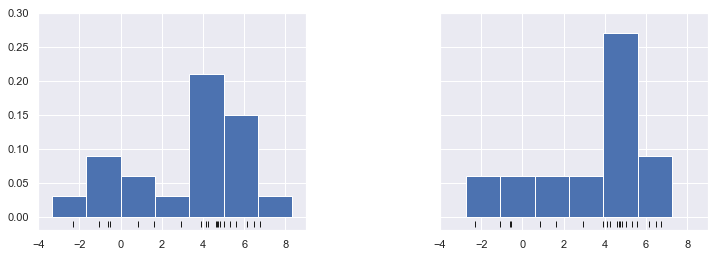
当改变区间后,会出现完全不一样的直方图
x=make_data(20)
bins=np.linspace(-5,10,10)
fig,ax=plt.subplots(1,2,figsize=(12,4),sharex=True,sharey=True,subplot_kw={'xlim':(-4,9),'ylim':(-0.02,0.3)})
fig.subplots_adjust(wspace=0.5)
for i,offset in enumerate([0.0,0.6]):
ax[i].hist(x,bins=bins+offset,density=True)
ax[i].plot(x,np.full_like(x,-0.01),'|k',markeredgewidth=1)
x_d=np.linspace(-4,8,2000)
density=sum((abs(xi-x_d)<0.5) for xi in x)
plt.fill_between(x_d,density,alpha=0.5)
plt.plot(x,np.full_like(x,-0.1),'|k',markeredgewidth=1)
plt.axis([-4,8,-0.2,8]);
‘
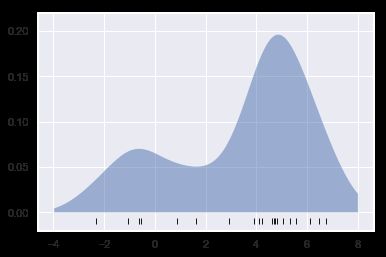
使用高斯核进行密度估计
from scipy.stats import norm
x_d=np.linspace(-4,8,1000)
density=sum(norm(xi).pdf(x_d) for xi in x)
plt.fill_between(x_d,density,alpha=0.5)
plt.plot(x,np.full_like(x,-0.1),'|k',markeredgewidth=1)
plt.axis([-4,8,-0.2,8]);
核密度估计的实际应用
核密度估计的自由参数是核类型参数,它可以指定每个点核密度分布的形状
核宽度参数控制每个点的核大小
sklearn中的KernelDensity重现前面的结果
from sklearn.neighbors import KernelDensity
#初始化并拟合KDE模型
kde=KernelDensity(bandwidth=1.0,kernel='gaussian')
kde.fit(x[:,None])
#score_samples返回概率密度的对数值
logprob=kde.score_samples(x_d[:,None])
plt.fill_between(x_d,np.exp(logprob),alpha=0.5)
plt.plot(x,np.full_like(x,-0.01),'|k',markeredgewidth=1)
plt.ylim(-0.02,0.22)
KDE中,带宽的选择不仅对找到合适的密度估计非常重要,也是在密度估计总控制偏差-方差平衡的关键:带宽过窄将导致估计呈现高方差(过拟合),而且每个点的出现或缺失都会引起很大的不同;带宽过宽将导致估计呈现高偏差(欠拟合),而且带宽较大的核还会破坏数据结构
在sklearn中可以使用GridSearchCV来优化数据集的密度估计带宽
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import LeaveOneOut
bandwidths=10*np.linspace(-1,1,100)
grid=GridSearchCV(estimator=KernelDensity(kernel='gaussian'),param_grid={'bandwidth':bandwidths},cv=LeaveOneOut())
grid.fit(x[:,None]);
grid.best_params_
Out:
{'bandwidth': 1.1111111111111116}
示例:球形空间的KDE
KDE最常用的是描述数据点的分布
加载褐喉树懒和森林小稻鼠这两种南美洲哺乳类动物的地理分布观测值
from sklearn.datasets import fetch_species_distributions
data=fetch_species_distributions()
latlon=np.vstack([data.train['dd lat'],data.train['dd long']]).T
species=np.array([d.decode('ascii').startswith('micro') for d in data.train['species']],dtype='int')
使用Basemap工具在南美洲地图中画出这两个物种的观测位置
#当导入basemap时出现KeyError: 'PROJ_LIB'时添加下面两句
import os
os.environ['PROJ_LIB']=r'D:\Anaconda3\pkgs\proj4-5.1.0-hfa6e2cd_1\Library\share'
from mpl_toolkits.basemap import Basemap
from sklearn.datasets.species_distributions import construct_grids
xgrid,ygrid=construct_grids(data)
#用Basemap画出海岸线
m=Basemap(projection='cyl',resolution='c',llcrnrlat=ygrid.min(),urcrnrlat=ygrid.max(),llcrnrlon=xgrid.min(),urcrnrlon=xgrid.max())
m.drawmapboundary(fill_color='#DDEEFF')
m.fillcontinents(color='#FFEEDD')
m.drawcoastlines(color='gray',zorder=2)
m.drawcounties(color='gray',zorder=2)
#画出位置
m.scatter(latlon[:,1],latlon[:,0],zorder=3,c=species,cmap='rainbow',latlon=True)
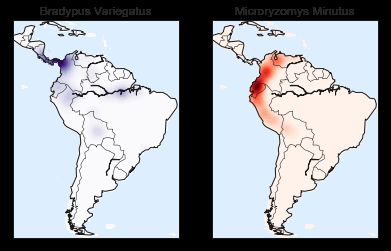
使用核密度估计可以在地图中平滑的显示密度
from sklearn.neighbors import KernelDensity
#准备画轮廓图的数据点
X,Y=np.meshgrid(xgrid[::5],ygrid[::5][::-1])
land_reference=data.coverages[6][::5,::5]
land_mask=(land_reference>-9999).ravel()
xy=np.vstack([Y.ravel(),X.ravel()]).T
xy=np.radians(xy[land_mask])
#创建两幅并排的图
fig,ax=plt.subplots(1,2)
fig.subplots_adjust(left=0.05,right=0.95,wspace=0.05)
species_names=['Bradypus Variegatus','Microryzomys Minutus']
cmap=['Purples','Reds']
for i,axi in enumerate(ax):
axi.set_title(species_names[i])
#用Basemap画出海岸线
m=Basemap(projection='cyl',resolution='c',llcrnrlat=Y.min(),urcrnrlat=Y.max(),llcrnrlon=X.min(),urcrnrlon=X.max(),ax=axi)
m.drawmapboundary(fill_color='#DDEEFF')
m.drawcoastlines()
m.drawcountries()
#构建一个球形的分布核密度估计
kde=KernelDensity(bandwidth=0.03,metric='haversine')
kde.fit(np.radians(latlon[species==i]))
#只计算大陆的值:-9999表示海洋
Z=np.full(land_mask.shape[0],-9999.0)
Z[land_mask]=np.exp(kde.score_samples(xy))
Z=Z.reshape(X.shape)
#画出密度的轮廓
levels=np.linspace(0,Z.max(),25)
axi.contourf(X,Y,Z,levels=levels,cmap=cmap[i])
示例:不是很朴素的贝叶斯
一般分类器的生成算法:
(1) 通过标签分割训练数据
(2) 为每个数据拟合一个KDE来获取数据的生成模型,这样就可以用任意x观察值和y标签计算出似然估计值P(x|y)
(3) 根据训练样本中每个类的样本数量,计算每一类的先验概率P(y)
(4) 对于一个未知的点x,每个类的后验概率 P ( y ∣ x ) ∝ P ( x ∣ y ) P ( y ) P(y~|~x) \propto P(x~|~y)P(y) P(y ∣ x)∝P(x ∣ y)P(y),而后验概率最大的类就是分配给该店的标签
定义KDE分类器
from sklearn.base import BaseEstimator,ClassifierMixin
class KDEClassifier(BaseEstimator, ClassifierMixin):
"""基于KDE的贝叶斯生成分类
参数
——————————
bandwidth:float 每个类中的核宽度
kernel:str 核函数的名称,传递给KernelDensity
"""
def __init__(self, bandwidth=1.0, kernel='gaussian'):
self.bandwidth = bandwidth
self.kernel = kernel
def fit(self,X,y):
self.classes_=np.sort(np.unique(y))
training_sets=[X[y==yi] for yi in self.classes_]
self.models_=[KernelDensity(bandwidth=self.bandwidth, kernel=self.kernel).fit(Xi) for Xi in training_sets]
self.logpriors_=[np.log(Xi.shape[0]/X.shape[0]) for Xi in training_sets]
return self
def predict_proba(self,X):
logprobs=np.array([model.score_samples(X) for model in self.models_]).T
result = np.exp(logprobs + self.logpriors_)
return result/result.sum(1,keepdims=True)
def predict(self, X):
return self.classes_[np.argmax(self.predict_proba(X), 1)]
使用自定义的分类器
from sklearn.datasets import load_digits
from sklearn.grid_search import GridSearchCV
digits=load_digits()
bandwidths=10**np.linspace(0,2,100)
grid=GridSearchCV(KDEClassifier(),{'bandwidth':bandwidths})
grid.fit(digits.data,digits.target)
scores=[val.mean_validation_score for val in grid.grid_scores_]
plt.semilogx(bandwidths,scores)
plt.xlabel('bandwidth')
plt.ylabel('accuracy')
plt.title('KDE model performance')
print(grid.best_params_)
print(grid.best_score_)
Out:
{'bandwidth': 7.054802310718643}
0.9666110183639399
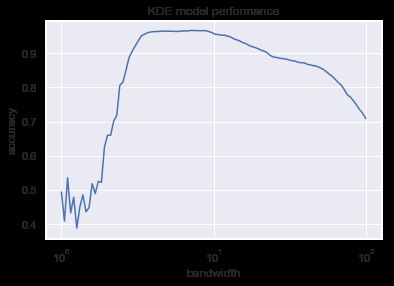
从图中可以看到这个不是很朴素的贝叶斯分类器的交叉验证准确率达到了96%
应用:人脸识别管道
方向梯度直方图(HOG)
https://www.cnblogs.com/hrlnw/archive/2013/08/06/2826651.html
HOG特征
HOG方法:
- 图像标准化,消除照度对图像的影响
- 用与水平和垂直方向的亮度梯度相关的两个过滤器处理图像,捕捉图像的边、角和纹理信息
- 将图像切割成预定义大象的图块,然后计算每个图块内梯度方向的频次直方图
- 对比每个图块与相邻图块的频次直方图,并做标准化处理,进一步消除照度对图像的影响
- 获得描述每个图块信息的一维特征向量
scikit-image项目内置了一个快速的HOG提取器
from skimage import data,color,feature
import skimage.data
image=color.rgb2gray(data.chelsea())
hog_vec,hog_vis=feature.hog(image,visualize=True)
fig,ax=plt.subplots(1,2,figsize=(12,6),subplot_kw=dict(xticks=[],yticks=[]))
ax[0].imshow(image,cmap='gray')
ax[0].set_title('input image')
ax[1].imshow(hog_vis)
ax[1].set_title('visualization of HOG ')
HOG实战:简单人脸识别器
使用线性支持向量机和HOG特征:
- 获取一组人脸图像缩略图,构建positive训练样本
- 获取另一组人脸图像缩略图,构建negative训练样本
- 提取训练样本的HOG特征
- 对样本训练一个线性SVM模型
- 为未知图像传递一个移动的窗口,用模型评估窗口中的内容是否是人脸
获取一组正训练样本
from sklearn.datasets import fetch_lfw_people
faces=fetch_lfw_people()
positive_patches=faces.images
positive_patches.shape
Out:
(13233, 62, 47)
获取一组负训练样本
使用sickit-image的图像数据,再用scikit-image的PatchExtractor提取缩略图
from skimage import data,transform
imgs_to_use = ['camera', 'text', 'coins', 'moon',
'page', 'clock', 'immunohistochemistry',
'chelsea', 'coffee', 'hubble_deep_field']
images=[color.rgb2gray(getattr(data,name)()) for name in imgs_to_use ]
from sklearn.feature_extraction.image import PatchExtractor
def extract_patches(img,N,scale=1.0,patch_size=positive_patches[0].shape):
extracted_patch_size=tuple((scale*np.array(patch_size)).astype(int))
extractor=PatchExtractor(patch_size=extracted_patch_size,max_patches=N,random_state=0)
patches=extractor.transform(img[np.newaxis])
if scale !=1:
patches=np.array([transform.resize(patch,patch_size) for patch in patches])
return patches
negative_patches=np.vstack([extract_patches(im,1000,scale) for im in images for scale in [0.5,1.0,2.0]])
negative_patches.shape
Out:
(30000, 62, 47)
fig,ax=plt.subplots(6,10)
for i,axi in enumerate(ax.flat):
axi.imshow(negative_patches[500*i],cmap='gray')
axi.axis('off')
这些样本可以让算法学习没有人脸是什么样子
组合数据集并提取HOG特征
from itertools import chain
X_train = np.array([feature.hog(im) for im in chain(positive_patches,negative_patches)])
y_train=np.zeros(X_train.shape[0])
y_train[:positive_patches.shape[0]]=1
X_train.shape
Out:
(43233, 1215)
训练一个支持向量机
使用简单的高斯朴素贝叶斯分类器,已经可以得到90%以上的准确率
from sklearn.naive_bayes import GaussianNB
from sklearn.cross_validation import cross_val_score
cross_val_score(GaussianNB(),X_train,y_train)
Out:
array([0.94094789, 0.87481785, 0.93969884])
使用网格搜索获取最优的边界软化参数C
from sklearn.svm import LinearSVC
from sklearn.grid_search import GridSearchCV
grid=GridSearchCV(LinearSVC(),{'C':[1.0,2.0,4.0,8.0]})
grid.fit(X_train,y_train)
print(grid.best_params_)
print(grid.best_score_)
Out:
{'C': 4.0}
0.986584322161312
用最优评估器重新训练数据集
model=grid.best_estimator_
model.fit(X_train,y_train)
Out:
LinearSVC(C=4.0, class_weight=None, dual=True, fit_intercept=True,
intercept_scaling=1, loss='squared_hinge', max_iter=1000,
multi_class='ovr', penalty='l2', random_state=None, tol=0.0001,
verbose=0)
在新图像中寻找人脸
test_image=skimage.data.astronaut()
test_image=skimage.color.rgb2gray(test_image)
test_image=skimage.transform.rescale(test_image,0.5,multichannel=False,anti_aliasing=False)
test_image=test_image[:160,40:180]
plt.imshow(test_image,cmap='gray')
plt.axis('off')

创建一个不断在图像中移动的窗口,然后计算每次移动位置的HOG特征
def sliding_window(img,patch_size=positive_patches[0].shape,istep=2,jstep=2,scale=1.0):
Ni,Nj=(int(scale*s) for s in patch_size)
for i in range(0,img.shape[0]-Ni,istep):
for j in range(0,img.shape[1]-Ni,jstep):
patch=img[i:i+Ni,j:j+Nj]
if scale!=1:
patch=transform.resize(patch,patch_size)
yield(i,j),patch
indices,patches=zip(*sliding_window(test_image))
patches_hog=np.array([feature.hog(patch) for patch in patches])
patches_hog.shape
Out:
(1911, 1215)
labels=model.predict(patches_hog)
labels.sum()
Out:
33.0
fig,ax=plt.subplots()
ax.imshow(test_image,cmap='gray')
ax.axis('off')
Ni,Nj=positive_patches[0].shape
indices=np.array(indices)
for i,j in indices[labels==1]:
ax.add_patch(plt.Rectangle((j,i),Ni,Nj,edgecolor='red',alpha=0.3,lw=2,facecolor='none'))
注意事项与改进方案
- 训练集,尤其是负样本训练集不完整,有许多类似人脸的纹理并不在训练集中,因此模型非常容易产生假正错误
- 目前的管道只搜索一个尺寸
- 应该将包含人脸的重叠窗口合并
- 管道可以更具流线型
- 考虑深度学习技术