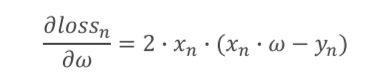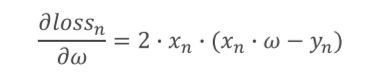梯度下降算法以及随机梯度下降算法的原理及python代码

梯度下降算法 

梯度下降，依照所给数据，判断函数，随机给一个初值w，之后通过不断更改，一步步接近原函数的方法。更改的过程也就是根据梯度不断修改w的过程。

以简单的一元函数为例

原始数据为

x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]

因此我们设置函数为

对于该函数，我们的w是未知的，因此如何根据xy的数据，获取到正确的w值就是梯度下降的目标。

首先我们要先给定一个随机w值，这个值可以是任何数，我们的算法就会根据我们所计算的cost函数，判断偏离正确数据有多大，之后根据梯度，对w进行更新，直到cost为0，我们也就获取到正确的w值。

cost函数，也就是根据自己的模拟量，算出的结果与原函数所给数据的差值的平方

cost函数的表示为（所求的是N个数据的平均cost）

cost函数对w的求导为

每次更改的过程就是不断更新w，（a也就是每次w改变的步长，用a乘以w的偏导）

最终当cost为0时，就基本可以保证函数模拟的是正确的。

梯度下降的python实现

x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]
w = 1.0

def forward(x):
    return x*w
def cost(xs,ys):
    cost = 0
    for x,y in zip(xs,ys):
        y_pred = forward(x)
        cost+=(y_pred - y) **2
    return cost / len(xs)
    '''求平均的cost大小'''


def gradient(xs,ys):
    grad = 0
    for x,y in zip(xs,ys):
        grad += 2*x*(x*w -y)
    return grad/len(xs)
    '''求平均的梯度大小'''

print("Predict (before training)",4,forward(4))
for epoch in range(100):
    cost_val = cost(x_data,y_data)
    grad_val = gradient(x_data,y_data)
    w-=0.1*grad_val
    print('EPOCH:',epoch,'w=',w,'loss=',cost_val)
print("Predict(after training)",4,forward(4))
'''对下一个数据进行预测的结果'''

由于梯度算法，是对所有的差值求平均，因此，很有可能困在局部最优解之中。举个例子，一个人在下山的过程中，不断找周围的最低点，有的人可以直接下山，但是有的人在半山腰山遇到一个水池，对这个水池来说，四周都比它高，因此，就会被困在这个水池中，没法下山。因此解决办法就是随机梯度下降。

随机梯度下降

采用随机梯度下降，相较于求平均的cost，采用随机的loss函数，也就是每次只取一个值，还是上个例子，当这个人困在水池中是，突然随机出现一个点，告诉你你的周围还有更低点，你就可以走出水池，然后重新走向下山的道路

求w的导数函数

loss函数

对于x，y参数，不像梯度下降的cost函数要遍历x，y的原数据，而只是使用当前的数据x,y即可

随机梯度下降的python实现

x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]
w = 1.0

def forward(x):
    return x*w

def loss(x,y):
    y_pred = forward(x)
    return(y_pred-y)**2

def gradient(x,y):
    return 2*x*y*(x*w-y)

print('Predict(before training)',4,forward(4))
for epoch in range(100):
    for x,y in zip(x_data,y_data):
'''相比于梯度下降需要一次对所有数据求取平均值，随机梯度下降需要进行两次循环,
    在第二次循环中，对于每个数据都要单独求取一个梯度'''
        grad = gradient(x,y)
        w = w-0.01*grad
        print("grad:",grad)
        '''分别对三个数据求取梯度'''
        l = loss(x,y)
    print("progress:",epoch,"w=",w,"loss",l)
print("Prediect (after training)",4,forward(4))