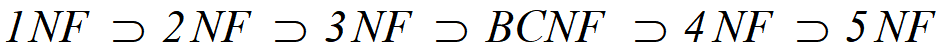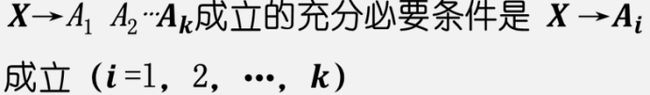《数据库系统概论》 第6章——关系数据理论（重点）
虽然写这个博客主要目的是为了给我自己做一个思路记忆录，但是如果你恰好点了进来，那么先对你说一声欢迎。我并不是什么大触，只是一个菜菜的学生，如果您发现了什么错误或者您对于某些地方有更好的意见，非常欢迎您的斧正！
目录
6.1问题的提出
①回顾关系模型
②数据依赖
6.2规范化
6.2.1函数依赖
6.2.2码
6.2.3范式
6.2.4 2NF
6.2.5 3NF（不存在传递函数依赖）
6.2.6 BCNF
以下是自己对三范式以及BCNF的理解（如果为了理解，建议直接看这里）
6.2.9规划范小结
6.3数据依赖的公理系统
Armstrong公理系统
导出规则
引理6.1
引理6.2
√求闭包的算法
极小化过程
6.4模式的分解
6.1问题的提出
▶针对具体问题，如何构造一个适合于它的数据模式
1） 应该构造几个关系模式；
2） 每一个关系应该由哪一些属性组成。
▶数据库逻辑设计的工具──关系数据库的规范化理论
①回顾关系模型
关系 关系模式 关系数据库 关系数据库的模式
▶关系模式由五部分组成，即它是一个五元组：R(U, D, DOM, F)
R： 关系名（符号化的元组语义）
U： 组成该关系的属性名集合
D： 属性组U中属性所来自的域（不重要）
DOM： 属性向域的映象集合（不重要）
F： 属性间数据的依赖关系集合
▶关系模式R(U, D, DOM, F) 可以简化为一个三元组：R(U,F)
当且仅当U上的一个关系r满足F时，r称为关系模式R(U,F)的一个关系。
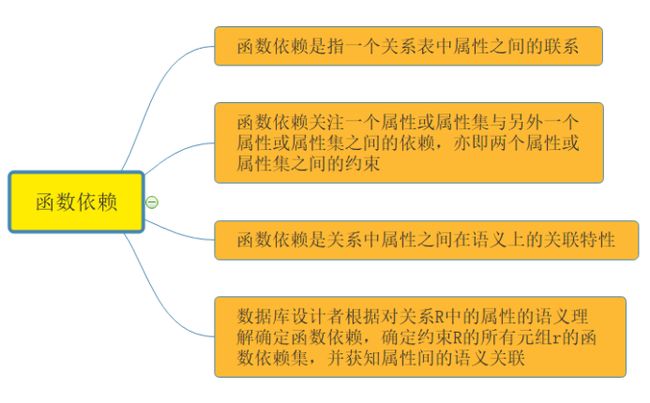
②数据依赖
6.2规范化
6.2.1函数依赖
①符号说明：
R：一个关系模式
U={A1,A2,...,An}:R的所有属性的集合；
F：R中函数依赖的集合
R：R所取的值
t[X]：元组t在属性X上的取值。例如t[Dname]=’HuangKai’
②函数依赖的定义
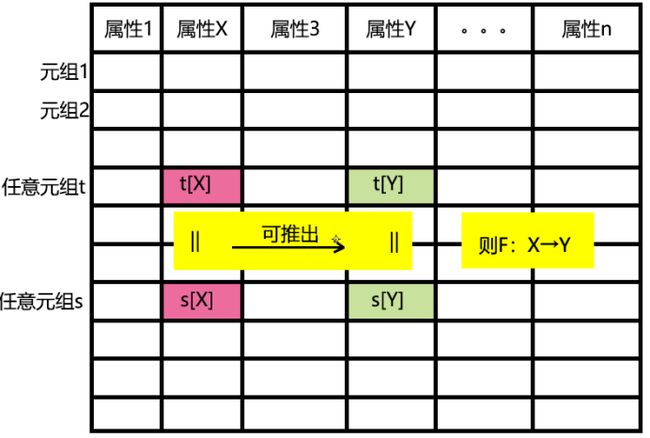
（如果不想看底下这段长文字的，可以直接看图）
设有一个关系模式R(U)，X，Y为其属性U的子集，即X
U，Y
U，设t，s是关系R中的任意两个元组，如果t[X]=s[X]，则t[Y]=s[Y]，那么称Y函数依赖于X，或X函数决定Y，也可称F：X→Y在关系模式R(U)上成立。
例子：X是出生年月，Y是年龄，显然知道了X就可以知道Y。
平凡的函数依赖必然成立，它不反应任何语义，若不特别声明，总是讨论非平凡的函数依赖。
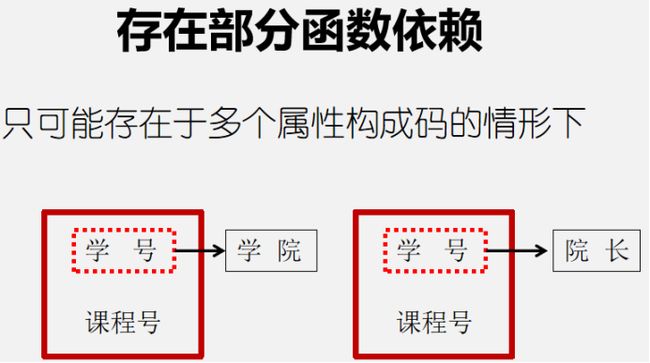
③完全函数依赖与部分函数依赖
④传递函数依赖
例6.1：建立一个描述学校教务的数据库：
学号（Sno）、所在系（Sdept）、系主任姓名（Mname）
课程号（Cno）、成绩（Grade）
单一的关系模式 Student
U ＝｛ Sno, Sdept, Mname, Cno, Grade ｝
数据之间的关系有（语义）：
1） 一个系有若干个学生，一个学生只属于一个系；
2） 一个系只有一名系主任；
3） 一个学生可以选修多门课程；
4） 每个学生选修的每门课程有一个成绩。
6.2.2码
√码在之前已经提到过了，书本P39对“码”的定义为：能唯一标识一个元组的属性组。（比如一个学生基本情况表，只要学号和姓名都确定了，那么其它属性也就确定了，在这种情况下，学号与姓名组成的属性组就称为码）
①用函数依赖定义码
√设K为R
（U对K完全依赖），则K称为R的候选码（Candidate Key）。
√若候选码多于一个，则选定其中一个作为主码。
②主属性与非主属性（全码、外码）
√主属性（Prime attribute）：包含在任何一个候选码中的属性（K属性组中的任何一个属性）
√非主属性（Nonprime attribute）或非码属性（Non-key attribute）：不包含在任何候选码中的属性（不属于K属性组中的任何一个属性）
√全码（All-key）：整个属性组是码。（没有哪个属性或属性组可以单独决定另外的所有属性）
√外码（foreign key）：在SC（Sno，Cno，Grade）中，Sno不是码，但在关系模式S（Sno，Sdept，Sage）中是码，则Sno是关系模式SC的外码。
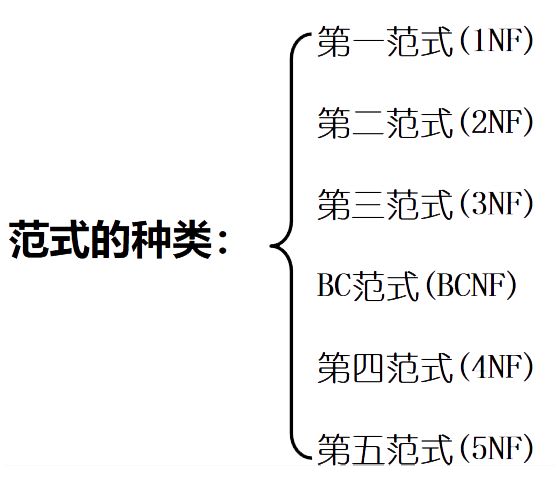
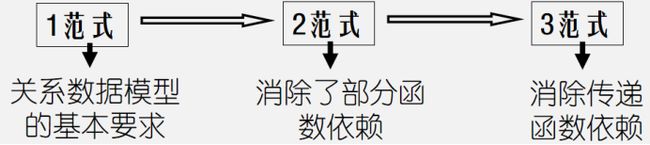
6.2.3范式
√范式：符合某一种级别的关系模式的集合。
√关系数据库中的关系是要满足一定要求的，满足不同程度要求的为不同范式。（个人理解：说到底，范式就是一种标准级别）
√各种范式之间存在联系
√某一关系模式R为第n范式，可简记为R∈nNF。
√一个低一级范式的关系模式，通过模式分解可以转换为若干个高一级范式的关系模式的集合，这种过程就叫规范化 。
√1NF:如果一个关系模式 R 的所有属性都是不可分的基本数据项，则 R∈1NF .
6.2.4 2NF
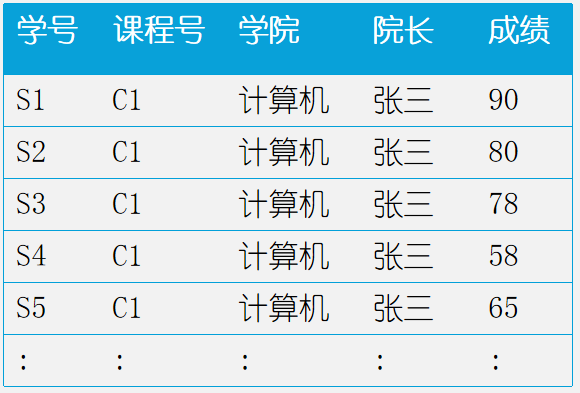
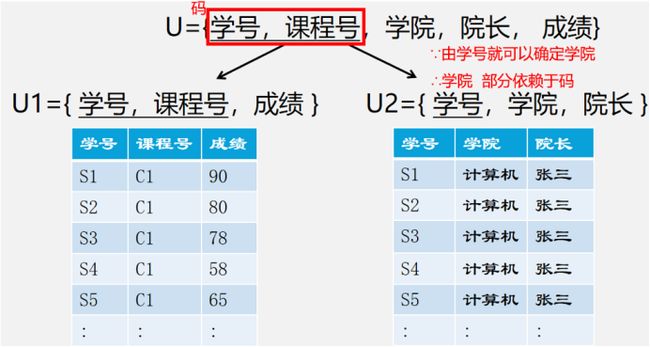
√背景：U={学号，课程号，学院，院长，成绩}
√语义：1）每个学院有若干学生，每个学生只属于一个学院；
- 每个学院只有一名院长；
- 每个学生可以选若干门课，每门课可供若干学生选；
- 每个学生选的每一门课有一个成绩。
如果我们这样设计：（也就是满足1）
| 学号 |
课程号 |
学院 |
院长 |
成绩 |
只要我们随便写点数据进去：
就会存在问题：1、冗余严重 2、更新复杂
3.插入异常：如某个系刚成立没有学生，则系主任的信息无法存入到数据库
4.删除异常:如学生毕业了，要删除学生的信息，则系主任的信息也被删除了
直观上的不合理性：两种不同类的信息混入在一个表中
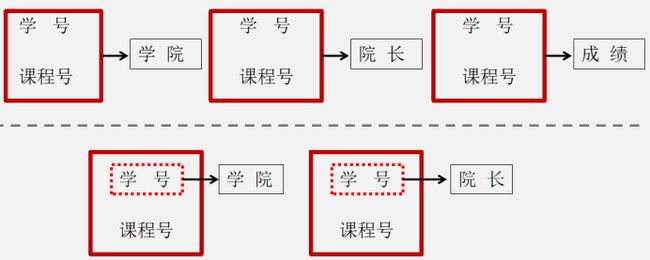
理论上的不合理：存在不合适的函数依赖关系
这个时候我们就要拆分原关系模式，消除存在的部分函数依赖
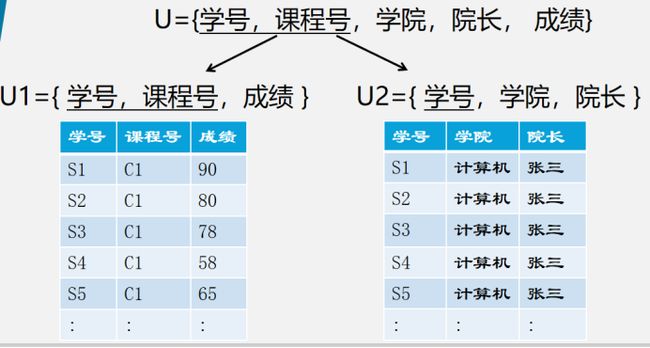
√2NF定义： 如果一个关系模式满足第一范式，并且每一个非主属性都完全函数依赖于码
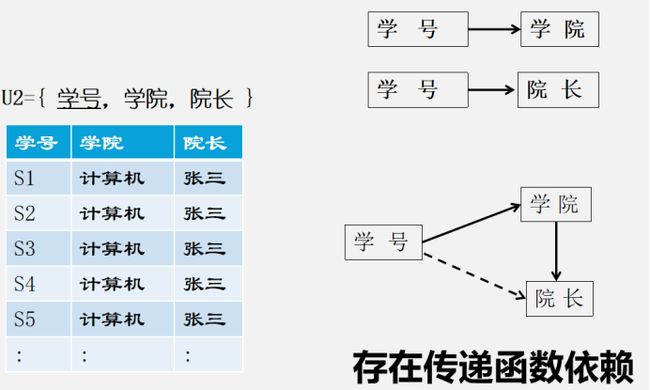
√这个时候我们发现U2表中还是存在一些问题，就需要我们的3NF
6.2.5 3NF（不存在传递函数依赖）
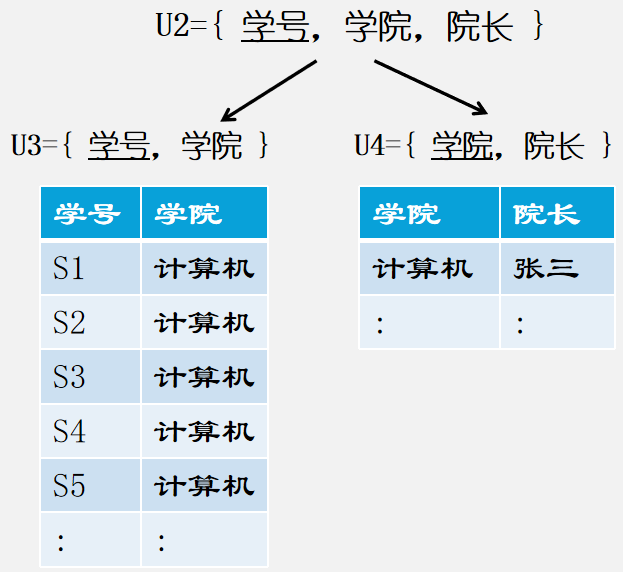
√对上面的U2表再次分解，这样看起来就非常OK了。
√3NF定义：关系模式满足第一范式，并且每一个非主属 性既不部分函数依赖于码，也不传递函数依赖于码.
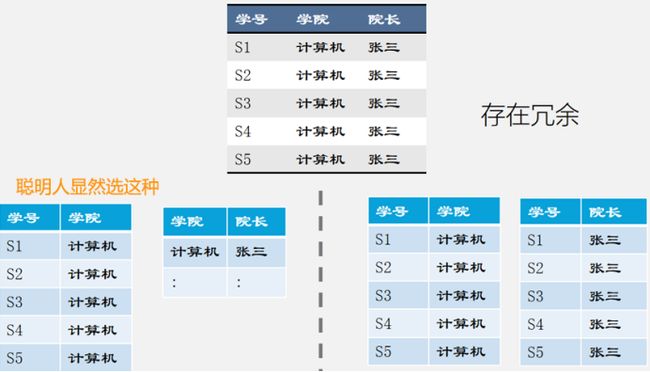
√对上面的分解，其实还有另一种分解法，那么这两种分解法有什么区别呢？
√这种过程，我们成为：规范化。
√规范化的原则：分解前后的等价
√规范化理论是数据库逻辑设计的工具
√目的：尽量消除插入、删除异常，修改复杂，数据冗余
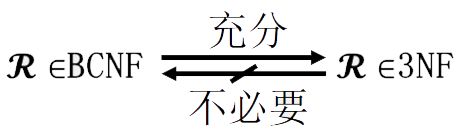
6.2.6 BCNF
BCNF的三个条件：若R∈BCNF
①所有非主属性对每一个码都是完全依赖函数。
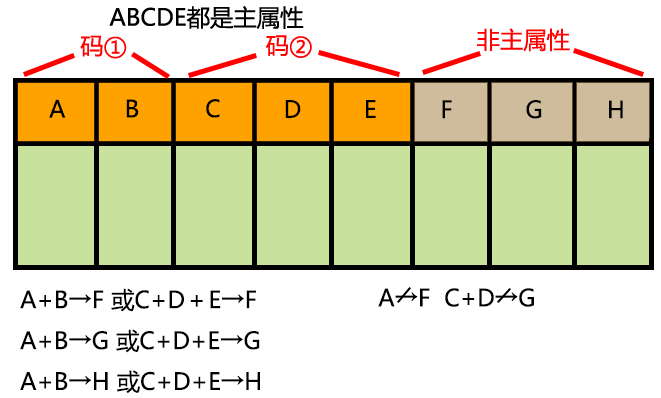
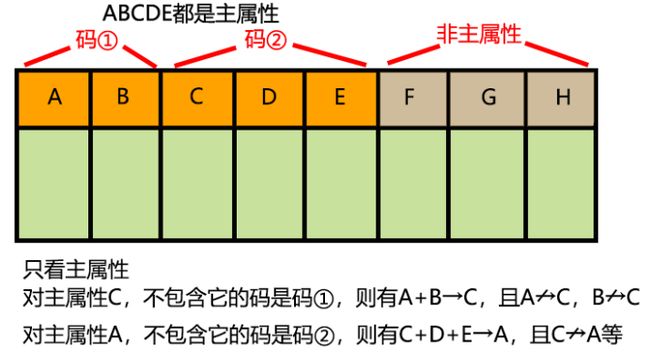
②所有的主属性对每一个不包含它的码，也是完全依赖函数。
③没有任何属性完全函数依赖于非码属性的任何一组属性。
以下是自己对三范式以及BCNF的理解（如果为了理解，建议直接看这里）
①1NF：讲究的是不能再分
②2NF：讲究的是每个非主属性（学院、院长、成绩）都得在每个主属性（学号、课程号）都确定之后才能确定。
比如 学号+课程号→成绩，而对于学院与院长，存在 学号→学院，学号→院长，不符合。
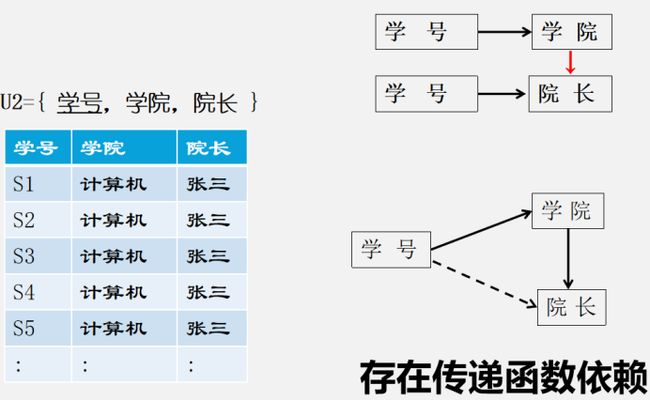
③3NF：不能有传递函数依赖。
比如下图，就存在着传递函数依赖，所以要继续分为表U3={学号，学院}，U4={学院，院长}
④BCNF：我们解读它的三个条件。
1.所有非主属性对每一个码都是完全依赖函数。
2.所有的主属性对每一个不包含它的码，也是完全依赖函数。
3比较简单就不介绍了。
以上是个人理解，接下来就是关于BCNF的例题部分了。
| 例6.5：关系模式 C（Cno，Cname，Pcno） |
|
| ∵它只有一个码Cno ∴不存在部分依赖或传递依赖 ∴C∈3NF 又∵Cno是唯一的决定因素 ∴C∈BCNF |
|
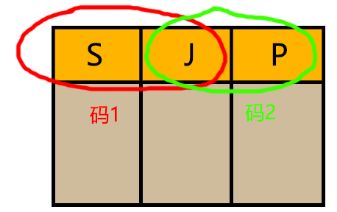
| 例6.7：关系模式SJP（S，J，P），S学生，J课程，P名次。学生选修课程有一定名次，不存在并列的排名 |
|
| ∵（S，J）→P，（J，P）→S ∴（S，J）与（J，P）都是候选码 ∵显然部分依赖与传递依赖 ∴SJP∈3NF 又∵除了（S，J）与（J，P）没有其他决定因素 ∴SJP∈BCNF |
|
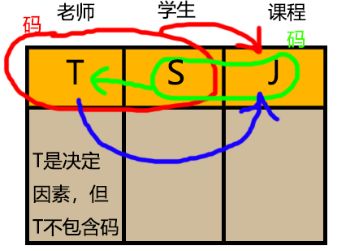
| 例6.8：在关系模式 STC（S，T，C）中，S表示学生，T表示教师，C表示课程。每个教师只教一门课，每门课有若干个老师，某学生选定某门课就对应一个固定的老师。 |
|
| ∵（S，J）→T，（S，T）→J，T→J ∴（S，J）与（S，T）是候选码 ∵不存在传递依赖 所以STC∈3NF 又∵T是决定因素，但T不包含码 ∴STC∉BCNF |
|
6.2.9规划范小结
①关系数据库的规范化理论是数据库逻辑设计的工具
②目的：尽量消除插入、删除异常，修改复杂，数据冗余
③基本思想：逐步消除数据依赖中不合适的部分
④实质：概念的单一化
6.3数据依赖的公理系统
个人理解：就好像F是一个函数映射集。X→Y是其中一个映射。
Armstrong公理系统
| 自反律证明 设t、s是R ∵t[X]=s[X] 又∵Y∈X ∴t[Y]=s[Y] |
| 增广律证明 设t、s是R ∵t[XZ]=s[XZ]，则t[X]=s[X],t[Z]=s[Z] 又∵X→Y ∴t[Y]=s[Y] ∴t[YZ]=s[YZ] |
| 传递律证明 设t、s是R ∵t[X]=s[X] 又X→Y ∴t[Y]=s[Y] 又Y→Z ∴t[Z]=s[Z] |
导出规则
引理6.1
个人理解：闭包就是一个函数依赖的大集合。（有许多写不完函数依赖）
引理6.2
个人理解：如果X→Y能够根据Armstrong公理推出来，那么X→Y这个依赖在
里。
√求闭包的算法
定义6.14：如果
，就说函数依赖集F覆盖G（F是G的覆盖，或G是F的覆盖），或F与G等价。
√证明：
的充分必要条件是
定义6.15：如果函数依赖集F满足下列条件，则称F为一个极小函数依赖集，亦称为最小依赖集或最小覆盖。
①F中任一函数依赖的右部仅含有一个属性。（个人理解：如果有X→AB，则要拆为X→A，X→B）
②F中不存在这样的函数依赖X→A，使得F与F－{X→A}等价。（个人理解：比如X为B，则B→A，但是F中同时又有B→C，C→A，此时B→A就显得多余了，有种传递函数依赖的感觉）
③F中不存在这样的函数依赖X→A，X有真子集Z使得F－{X→A}∪{Z→A}与F等价。（个人理解：比如X为BC，则BC→A，但是F中同时又有B→A，C→A，则BC→A就多余了，有种部分函数依赖的感觉）
定理6.3：每一个函数依赖集F均等价于一个极小函数依赖集
。此
称为F的最小依赖集。（证明：找出F的最小依赖集）
极小化过程
6.4模式的分解
（虽然这一章打了*号，不过老师还是抽了点重点讲了一下）
√分解的等价定义
①无损连接性——分解后能否恢复→分解后的数据表可以通过自然连接恢复
②保持函数依赖——分解前后的语义是否一致
③既保持函数依赖又具有无损连接性
√保持函数依赖的分解
√关于模式分解的几个重要事实：
1）若分解要求保持函数依赖，总可以达到3NF，不一定能到BNCF;
2）若分解既保持函数依赖，又具有无损连接，可以到3NF，不一定到BNCF;
3）若分解只要求具有无损连接，一定可以达到4NF.
√模式分解总结与思考
①分解无损连接性能够保证不丢失信息
②分解保持函数依赖可以减轻或解决各种异常情况
③分解具有无损连接性和分解保持函数依赖是两个互相独立的标准；
④分解必须是连接无损的，最好是依赖保持。