抓知了（new）

Description

深海龙王和水葫芦娃放了暑假闲的无聊，一天他们路过一棵树，听到树上的知了叫的好欢啊∼
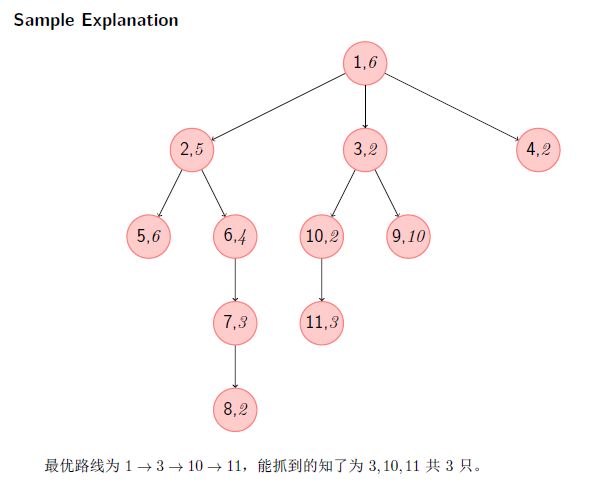
深海龙王准备抓几只知了送给水葫芦娃。他发现面前的这棵树是一颗以1 号节点为根节点的一颗有根树，同时他又发现这颗树上的每一个节点i 上都恰好停有一只蝉，正在愉快的以ai 的响声鸣叫∼
深海龙王会从1 号节点起沿着树边一直爬，直到爬到一个叶子节点（请不要在意他怎么下来），在这途中他可以选择一些他经过的蝉并将它们抓起来。但是水葫芦娃希望深海龙王抓的知了能发出越来越响的鸣叫声，起码得要单调不减！

Input

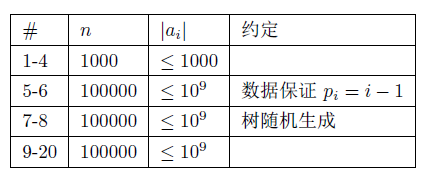
第1 行包含一个整数n，表示树上的结点个数;
第2 行包含n − 1 个整数，分别代表第2 至n 号节点的父亲节点编号；
第3 行包含n 个整数ai，代表i 号节点知了的响声。

Output

一行一个整数，表示深海龙王最多能抓到的知了数。

分析

本来是nlogn的最长不下降子序列的。这种方法在我之前讲过：
http://blog.csdn.net/xieguofu2014/article/details/50034949
现在我要讲的是新的方法——主席树，主席树大法好！
这里我们不用去用二分和辅助数组d来求合法的最大值，对于这点的值为x，我们只需要求ans=区间【1..x】里面的最大的答案，然后这个点的答案就是ans+1.而再放到主席树里面更新最大值就可以了。
在此有读者可能要问了：可不可以用线段树呢？其实是不可以的，因为我们每次往下遍历，在遍历的途中在加上答案，更新线段树。而更新完后我们还要修改回去，这样不好修改。
而主席树就很好的补了这个缺陷，很好的解决这个问题——每颗主席树都是独立的，所以我们就不用像回溯那样修改回去了，只用更新就可以了。
这里是用到主席树的求最大值，不像上几篇文章里面写的是直接计数。

代码

#include
#include
#include
#include
#include
#include
using namespace std;
const int N=100005;
struct node{
    int a,b;
}val[N];
int nu,n,las[N],x,len,b[N],nex[N],t[N*30],root[N*30],cal[N],ans,lef[N*30],rig[N*30],tot;
void insert(int x,int y){
    b[++nu]=y;nex[nu]=las[x];las[x]=nu;
}
void change(int &x,int l,int r,int y,int z){
    lef[++len]=lef[x];
    rig[len]=rig[x];
    t[len]=max(t[x],z);x=len;
    if (l==r) return;
    int mid=(l+r)>>1;
    if (mid1,r,y,z);
    else change(lef[x],l,mid,y,z);
}
int find(int v,int l,int r,int x,int y){
    if (!v)return 0;
    if (l==x&&r==y) return t[v];
    int mid=(l+r)>>1;
    if (mid>=y) return find(lef[v],l,mid,x,y);
    else if (midreturn find(rig[v],mid+1,r,x,y);
    else return max(find(lef[v],l,mid,x,mid),find(rig[v],mid+1,r,mid+1,y));
}
void dfs(int x,int y){
    int z;
    z=find(root[y],1,tot,1,cal[x])+1;
    ans=max(ans,z);
    change(root[x]=root[y],1,tot,cal[x],z);
    for(int p=las[x];p;p=nex[p]) 
    dfs(b[p],x);
}
bool cmp(node x,node y){
    return x.aint main(){
    freopen("cicada.in","r",stdin);
    freopen("cicada.out","w",stdout);
    scanf("%d",&n);
    for(int i=2;i<=n;i++) {
        scanf("%d",&x);
        insert(x,i);
    }
    for(int i=1;i<=n;i++)scanf("%d",&val[i].a),val[i].b=i;
    sort(val+1,val+n+1,cmp);
    val[0].a=-2000000000;tot=0;
    for(int i=1;i<=n;i++){
        if (val[i].a!=val[i-1].a) ++tot;
        cal[val[i].b]=tot;
    }
    dfs(1,0);
    printf("%d",ans);
}