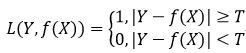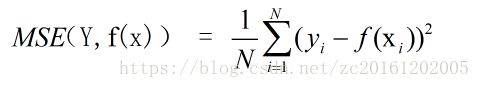机器学习中的损失函数与正则化

        正则化是结构风险最小化的实现策略，形式是在经验风险最小化的后面加上正则项。（正则项一般是模型复杂度的单调递增函数，模型越复杂，正则项的值越大）。

                                                 

损失函数一般有一下几种：

1.  0-1损失函数（感知机）

                                                              

但一般情况下绝对相等比较困难，因此一般设定一个阈值，满足一定条件时即认为相等。

                                                             、

2.  绝对值损失函数

                                                                     

3.  对数损失函数（逻辑回归）

                                                                  

        对数损失函数的有一个前提假设：即样本服从伯努利分布

4.  平方损失函数（回归问题）

        回归的问题转化为了凸优化的问题。最小二乘法的基本原则是：最优拟合曲线应该使得所有点到回归直线的距离和最小。通常用欧式距离进行距离的度量。平方损失的损失函数为：

                                                                                     

5.  指数损失函数（Adaboost）

                                                                                          

6.  Hinge损失函数（主用于最大间隔分类，SVM）

                                                                                             

 一般机器学习任务有分类问题与回归问题，二者的损失函数不相同。

       分类问题中模型输出经过softmax输出结果为预测概率，而回归问题得到的结果为预测数值。

•        分类问题的损失函数为：交叉熵损失函数，其表达式为：

                                                                                

        假设有一个六分类问题，某个样本正确的答案为[0,0,0,1,0,0]，模型经过 softmax 后获得的预测概率为[0,0.1,0.2,0.3,0.2,0.2].那么这个预测和正确答案之间的交叉熵为：H（[0,0,0,1,0,0]，[0,0.1,0.2,0.3,0.2,0.2])= - ( 0*log 0 + 0*log 0.1 + 0*log 0.2 + 1*log 0.3 + 0*log(0.2) + 0*log(0.2) ) ≈ 0.5229.

        若获得的预测概率为[0,0.1,0,0.85,0.02,0.03]，那么这个预测和正确答案之间的交叉熵为：H（[0,0,0,1,0,0]，[0,0.1,0,0.85,0.02,0.03])= - ( 0*log 0 + 0*log 0.1 + 0*log 0+ 1*log 0.85 + 0*log(0.02) + 0*log(0.03) ) ≈ 0.0706.

从预测概率上来看，第二个模型的预测结果比第一个模型预测结果要好，而且交叉熵比第一个模型的小。因此可以说第二个模型比第一个模型更优。

     

•      对于回归问题来说，损失函数定义为均方误差：

                                                

过拟合与欠拟合： 

• 过拟合：

        模型过于复杂或者没有足够的数据支持模型的训练时，模型含有训练集的特有信息，对训练集过于依赖，即模型会对训练集高度敏感，这种现象称之为模型过拟合。对于同一个模型，更换训练集，同一个测试集对不同训练集的的预测结果会产生较大偏置，且各个预测结果较为分散，产生较高方差。（这也是高方差的原因）

• 欠拟合：

        模型不够复杂或者训练数据过少时，模型均无法捕捉训练数据的基本(或者内在)关系，会出现偏差。这样一来，模型一直会错误地预测数据，从而导致准确率降低。这种现象称之为模型欠拟合。对于同一个模型，更换训练集，都不能很好的拟合训练集数据，同一个测试集针对不同训练集的预测结果较为集中，但是与真实标签偏差很大，形成较高偏差。（高偏差）

正则化：

   说到正则化需要先知道为什么要引入正则化？

          模型训练过程中，往往为了追求损失函数最小化会导致模型复杂度过高，这样生成的模型泛化能力不好，训练集的准确率较高，而验证集的准确率较低，形成过拟合现象。为了避免这种情况发生，减小模型复杂度的同时，使损失函数尽量降低，在经验风险后面添加了惩罚函数，也就是所谓的正则项。

          一般常使用的正则化技术包括：L1正则化与L2正则化。

• L1正则化：求取正则向量（例如权值向量）中各个元素的绝对值之和。表示为：                                                                                                                                  
• L2正则化：求取正则向量的模，即求取各元素平方和的开平方。表示为：

                                                       

其中L1正则化可以产生稀疏权值矩阵，构建稀疏模型，可以用于特征筛选，在一定程度上可以防止过拟合；L2正则化则可以防止模型过拟合。

对于L1正则化，L2正则化，个人觉得（正则化项L1和L2的直观理解）讲的较为详细，本文正则化部分以此作为参考。