跟我学神经网络3-卷积神经网络
文章目录
- 1. 关键词
- 2. 引言
- 3. 结构
- 4. 卷积
- 4.1 核函数
- 4.2 填充
- 5. 线性整流
- 6. 池化
- 7. 降维采样
- 8. 例子
- 9. 附录
- 9.1 中英文对照表
- 9.2 扩展阅读
![]()
欢迎关注《汽车软件技术》公众号,回复关键字获取资料。
1. 关键词
卷积,ReLU,池化,PyTorch,Google Colab
2. 引言
前两章已经学习率基本的神经网络及其求解方法,但神经网络从研究走向实用,还需要进一步演化。以图像识别为例,每个像素作为一个神经元,需要计算非常多的权重,是不现实的。
3. 结构
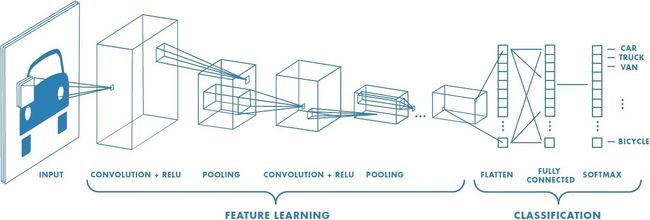
卷积神经网络同样来自生物学,动物视觉皮层只响应一部分覆盖范围内的周围单元(接受域),提高了效率。下图是一个典型结构:
包含了:
- 卷积(Convolution)层
- 线性整流(ReLU)层
- 池化层(Pooling)
- 全连接(Fully connected)层
下面分别介绍。
4. 卷积
卷积是为提取区域内特征进行的一种运算,公式如下:
S ( i , j ) = ( I ∗ K ) ( i , j ) = ∑ m ∑ n I ( i + m , j + n ) K ( m , n ) S(i,j)=(I*K)(i,j)=\sum_m\sum_nI(i+m,j+n)K(m,n) S(i,j)=(I∗K)(i,j)=m∑n∑I(i+m,j+n)K(m,n)
其中:
- I I I 是输入;
- K K K 是核函数;
- S S S 是特征映射。
- i , j i,j i,j 是输出的索引;
- m , n m,n m,n 是核函数索引。
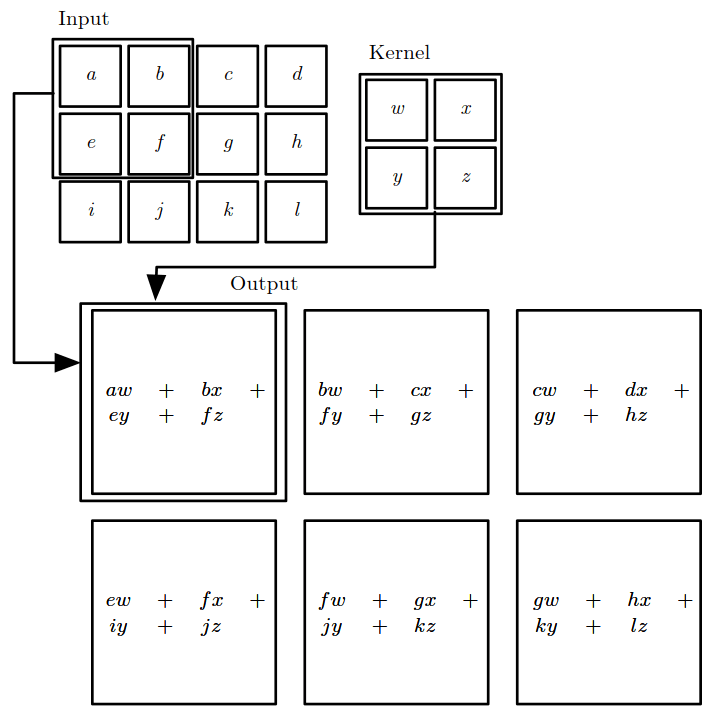
假设输入3x4,卷积核2x2,步幅是1,得到输出2x3,见下图,其中 S 0 , 0 = ∑ m = 0 1 ∑ n = 0 1 I ( 0 + m , 0 + n ) K ( m , n ) = a w + b x + e y + f z S_{0,0}=\sum\limits_{m=0}^1\sum\limits_{n=0}^1I(0+m,0+n)K(m,n)=aw+bx+ey+fz S0,0=m=0∑1n=0∑1I(0+m,0+n)K(m,n)=aw+bx+ey+fz。步幅指的是区域平移的间隔。
卷积与全连接神经网络对比,有以下特点:
- 稀疏交互:输出单元只和一部分输入单元关联;
- 参数共享:卷积核中的每个参数都重复使用;
- 等变表示:将输入或卷积核经过平移、旋转等操作,不会影响最终的输出结果,特征不变。
基于上述特征,卷积网络权重数量明显减少。
以此网络做对比:
| 对比 | 卷积网络 | 全连接网络 |
|---|---|---|
| 权重数量 | 2x2=4 | (3x4)x(2x3)=72 |
对比不同图像的卷积计算:
| 图像 | 例子 | 层数 |
|---|---|---|
| 灰度 | 手写字识别 | 1 |
| 彩色 | RGB | 3 |
4.1 核函数
通常根据经验选取,例如图像处理的边缘检测,可以使用如下的核:
处理效果如下:
当输入是多维的,比如彩色RGB图像,深度是3,卷积核也对应深度是3。
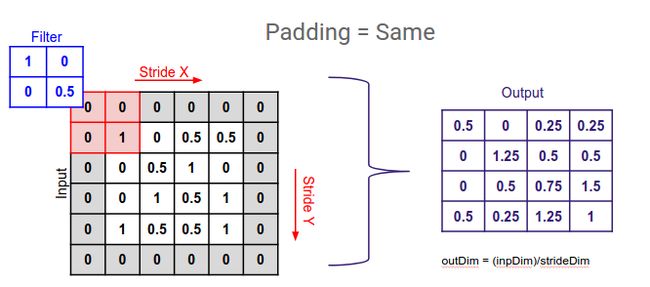
4.2 填充
使用卷积计算后,输出比输入维度减小,有时为了保持相同的维度,需要在输入填充0。如下图所示,填充后,维输入和输出维度相同。
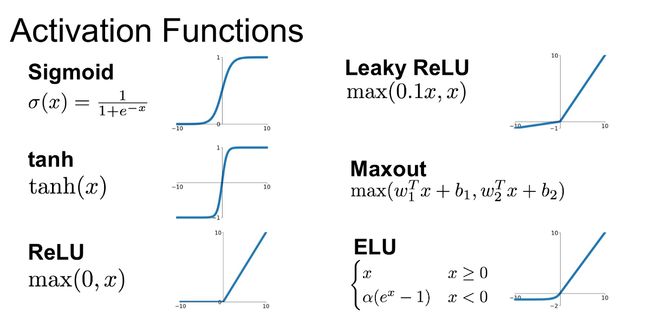
5. 线性整流
之前已经介绍过 sigmod 函数,当前机器学习领域主要应用 ReLU 函数。
f ( x ) = x + = max ( 0 , x ) f(x)=x^+=\max(0,x) f(x)=x+=max(0,x)
ReLU 梯度: x < = 0 , f ′ = 0 ; x > 0 , f ′ = 1 x<=0,f'=0;x>0,f'=1 x<=0,f′=0;x>0,f′=1。ReLU 在0点不可导,一般按0处理。
6. 池化
使用多个核进行卷积计算,得到一组输出,对输出采样时使用的方法称为池化。一般使用2x2最大池化,保留特征值。下图是最大池化,步幅是2。
![]()
7. 降维采样
输入经过卷积或池化后,输入和输出的维度关系如下:
W o u t = W i n − F + 2 P S + 1 W_{out}=\frac{W_{in}-F+2P}{S}+1 Wout=SWin−F+2P+1
其中:
- W i n W_{in} Win 是输入维度;
- F F F 是卷积核或池化维度;
- P P P 是填充维度;
- S S S 是步幅;
- W o u t W_{out} Wout 是输出维度。
8. 例子
本文基于 CIFAR10 数据集,使用 PyTorch 实现一个图像识别例子,PyTorch 是当下最流行的人工智能库,参考 PyTorch 文档。
按照以下步骤:
- 使用
torchvision加载和正则化的 CIFAR10 数据集; - 定义一个卷积神经网络;
- 定义一个损失函数;
- 使用训练数据集进行训练;
- 使用测试数据集进行测试。
代码部署在 Google Colab,使用 Google 服务器进行计算,提供了 GPU/TPU 加速。
后续完善卷积层和池化层的反向传播算法。
9. 附录
9.1 中英文对照表
| 英文 | 中文 | 缩写 | 数学符号 |
|---|---|---|---|
| Convolution | 卷积 | s ( t ) = ( x ∗ w ) ( t ) s(t)=(x*w)(t) s(t)=(x∗w)(t) | |
| Convolutional Neural Network | 卷积神经网络 | CNN | |
| Equivariant Representations | 等变表示 | ||
| Feature Map | 特征映射 | ||
| Kernel | 核 | w w w | |
| Max Pooling | 最大池化 | ||
| Padding | 填充 | ||
| Parameter Sharing | 参数共享 | ||
| Pooring | 池化 | ||
| Receptive Field | 接受域 | ||
| Sparse Interactions | 稀疏交互 | ||
| Stride | 步幅 |
9.2 扩展阅读
- 维基百科
- 图像处理常用卷积核