模型学习全面概述:利用机器学习查找软件漏洞
选自ACM
作者:Frits Vaandrager
机器之心编译
Communications of the ACM 近日发表一篇题为《Model Learning》的文章,详细介绍了模型学习及其研究现状和应用。
本文的要点是:
模型学习的目标是通过提供输入和观察输出来构建软件和硬件系统的黑箱状态图模型(black box state diagram model)。模型学习的算法的设计师一个基本的研究问题。
模型学习正在成为一种高效的漏洞寻找技术,有银行卡、网络协议和遗产软件等领域的应用。
在新算法的设计上,最新出现了很多新进展,既有有限状态图(Mealy 机)背景的进展,也有数据(register automata)背景的进展。通过抽象(abstraction)技术的使用,这些算法可以被应用到复杂系统上。
按下按键观察结果,这是我们学习一个装置或计算机程序的惯常做法。孩童尤其擅长这一点,无需借助手册他们便可以搞懂如何正确使用智能手机或微波炉。鉴于以上,我们建构了一个心智模型——一个装置状态图:做一些实验,即可获知该装置的整体状态以及输入所对应的状态转换与输出结果。本文介绍了自动执行此任务的算法的设计与应用。
有很多推断软件组件模型的方法,比如分析代码、挖掘系统日志、执行测试;有不同的模型被推断过,比如隐马尔可夫模型、变量之间的关系、类图(class diagrams)。在本文中,我们关注一种特定类型的模型,即状态图(state diagrams),其对于理解许多软件系统的行为至关重要,例如(安全和网络)协议和嵌入式控制软件。模型推断技术分为白箱和黑箱,区别在于是否需要访问代码。本文只讨论黑箱技术。这些技术的优点是相对容易使用,并可以应用在我们没有代码访问权限或足够的白箱工具的情况下。作为最终的限制,我们只考虑主动学习(active learning)的技术,即通过主动地对软件进行实验(测试)来完成它们的任务的技术。此外,还有一个广泛的被动学习(passive learning)工作,其中模型是从(一组组)运行的软件构建的。主动学习的优点是它提供了软件组件的完整行为模型,而不仅仅是在实际操作期间发生的特定运行的模型。
状态图(或自动机(automaton))的主动性黑箱学习的基本问题的研究已经持续了几十年。1956 年,Moore 首先提出了学习有限自动机(finite automata)的问题,并提供了一个指数算法,还证明这个问题本质上是指数式的。后来,不同的组织以不同的名字对这个问题进行着研究:控制论学家把它称为「系统辨识(system identification)」;计算语言学家称之为「语法推理(grammatical inference)」;一些论文将其命名为「常规推理(regular inference)」、「常规外推(regular extrapolation)」、「主动性自动机学习(active automata learning)」;安全研究者造了个新术语「协议状态模糊(protocol state fuzzing)」。本文中,我们使用的术语「模型学习(model learning)」与经常使用的「机器检查(model checking)」类似。虽然「模型检查」被广泛用于分析有限状态模型,但「模型学习」则是通过观察输入-输出数据以构建模型的补充技术。
1987 年,Angluin 发表了一篇研讨论文,她表明可以使用所谓的会员查询(membership query)和等价查询(equivalence queries)来学习到有限自动机。自此之后,尽管提出了更快算法,但最有效的学习算法依然遵循着 Angluin 所提出的 MAT(minimally adequate teacher/最低限度足够的教师)的原则。在 MAT 框架中,学习被看作是一个博弈(game),其中学习器(learner)必须通过询问教师(teacher)来推断一个未知的状态图的行为。在我们的设定中,教师知道状态图,其被称为 Mealy 机(Mealy machine),简称:M。一开始,学习器只知道 M 的输入 I 和输出 O。学习器的任务是通过两种类型的查询学习 M:
使用会员查询 (MQ/membership query):学习器询问输入序列σ ∈ I*对应的输出结果是什么。教师使用输出序列 AM(σ) 来回答。
使用等价查询 (EQ/equivalence query):学习器询问一个带有输入 I 和输出 O 的虚拟的 Mealy 机 H 是否正确,即:H 和 M 是否等同。如果情况属实,教师回答「是」。否则教师回答「否」,并提供一个反例σ ∈ I*来区分 H 和 M。
Angluin 的 L*算法能够通过询问会员查询和等价查询的多项式数(多项式数的大小对应于典型的 Mealy 机)来学习 Mealy 机 M。在 Angluin 的算法中我们给 L*做了一个简化,实际的实现中(例如 LearnLib 和 libalf)则包含很多优化。
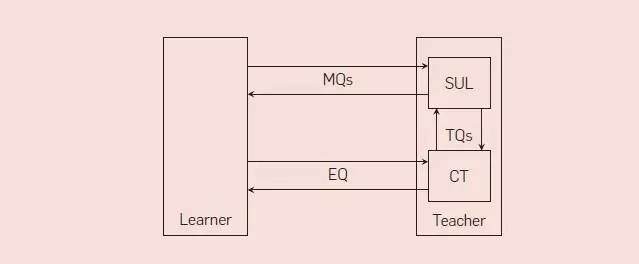
Peled 等人作出了重大发现:MAT 框架可以用来学习软硬件组件的黑箱模型。假设我们有一个组件,我们称之为系统学习(SUL),其行为可以由(未知的)Mealy 机 M 描述。我们进一步假设,总是可以使 SUL 回到其初始状态。现在,通过使 SUL 回到初始状态并进一步观察给到 SUL 的输入序列所对应的输出结果可以实现会员查询。等价查询可以通过有限数量的测试查询(TQ/test queries)以使用一致性测试(CT/conformance testing)工具来接近。测试查询询问 SUL 对输入序列的响应,类似于会员查询。如果其中一个测试查询呈现反例,则等价查询的答案为否,否则答案为是。示意图如图 4 所示。在这种方法中,学习者的任务是构造假设,而一致性测试工具的任务是测试这些假设的有效性。由于测试工具只能构造有限数量的查询,因此我们无法确定一个学习模型的正确性。然而,如果我们假定机器 M 的状态数量有界限,则存在有限和完整的一致性测试套件。
图.4
Peled 等人和 Steffen 等人的开创性工作在模型学习和正式方法的领域之间建立了迷人的联系,特别是模型检验和基于模型的测试。随后的研究已经证实,在没有反应系统的易处理的白箱模型的情况下,学习模型通常是可以以相对低的成本获得的优良的替代方案。
为了检查学习模型的属性,可以使用模型检查(model checking)。事实上,Peled 等人已经在一种叫「黑箱检查(black box checking)」的方法中展示了如何完全整合模型学习与模型检查,其基本思想是使用模型检查器作为图 4 中一致性测试工具的「预处理器(preprocessor)」。当教师接收到学习器的假设时,首先运行模型检查器以验证假设模型是否满足 SUL 规定的所有属性。只有假设为真时,才转发给一致性测试器(conformance tester)。如果其中一个 SUL 属性不成立,那么模型检查器产生一个反例。现在有两种情况。第一种可能性是反例可以在 SUL 上再现。这意味着我们已经在 SUL(或其规定中)中展示了一个错误,我们停止学习。第二种可能性是反例不能在 SUL 上再现。在这种情况下,教师遵循假设是不正确的原则向学习器返回反例。在后来的工作中,黑箱检查方法已经进一步完善,并已成功应用于几个工业案例。
大多数学习算法的所需会员查询数量随着输入数量线性增长,并与状态数量成二次方。这意味着当输入数量增长时,学习算法规模相当好;换句话说,制定一个新的假设是容易的。然而,检查假设是否正确(一致性测试)会很快成为大量输入的瓶颈。如果当前假设具有 n 个状态,则 SUL 具有 n' 个状态,并且存在 k 个输入,则在最坏的情况下,需要运行包含 n'-n 个输入的所有可能序列的测试序列,即 k(n' − n) 个可能性。因此,模型学习目前只能应用于少于 100 个输入的情况下。因此,我们寻求帮助我们减少输入数量的方法。
抽象(abstraction)是将模型学习方法扩展到现实应用程序的关键。Cho 等人通过在僵尸网络服务器和学习软件之间放置仿真器/映射器(emulator/mapper),将字母符号具体化为有效的网络消息并将它们发送到僵尸网络服务器(botnet servers),成功推断出现实僵尸网络命令和控制协议的模型。当接收到响应时,仿真器作反向处理:它将响应消息抽象为输出的字母,并将它们传递到学习软件。这种学习设置的示意图概述如图 5 所示。处理抽象的中间映射器组件的想法是非常自然的,并且在许多关于自动机学习的案例研究中被隐含地或明确地使用。Aarts 等人通过与谓词抽象(predicate abstraction)和抽象解释(abstract interpretation)建立连接,发展出了关于中间性抽象(intermediate abstraction)的数学理论。
图.5
一个补充性的简单但实用的方法是将模型学习应用在多个更小的输入子集上。这将明显降低学习复杂性;还因为对于有限数量的刺激,可达状态的集合通常将更小。然后,对于输入的子集学习的模型可以用于在学习更大子集的模型时生成反例。例如,Chalupar 等人已经应用的另一种方法是将通常以特定顺序发生的多个输入动作合并成单个高级动作,从而减少输入的数量。再次,已经用少量高级输入学习的模型可以用于在后续实验中产生反例,其中这些输入被分解成它们的组成部分。
正如 C.A.R. Hoare 所说,一个人可以说,在每个大程序中都有一个小的状态机试图出去。通过选择适当的输入动作集合并定义适当的映射器/抽象,我们可以使这个小状态机对学习者可见。
应用案例
近年来,模型学习已经成功应用于不同领域的许多实际案例。工业应用的例子有,例如,在西门子的电信系统的回归测试(regression testing),在法国电信的集成测试,在施普林格出版社线上会议的自动测试,在沃尔沃科技的线控制动系统的测试要求。下面,我将概述奈梅亨大学(Radboud University)在智能卡、网络协议和遗产软件(legacy software)方面进行的一些代表性案例研究。
智能卡。Chalupar 等人使用模型学习来反向工程 e.dentifier2——一种用于网上银行的智能卡阅读器。为了能够学习 e.dentifier2 的模型,作者构建了一个由树莓派(Raspberry Pi)控制的乐高机器人,可以操作读取器的键盘(参见图 6)。从笔记本电脑控制所有这些之后,他们可以使用 LearnLib 学习 e.dentifier2 的模型。他们学习了一个版本的 e.dentifier2 的四态 Mealy 机,揭示了存在的一个安全缺陷,并且表明该缺陷不再存在于新版本设备的三态模型中。
图.6
在另一项研究中,Aarts 等人学习了银行卡上的 EMV 协议套件的实现模型,这些银行卡有来自几家荷兰和德国银行的,有荷兰和瑞典银行发行的万事达信用卡以及一张英国签证借记卡。为了学习模型,LearnLib 对每个卡执行 855 到 1696 个会员和测试查询,并生成 4 到 8 个状态的模型。(图 7 展示了其中一个学习的模型)。所有卡产生不同的模型,只有荷兰银行卡上的应用程序是相同的。所学到的模型没有揭示任何安全问题,虽然注意到一些怪异问题。作者认为,模型学习将作为安全评估的一部分发挥作用。
图.7
网络协议。我们的社会已完全依赖于网络和安全协议的正确运作;这些协议中的错误或漏洞可能会导致安全漏洞甚至是彻底的网络故障。模型检查已被证明是一种用于发现此类错误与漏洞的有效技术。然而,由于针对协议实现的详尽模型检查通常不可行,因此模型检查通常会应用于根据协议标准开始人工制作的模型。这意味着由于协议实现不符合模型检查的规范,其出现的错误便无法被捕捉。研究证明,模型学习能够有效地找到此类错误,使这项技术得以与模型检查互补。
例如,De Ruiter 和 Poll 使用支持多种密钥交换算法和客户端认证选项的测试工具分析了 TLS 协议的服务器端和客户端实现。结果表明模型学习(或称为协议状态模糊)可以捕获一类有趣的实现缺陷,而这种缺陷在安全协议实现中十分常见:在九个受测试的 TLS 实现中,有三个能够发现新的安全缺陷。如 Java Secure Socket Extension 便是一类学习了 Java 1.8.0.25 版本的模型。他们发现该模型包含两条通往应用程序数据交换的路径:常规 TLS 协议运行和另一意外运行。客户端以及服务器应用程序都以为它们处于安全的连接上交谈,但实际上任何人都能够通过利用这种行为读取并篡改客户端的数据。所以修复作为安全更新的一个关键部分而被发布,并且他们能够通过学习 JSSE 1.8.0.31 版本的模型来确认问题是否已解决。得益于人工构建的抽象/映射器,经验丰富的 Mealy 机包含 6 至 16 个状态并且规模都很小。另外,由于对不同的 TLS 实现的分析产生了独一无二的 Mealy 机,模型学习也可用于为 TLS 实现添加指纹印记。
Fiterau 等人在一个涉及 Linux、Windows 以及使用 TCP 服务器与客户端的 FreeBSD 实现的案例研究中将模型学习与模型检查进行了结合。模型学习用于推断不同组件的模型,而后应用模型检查来充分探索当这些组件(如 Linux 客户端和 Windows 服务器)交互时可能的情况。案例研究揭示了 TCP 实现中不符合其 RFC 规范的几个例子,具体示例参见图 8。
图.8
遗产软件(Legacy software)。遗产系统被定义为「不知如何处理却对组织至关重要的大型软件系统」(7)。通常这些系统的技术已经过时,并且文档存在限制,原始开发人员也已经离职。此外现有的回归测试将受限。鉴于以上特征,需要改变传统组件的创新存在风险。故而开发了几种技术用于提取隐藏在传统组件中的关键业务信息,并支持重构实现的结构。Margaria 等人(30)首先指出,模型学习可能有助于确认传统组件和重构实现具有相同的行为。
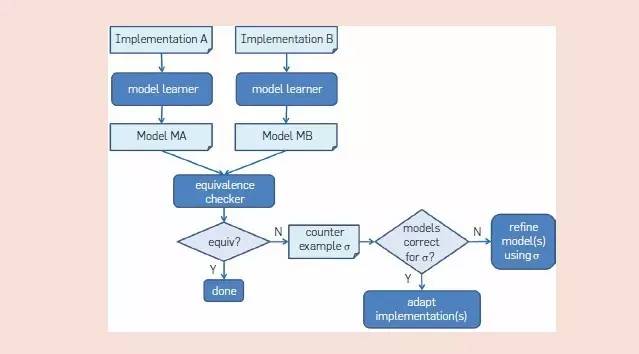
例如 Schuts 等人在飞利浦的开发项目中使用模型学习来支持传统嵌入式软件的复兴。该项目涉及到一个新引入的硬件组件——电源控制组件(PCC),用于启动和关闭介入放射学系统。系统中的所有计算机都具有软件组件,即在启动和关闭的执行期间通过内部控制网络与 PCC 通信的电源控制服务(PCS)。为了处理具有不同接口的 PCC 的新硬件,则需要 PCS 的新型实现。由于必须支持新型和旧型 PCC 硬件的不同配置,新型与旧型 PCS 软件需要具有完全相同的外部行为。图 9 说明了所遵循的方法。由传统的 A 实现以及重构的 B 实现可获得 Mealy 机器模型 MA,而使用模型学习可获得 MB;这些模型将使用等价检查器进行比较。当等价检查器发现反例σ时,我们将检查 A 和 MA 在输入σ上表现是否相同,同样检查 B 和 MB 在输入σ上是否相同。若 A 和 MA 或者 B 和 MB 存在差异,我们便会要求学习者基于反例σ构造一个改进的模型。否则σ便表示 A 和 B 之间的差异,而我们也会根据对于σ的响应表现差劲的行为来改变 A 或 B(或是两者)。为了解决可扩展性问题,往往通过增加刺激来学习以及迭代地检查实现。在组件集成之前的早期阶段,重构实现和传统实现都出现了问题。也正因如此,才能避免开发的后期阶段昂贵的重工现象。
图.9
最新进展
近年来,有关模型学习的算法已取得显著进步,这对将这些技术应用扩展到更大的系统而言至关重要。
基本算法。自 1987 年以来,Angluin's 的 L *算法已得到显着改善。原始 L *对观察表中的每个条目执行成员资格查询;但这通常是多余的,因为该查询的唯一目的是区分状态(行)。因此,Kearns 和 Vazirani 通过鉴别树(discrimination trees)将 L *算法的观察表进行重设,而该鉴别树基本上是用于确定等价状态的决策树。
L *的另一个低效的体现是将反例的所有前缀作为行添加到表格中。通过一致性测试或运行时监控获得的反例样本可能极长且极小,而这会导致大量多余的成员资格查询。Rivest 和 Schapire 发现不必将反例的所有前缀作为行添加到表格中,将一个选定的后缀添加为列便足够了。
Isberner 等人提出的新 TTT 算法是目前用于主动学习的最有效的算法。该算法基于 Kearns 和 Vazirani 以及 Rivest 和 Schapire 的想法,但消除了通过清理内部数据结构及重新组织判别树来处理长型反例时过长的鉴别树。假设某 Mealy 机 M 具有 n 个状态和 k 个输入值,并且返回的最长反例长度为 m。然后在最坏的情况下 TTT 算法需要长度为 O(n + m)的 O(n)个等价查询和 O(kn2 + nlog m)个成员资格查询。这种最坏情况的查询和符号复杂度与 Rivest 和 Schapire 的算法一致,但实践中 TTT 的速度更快。
TTT 算法通常比 L *算法产生更多的中度假设(intermediate hypotheses)。这表明单就 membership 查询中使用的输入符号数量可能并不是比较学习算法的适宜度量:我们还需考虑实现等价查询所需的测试查询的数量。membership 与测试查询中的输入符号的总数似乎是比较实践中学习方法的可靠度量。我的两个学生 J.Merman 和 A.Fedotov 在大量基准(协议、控制软件、回路等)上,比较了学习算法和测试算法的不同组合,并发现 TTT 使用的输入符号平均比 L*少 3.9 倍。
当可以同时运行 SUL 的多个实例时,学习和测试能够很容易被并行化。能够加速学习的另一项技术是保存并恢复 SUL 的软件状态(检查点)。其中的益处是:当 learner 想要从保存的 q 状态中探索不同的外向转换时,仅仅需要恢复 q,这通常比复位系统,再经由输入序列返回到 q 要快得多。Henrix(21)报告了在实验中使用 DMTCP(分布式多线程检查点)进行检查点加速学习,系数为 1.7。
寄存器自动机。尽管我们已经看到学习状态机中基本算法的诸多进步,但这些算法仅能成功学习相对很小的状态机。为了能把这些算法扩展至现实应用领域,使用者一般需要手动构建抽象或者映射器。2这可能是个耗时的活动,需要几次迭代和 SUL 的专业知识。因此,最近已经进行了许多工作以将学习算法推广到结构更多结构、类型更丰富类的模型中去,特别是其中数据值可以被传送,存储和操纵的 EFSM 模型。
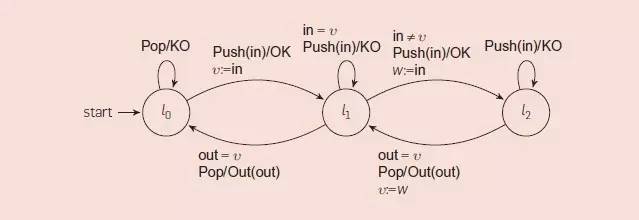
模型学习算法的开发正是对寄存器自动机进行的特定扩展。11 这些自动机具有有限的一组状态,但都用一组可用于存储数据值的寄存器进行扩展了。输入和输出动作被参数化为具体的数据值,可以在转换保护中进行相等测试并存储在寄存器中。图 10 给出了寄存器自动机的简单示例,即容量为 2 的 FIFO 集。一个 FIFO 集对应于一个只能存储不同值的队列。它有一个 Push(d)输入符,用来尝试在队列中插入值 d 的符号,还有一个 Pop 输入符,用来尝试从队列中取回一个值。如果输入值可以成功添加,则 Push 的对应输出为 OK,如果输入值已经在队列中或者队列为满,则 Push 的对应输出为 KO。如果以队列中最旧的值作为参数,则 Pop 的对应输出是 Out,如果队列是空的,则 Pop 的对应输出是 KO。
图.10
抽象是将模型学习方法扩展至现实应用的关键
在寄存器自动机中,所有数据值是完全对称的,且这种对称性是可以在学习过程中被利用的。在本文中已经探索了两种不同的方法。第一种方法,以 Cassel 等人为代表,12 已在软件工具 LearnLib26 和 RALib 中得到实施。10 模型学习算法通常依赖于 Nerode 关系(Nerode relation)来识别已学过的自动机的状态和转换:如果两个词的残差语言(residual languages)吻合,这两个词则导致相同的状态。现在的基本思想是为寄存器自动机设计出一个类似 Nerode 的同余关系,而这决定了已推断的自动机的寄存器的状态、转换、和内容。这种实施方法的技术基础是所谓的符号决策树(symbolic decision trees),它可以用来总结许多用简明符号表达的测试结果。
学习寄存器自动机的第二种方法,以 Aarts 等人为代表,已在软件工具 Tomte 中得到实施。这种方法使用反例引导的抽象提炼来自动构建适当的映射器。这种想法源于一个彻底抽象,即完全忽略在输入和输出动作中出现的数据值。当这种抽象过于粗糙时,learner 将观察到非确定性行为。比如在图 10 的示例中,输入序列 Push Push Pop Pop 大部分情况触发的输出为 OK OK Out KO,但有时为 OK OK Out Out。出现这种行为就需要对抽象进行提炼。在我们的示例中,比如就第二个 Push,我们至少需要两个抽象版本,因为这显然关乎该输入的数据值是否等于第一个 Push 的数据值。RALib 和 Tomte 在性能上都优于 LearnLib。Tomte 和 RALib 的性能大致相当。RALib 在一些基准测试中胜过 Tomte,但是 Tomte 能够学习一些 RALib 无法处理的寄存器自动机,例如容量为 40 的 FIFO 集。
研究挑战
即使模型学习已经在许多地方得到成功应用,但该研究领域仍处于起步阶段。模型学习的应用具有巨大的潜力,尤其是在传统控制软件领域,但是还需要对算法和工具进行更多的研究,以将模型学习从目前的学术原型水平转变为可实际使用的技术水平,从而方便应用于大量不同类型的系统。在这里,我将讨论一些主要的研究挑战。
谓词与数据操作。最近对寄存器自动机模型学习算法所做的扩展是一个突破,这可能使模型学习适用于更大范围的系统。由于不允许对数据进行操作的限制,可以被描述为寄存器自动机的系统类型很少,并且主要由一些学术样例构成,例如有界重传协议和一些简单数据结构等等。然而,如 Cassel 等人所指,12 使用 SMT 解决寄存器自动机的新学习算法可以被扩展为 EFSM 的形式,其中模型防护(guard)可能包含谓词,如 successor 和小于关系(less than relation)。目前已经有 RALib 的原型实现,而且我们正在接近可以自动学习真实世界协议模型的目标,这样的协议可以像 TCP、SIP、SSH 和 TLS 等等,而这些都不需要手动定义抽象。然而,我们对使用不同谓词和操作学习 EFSM 的算法的理解仍然有限,而且还有许多悬而未决的问题。
即使模型学习已经在许多地方得到成功应用,但该研究领域仍处于起步阶段。
Isberner24开发了一种用于可视下推自动机(VPA)的模型学习算法,该算法是 Alur 和 Madhusudan 提出的一种限制类型的下推自动机。5 这个结果在某种意义上与学习寄存器自动机上的结果正交:使用寄存器自动机学习,可以学习具有存储来自无限域的、带有有限容量存储值的堆栈,而使用 VPA 学习可以学习具有无限容量的堆栈,其存储来自有限域的数据值。从实践角度来看,开发一种通用于寄存器自动机和 VPA 这一类模型的学习算法将是有用的。许多协议中的消息可以缓冲,因此我们需要能够学习具有无限容量的队列的算法。
超越 Mealy 机。在 Mealy 机中,单个输入始终触发单个输出。然而,在实践中,系统可以用零个或多个输出来响应输入。此外,系统的行为通常是时序相关的,并且某个输出可能仅在某些输入未能在一定量的时间内得到时才发生。因此,模型学习的实际应用经常严重受限于 Mealy 机缺乏表达性。例如,为了将 TCP 实现为 Mealy 机,我们必须消除基于时序的行为以及重传(retransmissions)。17 已经有一些初步的工作,将学习算法扩展到 I / O 自动机 4和事件记录自动机,18 但是仍然需要大量的工作将这些想法变成实际的工具。
由于一个输入序列可能导致在不同运行中会有不同的输出事件,因此从这种意义上来说,系统通常是非确定的。然而,现有的模型学习工具只能够学习确定性的 Mealy 机。在实际应用中,我们有时可以通过将不同的具体输出事件抽象为单个抽象输出以消除非确定性,但在许多情况下这是不可能的。Volpato 和 Tretmans 38 提出了一种*L **对非确定性 I / O 自动机的主动学习的调整方案。他们的算法能够学习非确定性 SUL,并且它允许我们构造部分或近似模型。同样,还需要进行大量工作以将这些想法纳入最先进的工具,如 LearnLib、libalf、RALib 或 Tomte。
模型质量。由于模型学习算法生成的模型是通过有限数量的测试获得的,所以我们不能确保它们是正确的。然而,从实践的角度来看,我们希望能够对学习模型的质量进行定量说明,例如,断言假设高概率地近似正确。Angluin 6 根据 Valiant 的 PAC 学习方法提出了这样的一种设定。她的想法是假设在输入字母表 I 上一组单词的一些(未知)概率分布。为了测试假设,一致性测试器(参见图 4)选择指定数量的输入词(这些是统计独立的事件),并检查每个词,无论 SUL 的输出结果是否和假设相一致。只有当完全一致时,一致性测试仪才会向 learner 返回答案'yes'。如果选择一个字符串所表现出来的差异的概率最多为ε,则该假设被认为是 SUL 的ε近似。给定 SUL 的状态数量的界限以及两个常数ε和δ,Angluin 的多项式算法产生模型,使得该模型是 SUL 的近似的概率为至少 1 -δ。Angluin 的结果是优雅的,但在反应系统的设置中不现实,因为我们通常在输入词上没有固定的分布。(输入受 SUL 环境的控制,且此环境可能会发生改变。)
我们使用传统一致性测试,可以设计出一个测试套件,该测试套件可在给定 SUL 状态数量上限的情况下保证学习模型的准确性。但是这种方法也不能令人满意,因为所需要的测试序列的数量会随着 SUL 的状态数量呈现指数型增长。因此,挑战在于如何在 Angluin 方法和传统的一致性测试之间建立一个折中。系统日志通常提供了一个输入词集合的概率分布,该输入词集合可被用来作为定义某个度量标准的启动点。
打开箱子。使用黑箱模型学习技术可以有很多原因。例如,我们可能想要了解组件的行为,但是不能访问代码。或者我们可以访问代码,但没有合适的工具来分析它(例如,在旧版软件的情况下)。即使在「白箱」情况下,我们可以访问代码并有强大的代码分析工具,黑箱学习也是有意义的,例如因为黑箱模型可以用于生成回归测试,用于检查是标准是否一致,或作为更大的基于模型开发的系统的一部分。一个重要的研究挑战是结合黑箱和白箱模型提取技术,例如,使用白盒方法,如静态分析和 concolic 测试,以帮助回答由黑箱 learner 提出的等价性查询。
致谢。部分工作是在 STW 项目 11763(ITALIA)和 13859(SUMBAT)以及 NWO 项目 628.001.009(LEMMA)和 612.001.216(ALSEP)的背景下进行的。
参考文献:
1. Aarts, F., Fiterău-Broştean, P., Kuppens, H., Vaandrager, F. Learning register automata with fresh value generation. In ICTAC'15, LNCS 9399 (2015). Springer, 165–183.
2. Aarts, F., Jonsson, B., Uijen, J., Vaandrager, F. Generating models of infinite-state communication protocols using regular inference with abstraction. Formal Methods Syst. Des. 46, 1 (2015), 1–41.
3. Aarts, F., de Ruiter, J., Poll, E. Formal models of bank cards for free. In SECTEST'13 (2013). IEEE, 461–468.
4. Aarts, F., Vaandrager, F. Learning I/O automata. In CONCUR'10, LNCS 6269 (2010). Springer, 71–85.
5. Alur, R., Madhusudan, P. Visibly pushdown languages. In STOC'04 (2004). ACM, 202–211.
6. Angluin, D. Learning regular sets from queries and counterexamples. Inf. Comput. 75, 2 (1987), 87–106.
7. Bennett, K. Legacy systems: coping with success. IEEE Softw. 12, 1 (1995), 19–23.
8. Berg, T., Grinchtein, O., Jonsson, B., Leucker, M., Raffelt, H., Steffen, B. On the correspondence between conformance testing and regular inference. In FASE'05, LNCS 3442 (2005). Springer, 175–189.
9. Bollig, B., Katoen, J.-P., Kern, C., Leucker, M., Neider, D., Piegdon, D. libalf: The automata learning framework. In CAV'10, LNCS 6174 (2010). Springer, 360–364.
10. Cassel, S., Howar, F., Jonsson, B. RALib: A LearnLib extension for inferring EFSMs. In DIFTS 15 (2015).
11. Cassel, S., Howar, F., Jonsson, B., Merten, M., Steffen, B. A succinct canonical register automaton model. J. Log. Algebr. Meth. Program. 84, 1 (2015), 54–66.
12. Cassel, S., Howar, F., Jonsson, B., Steffen, B. Active learning for extended finite state machines. Formal Asp. Comput. 28, 2 (2016), 233–263.
13. Chalupar, G., Peherstorfer, S., Poll, E., Ruiter, J. Automated reverse engineering using Lego. In WOOT'14 (Aug. 2014). IEEE Computer Society.
14. Cho, C., Babic, D., Shin, E., Song, D. Inference and analysis of formal models of botnet command and control protocols. In CCS'10 (2010). ACM, 426–439.
15. Clarke, E., Grumberg, O., Peled, D. Model Checking. MIT Press, Cambridge, MA, 1999.
16. Feng, L., Lundmark, S., Meinke, K., Niu, F., Sindhu, M., Wong, P. Case studies in learning-based testing. In ICTSS'13, LNCS 8254 (2013). Springer, 164–179.
17. Fiterău-Broştean, P., Janssen, R., Vaandrager, F. Combining model learning and model checking to analyze TCP implementations. In CAV'16, LNCS 9780 (2016). Springer, 454–471.
18. Grinchtein, O., Jonsson, B., Leucker, M. Learning of event-recording automata. Theor. Comput. Sci. 411, 47 (2010), 4029–4054.
19. Groce, A., Peled, D., Yannakakis, M. Adaptive model checking. Logic J. IGPL 14, 5 (2006), 729–744.
20. Hagerer, A., Hungar, H., Niese, O., Steffen, B. Model generation by moderated regular extrapolation. In FASE'02, LNCS 2306 (2002). Springer, 80–95.
21. Henrix, M. Performance improvement in automata learning. Master thesis, Radboud University (2015).
22. Hungar, H., Niese, O., Steffen, B. Domain-specific optimization in automata learning. In CAV 2003, LNCS 2725 (2003). Springer, 315–327.
23. de la Higuera, C. Grammatical Inference: Learning Automata and Grammars. Cambridge University Press, 2010.
24. Isberner, M. Foundations of active automata learning: An algorithmic perspective. PhD thesis, Technical University of Dortmund (2015).
25. Isberner, M., Howar, F., Steffen, B. The TTT algorithm: A redundancy-free approach to active automata learning. In RV'14, LNCS 8734 (2014). Springer, 307–322.
26. Isberner, M., Howar, F., Steffen, B. The open-source LearnLib - A framework for active automata learning. In CAV'15, LNCS 9206 (2015). Springer, 487–495.
27. Jhala, R., Majumdar, R. Software model checking. ACM Comput. Surv. 41, 4 (Oct. 2009), 21:1–21:54.
28. Kearns, M.J., Vazirani, U.V. An Introduction to Computational Learning Theory. MIT Press, 1994.
29. Lee, D., Yannakakis, M. Principles and methods of testing finite state machines—A survey. Proc. IEEE 84, 8 (1996), 1090–1123.
30. Margaria, T., Niese, O., Raffelt, H., Steffen, B. Efficient test-based model generation for legacy reactive systems. In HLDVT'04 (2004). IEEE Computer Society, 95–100.
31. Moore, E. Gedanken-experiments on sequential machines. In Automata Studies, Annals of Mathematics Studies 34 (1956). Princeton University Press, 129–153.
32. Peled, D., Vardi, M., Yannakakis, M. Black box checking. J. Autom. Lang. Comb. 7, 2 (2002), 225–246.
33. Rivest, R.L., Schapire, R.E. Inference of finite automata using homing sequences. Inf. Comput. 103, 2 (1993), 299–347.
34. de Ruiter, J., Poll, E. Protocol state fuzzing of TLS implementations. In USENIX Security'15 (2015). USENIX Association, 193–206.
35. Schuts, M., Hooman, J., Vaandrager, F. Refactoring of legacy software using model learning and equivalence checking: an industrial experience report. In iFM'16, LNCS 9681 (2016). Springer, 311–325.
36. Shahbaz, M., Groz, R. Analysis and testing of black-box component-based systems by inferring partial models. Softw. Test. Verif. Reliab. 24, 4 (2014), 253–288.
37. Valiant, L.G. A theory of the learnable. In STOC'84 (1984). ACM, 436–445.
38. Volpato, M., Tretmans, J. Approximate active learning of nondeterministic input output transition systems. Electron. Commun. EASST 72 (2015).
39. Windmüller, S., Neubauer, J., Steffen, B., Howar, F., Bauer, O. Active continuous quality control. In CBSE'13 (2013). ACM, 111–120.
原文链接:http://cacm.acm.org/magazines/2017/2/212445-model-learning/fulltext#F7